MY-ASSIGNMENTEXPERT™可以为您提供 utexas.edu CS167 Cryptography密码学的代写代考和辅导服务!
这是德克萨斯州大学奥斯汀分校密码学课程的代写成功案例。
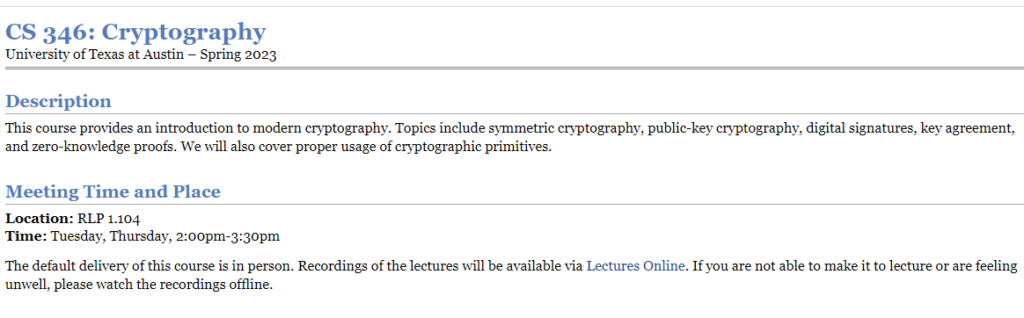
CS346课程简介
This course provides an introduction to modern cryptography. Topics include symmetric cryptography, public-key cryptography, digital signatures, key agreement, and zero-knowledge proofs. We will also cover proper usage of cryptographic primitives.
Location: RLP 1.104
Time: Tuesday, Thursday, 2:00pm-3:30pm
The default delivery of this course is in person. Recordings of the lectures will be available via Lectures Online. If you are not able to make it to lecture or are feeling unwell, please watch the recordings offline.
Prerequisites
Canvas: We will use Canvas, which includes links to Ed Discussion (for announcements and class discussions and Gradescope for assignment submission and grading.
Ed Discussion: We will use Ed Discussion for class discussions and for sending out course announcements. If you have a question about the course material or course logistics, please post it on Ed Discussion instead of emailing the course staff directly. You should be automatically added to the Ed Discussion site via Canvas once the semester starts.
Lectures Online: Recordings of the lectures will be available via Lectures Online after the lecture (if available). You can also access Lectures Online via Canvas.
Gradescope: Homework submissions will be handled via Gradescope. You should be automatically enrolled in the course via Canvas once the semester starts.
Homework: Please see the Course Organization and Policies page for details on how to format and submit your homeworks as well as the collaboration policy for the course.
CS346 Cryptography HELP(EXAM HELP, ONLINE TUTOR)
Let $e$ be the encryption transformation defined as
$e=$ replace each letter of the plaintext with the letter that is $k$ places to the right in the alphabet, where $k$ is an integer that satisfies $k \in{0,1,2, \ldots, 25}$.
Suppose that $k_e=5$. Compute $C=e($ Montgomery, 5)
Let $d$ be the decryption transformation defined as
$d=$ replace each letter of the ciphertext with the letter that is $k$ places to the left in the alphabet, where $k$ is an integer that satisfies $k \in{0,1,2, \ldots, 25}$.
Suppose that $k_d=12$. Compute $M=d$ (mxsqndm, 12).
Suppose that Alice sends Bob the ciphertext $C=$ ZLUKOLSW using the encryption transformation $e$ of Exercise 1. During transmission, Malice obtains the partial ciphertext ZLUK. Find the value of $k_e$ and $k_d$. What is the plaintext message? What type of attack is Malice engaged in?
Suppose that Malice knows that Alice and Bob are using $e$ and $d$ as in Section 1.1 to communicate securely. Suppose that Malice has obtained the plaintext,ciphertext pairing secret, bnlanc. Explain how Malice can obtain the encryption key $k_e$. What is the value of $k_e$ ?)
Consider the following variation of the cryptosystem given in Section 1.1. In this case, the alphabet is the three-element set of letters ${a, b, c}$, and plaintext messages are finite sequences of $a$ ‘s, $b$ ‘s, and $c$ ‘s. Thus the message space $\mathcal{M}=$ ${a, b, c}^*$. Let $e$ be the encryption transformation defined as
$e=$ replace each letter of the plaintext with the letter that is $k$ places to the right in the alphabet, where $k$ is an integer that satisfies $k \in{0,1,2}$.
Using this cryptosystem, compute the following:
(a) $C=e($ accbbac, 2$)$
(b) $M=d($ abcacbc, 1$)$

MY-ASSIGNMENTEXPERT™可以为您提供 UTEXAS.EDU CS167 CRYPTOGRAPHY密码学的代写代考和辅导服务!