MY-ASSIGNMENTEXPERT™可以为您提供 utexas.edu CS167 Cryptography密码学的代写代考和辅导服务!
这是德克萨斯州大学奥斯汀分校密码学课程的代写成功案例。
CS346课程简介
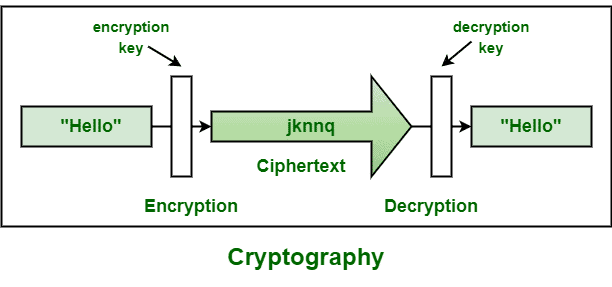
This course provides an introduction to modern cryptography. Topics include symmetric cryptography, public-key cryptography, digital signatures, key agreement, and zero-knowledge proofs. We will also cover proper usage of cryptographic primitives.
Location: RLP 1.104
Time: Tuesday, Thursday, 2:00pm-3:30pm
The default delivery of this course is in person. Recordings of the lectures will be available via Lectures Online. If you are not able to make it to lecture or are feeling unwell, please watch the recordings offline.
Prerequisites
Canvas: We will use Canvas, which includes links to Ed Discussion (for announcements and class discussions and Gradescope for assignment submission and grading.
Ed Discussion: We will use Ed Discussion for class discussions and for sending out course announcements. If you have a question about the course material or course logistics, please post it on Ed Discussion instead of emailing the course staff directly. You should be automatically added to the Ed Discussion site via Canvas once the semester starts.
Lectures Online: Recordings of the lectures will be available via Lectures Online after the lecture (if available). You can also access Lectures Online via Canvas.
Gradescope: Homework submissions will be handled via Gradescope. You should be automatically enrolled in the course via Canvas once the semester starts.
Homework: Please see the Course Organization and Policies page for details on how to format and submit your homeworks as well as the collaboration policy for the course.
CS346 Cryptography HELP(EXAM HELP, ONLINE TUTOR)
(1 point) Which of the following security goal(s) does encryption address : (1) Confidentiality (2) Integrity (3) Sender authentication (4) Non-repudiation.
Solution. Encryption aims to provide confidentiality only.
(1 point) A one-time pad is provably secure. What makes it hard to use in practice?
Solution. One-time pad requires the key length to be same as the message length. The difficulty of setting up a shared key each time users wish to communicate makes it hard to use in practice.
(1 point) Suppose you obtain two ciphertext $C, C^{\prime}$ encrypted using one-time pad, with key $K$ and its bitwise complement $\bar{K}$ respectively. What can you infer about the corresponding plaintext messages?
Solution. You can obtain $m \oplus m^{\prime}$. Note that $\bar{K}=K \oplus 1$, therefore,
$$
\begin{aligned}
& C \oplus C^{\prime} \oplus 1=(m \oplus K) \oplus\left(m^{\prime} \oplus K \oplus 1\right) \oplus(1) \
& =m \oplus m^{\prime} .
\end{aligned}
$$
(5 points) Alice and Bob are using public keys $\left(e_1, N_1\right),\left(e_2, N_2\right)$ respectively. Suppose you are informed that their RSA moduli $N_1, N_2$ are not relatively prime. How would you break the security of their subsequent communication? It is sufficient to show that you can get $\phi\left(N_1\right)$ and $\phi\left(N_2\right)$.
Solution. Since $N_1, N_2$ share a common divisor (they are not relatively prime), let $p$ be the shared prime divisor. Let $N_1=p . q$ and $N_2=p . r$.
$p=G C D\left(N_1, N_2\right)$, which can be computed effeciently using Euclid’s Algorithm. We do not expect the solution to outline the algorithm.
$q=N_1 / p$ and $r=N_2 / p$ can be computed with the knowledge of $p$.
$\phi\left(N_1\right)=(p-1)(q-1)$ and $\phi\left(N_2\right)=(p-1)(r-1)$ can be computed with the knowledge of $p, q, r$.
(5 points) Suppose that a system uses textbook RSA encryption. An attacker wants to decrypt a ciphertext $c$ to obtain the corresponding confidential plaintext $m$. Assume that the victim system readily decrypts arbitrary ciphertexts that the attacker can choose, except for ciphertext $c$ itself. Show that the attacker can obtain $m$ from $c$ even under this setting, i.e a chosen ciphertext attack is possible.
Solution. We know that $c=m^e \bmod N$, i.e, the attacker aims to obtain $m$ from $c$. To do this, the attacker uses the following scheme.
Step 1. The attacker chooses a random number ‘ $r$ ‘ such that $\operatorname{gcd}(r, N)=1$. The attacker encrypts it as using the public key : $C_r=r^e \bmod N$.
Step 2. He computes $C^{\prime}=c . C_r \bmod N$, and asks the system to decrypt $C^{\prime}$. Let the decryption be $M^{\prime}$. By definition of RSA encryption, we know that:
$$
M^{\prime}=\left(C^{\prime}\right)^d \bmod N
$$
It follows that:
$$
\begin{aligned}
& C^{\prime}=\left(\left(m^e \bmod N\right) \cdot\left(r^e \bmod N\right)\right) \bmod N . \
& =(m \cdot r)^e \bmod N
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
& M^{\prime}=C^{\prime d} \bmod N \
& M^{\prime}=(\operatorname{mor})^{e d} \bmod N \
& M^{\prime}=(\operatorname{mor}) \bmod N
\end{aligned}
$$
Step 3. The attacker obtains $M^{\prime}$ and recovers the confidential plaintext $m$ by computing $M^{\prime} \cdot r^{-1} \bmod N$.
$M^{\prime} \cdot r^{-1} \bmod N=\operatorname{mor} \cdot r^{-1} \bmod N$ $=m \bmod N$
Keep in mind that $r$ has to be chosen such that its multiplicative inverse modulo $N$ exists. This is true iff $\operatorname{gcd}(r, N)=1$.

MY-ASSIGNMENTEXPERT™可以为您提供 UTEXAS.EDU CS167 CRYPTOGRAPHY密码学的代写代考和辅导服务!