MY-ASSIGNMENTEXPERT™可以为您提供MEMORIAL CS6917 Complex Networks复杂网络课程的代写代考和辅导服务!
这是纽芬兰纪念大学 复杂网络课程的代写成功案例。
CS6917课程简介
Complex problems emerging from various disciplines and interaction of large amount of data can be modelled with networks. Networks are powerful tools for making sense of the world in the big-data era. The scientific study of networks, including computer networks, social networks, and biological networks, has received an enormous amount of interest recently. The rise of the Internet, the wide availability of inexpensive computers, and penetration of smart mobile devices have made it possible to gather and analyze network data on a large scale, and the development of a variety of new theoretical tools has allowed us to extract new knowledge from many different kinds of networks.
Prerequisites
The study of large, complex networks is broadly interdisciplinary and important developments have occurred in many fields, including mathematics, physics, computer and information sciences, biology, and the social sciences. Subjects covered in this course include the measurement and structure of networks, the fundamentals of network theory, computer algorithms, and spectral methods and mathematical models of networks, all at a much greater scale.
CS6917 Complex Networks HELP(EXAM HELP, ONLINE TUTOR)
Consider a regular graph of $N$ nodes and the degree $k$ ( $k$-regular graph).
A) (2 points) Show that the average path length:
$$
l=\frac{N}{2 k} .
$$
B) (2 points) Show that the clustering coefficient (the average local clustering coefficient):
$$
C=\frac{3(k-2)}{(k-1)}
$$
Time available: 1 hour and $\mathbf{3 0}$ minutes
1) Characterize the structure of the network showed below, using classic metrics. (25 points)
a) What is the number of nodes and edges in this network? (5 points)
Answer: Nodes $=8 ;$ Edges $=12$
b) Explain the concept of density and calculate the graphs’ density. (10 points)
Answer: Density is a metric that varies from 0 to 1 and tells how far apart the actual number of edges is from the possible number of edges.
This graphs’ density is calculated like this: $\mathbf{2 }$ (number of nodes)/(number of edges)(number of edges1) 0.121212..
c) Calculate this networks’ mean degree. (5 points)
Answer: $23 / 8=2.875$
d) Which vertices are the most far apart from each other? What is the longest path? (5 points)
Hint: do not overestimate the path, use always the shortest longest one. For instance: from $B$ to $D$, use $B$ $\gg C \gg D$, instead of $B \gg C \gg A \gg F \gg D$.
Answer: $B$ and $H$. The longest path is $B>>C \gg D$ >> $\mathrm{C}$ > $H$.
2) What is a scale-free network model? Why are those kinds of models important to studies in social networks? Choose two of those models and explain the main difference between them. (25 points)
Answer: A scale-free network model is a graph/network model that allows us to add or remove nodes in the graph with time.
Those kinds of models are important to social networks because they allow dynamism, which is the greatest characteristic of social networks, since the number of people in real networks change every day.
Two models are Preferential Attachment (Barabási and Albert) and Model of Holme and Jun Kim (tunable clustering).
The main difference between those models is the fact that the model with tunable clustering allows us to add steps in the graph that focus on forming triads, while in Barabási and Albert model, triads are formed only eventually and randomly.
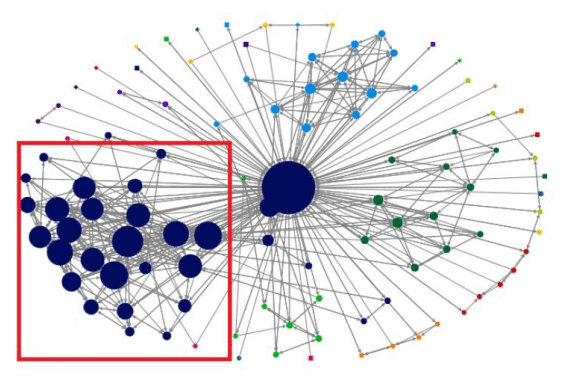
3) Given the ego network snapshot below, the highlighted cluster and the following information, suggest three nodes (ego node does not count) that could potentially reach a large audience broadcasting some kind of information concerning technology to most people in this group. (50 points)
Graph information:
- Most people in this group are Computer Science students and use this network to many purposes, that may or may not be related to technology.
- The size of each node is directly proportional to each nodes’ eigenvector centralities.
- The fact that two nodes are too close from each other in the representation has nothing to do with the kind of interaction they have in the network.
a) What are the three nodes you selected to broadcast information? Why were they chosen? (10 points)
Hint: you can identify those nodes with numbers in the figure.
Hint #2: do not use the ego node in your answer.
Answer: Highlighted nodes 1, 2, 3, since those are the biggest ones in the highlighted area, which means they have the biggest eigenvector centrality and are well-connected nodes in the cluster.
b)What kind of extra information about this network could be useful to help broadcast content about technology? (20 points)
Answer: I am looking for different and possibly creative answers in this question. A few examples of what I would like to see are: number of connections of each node, if those users really care or not about technology in the context of this network, whether this snapshot is updated or not, how much users take each others’ opinions in consideration.
c) What kinds of assumptions do you have to make in order to balance the lack of helpful information and how those assumptions can affect your strategy? ( 20 points)
Answer: Once again, what I am looking for here are creative perspectives, and things learned specially from the topic “problems in social network analysis”. Topics listed in 3-b can be used here with the appropriate explanations. Other perspective I would like to see is taking in consideration if those wellranked users are still active in the network and how they deal with their connections, their areas of interest etc.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。


