MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu MATH4105 General Relativity广义相对论课程的代写代考和辅导服务!
这是昆士兰大学 广义相对论课程的代写成功案例。
MATH4105课程简介
In his book “Space-Time Structure,” Schrodinger says: “In Einstein’s theory of gravitation, matter and its dynamical interaction are based on the notion of an intrinsic geometric structure of the space-time continuum. The ideal aspiration, the ultimate aim, of the theory is not more and not less than this: A four-dimensional continuum endowed with a certain intrinsic geometrical structure, a structure that is subject to certain inherent purely geometrical laws, is to be an adequate model or picture of the ‘real world around us in space and time’ with all that it contains and including its total behaviour, the display of all events going on in it.”
Acceptance of this notion of “geometrizing” all of physics has waxed and waned since Einstein’s and Schrodinger’s time, but the striking achievements of Einstein’s ‘General Theory of relativity’ compel us to study both the theory and the mathematical structure upon which it is founded.
Prerequisites
Accordingly, the first half of the course will introduce the basic mathematical ideas of pseudo-Riemannian geometry: manifolds; tensors; connections; parallel transport; covariant differentiation; geodesics; curvature; differential forms; Bianchi identities; Ricci, Einstein and Weyl tensors.
By working through problems, the student will have the opportunity to acquire a basic working knowledge of these concepts, and should then have the background necessary for the second half of the course.
MATH4105 General Relativity HELP(EXAM HELP, ONLINE TUTOR)
If $a$ is a constant, consider a spacetime with metric
$$
d \tau^2=\mathrm{e}^{-2 a x} d t^2-d x^2-d y^2-d z^2
$$
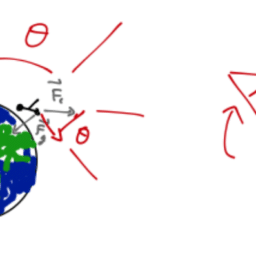
(a) Find all of the nonzero affine connections. (b) Find the geodescic equation for $d^2 x / d \tau^2$ and show that in the limit of instantaneous zero velocity $d x / d t=$ $d y / d t=d z / d t=0$, the acceleration in the $\mathrm{x}$ direction is constant, $d^2 x / d \tau^2=a$, as though the particle were in a uniform gravitational field. (c) Find the components of the Riemann tensor $R_{001}^1, R_{110}^0, R_{010}^1$, and $R_{101}^0$. The other components are zero. (d) From the Einstein Field Equations, find the diagonal elements of the energy momentum tensor. Is this tensor physically acceptable?
In a Schwarzchild metric, what is the volume contained in the spherical shell between radii $r_1$ and $r_2$ ? You may leave your answer as an integral.
Consider two concentric coplanar circles ( $r=$ constant) in Schwarzschild geometry. Suppose that the measured circumferences of these circles are $C_1$ and $C_2$. (a) What is the radial co-ordinate difference $\Delta r$ between these circles? (b) What is the measured radial distance between these two circles? (c) For the sun, take the two circles as having circumferences $C_1=2 \pi R_{\odot}$ and $C_2=4 \pi R_{\odot}$. By how many centimeters does the measured radial distance between them differ from the result expected in flat space?
A particle is to be launched in the outward radial direction from the point $r=4 G M$ in the Schwarzschild geometry. (a) At what speed $d r / d \tau$ must the particle be launched if it is to reach the point $r=8 G M$ with zero speed? (b) How much proper time does this trip take?
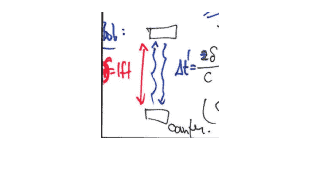
Light orbits a Schwarzschild black hole at a radius $r=3 G M$, where as usual $r$ is the radial co-ordinate in standard co-ordinates. (a) What is the orbital period of the light as measured by a distant observer? (b) What is the orbital period as measured by an observer at rest at $r=3 G M$ ?
Note that
$$
\int \frac{d y}{\sqrt{1-1 / y}}=y \cos \theta-\ln \tan (\theta / 2) \quad \text { where } \quad \theta=\arcsin \left(y^{-1 / 2}\right)
$$

MY-ASSIGNMENTEXPERT™可以为您提供MY.UQ.EDU MATH4105 GENERAL RELATIVITY广义相对论课程的代写代考和辅导服务!