MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu MATH4105 General Relativity广义相对论课程的代写代考和辅导服务!
这是昆士兰大学 广义相对论课程的代写成功案例。
MATH4105课程简介
In his book “Space-Time Structure,” Schrodinger says: “In Einstein’s theory of gravitation, matter and its dynamical interaction are based on the notion of an intrinsic geometric structure of the space-time continuum. The ideal aspiration, the ultimate aim, of the theory is not more and not less than this: A four-dimensional continuum endowed with a certain intrinsic geometrical structure, a structure that is subject to certain inherent purely geometrical laws, is to be an adequate model or picture of the ‘real world around us in space and time’ with all that it contains and including its total behaviour, the display of all events going on in it.”
Acceptance of this notion of “geometrizing” all of physics has waxed and waned since Einstein’s and Schrodinger’s time, but the striking achievements of Einstein’s ‘General Theory of relativity’ compel us to study both the theory and the mathematical structure upon which it is founded.
Prerequisites
Accordingly, the first half of the course will introduce the basic mathematical ideas of pseudo-Riemannian geometry: manifolds; tensors; connections; parallel transport; covariant differentiation; geodesics; curvature; differential forms; Bianchi identities; Ricci, Einstein and Weyl tensors.
By working through problems, the student will have the opportunity to acquire a basic working knowledge of these concepts, and should then have the background necessary for the second half of the course.
MATH4105 General Relativity HELP(EXAM HELP, ONLINE TUTOR)
Lorentz contraction exercise from Brandenberger
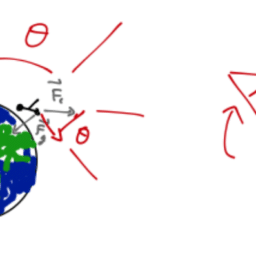
(a) Suppose frame $S^{\prime}$ moves with velocity $v$ relative to frame $S$. A projectile in frame $S^{\prime}$ is fired with velocity $v^{\prime}$ at an angle $\theta^{\prime}$ with respect to the forward direction of motion $(\vec{v})$. What is this angle $\theta$ measured in $S$ ? What if the projectile is a photon?
An (un-normalized) velocity 4 -vector for the projectile in frame $S^{\prime}$ is
$$
v^{\prime} \propto\left(\begin{array}{c}
\mathrm{d} t^{\prime} \
\mathrm{d} x_1^{\prime} \
\mathrm{d} x_2^{\prime} \
\mathrm{d} x_3^{\prime}
\end{array}\right) \propto\left(\begin{array}{c}
1 \
v^{\prime} \cos \theta^{\prime} \
v^{\prime} \sin \theta^{\prime} \
0
\end{array}\right)
$$
(The normalization doesn’t matter because we can determine angles by taking ratios of components.) This is related to the velocity 4-vector for the projectile seen in frame $S$ by the Lorentz boost :
$$
\begin{gathered}
v=\left(\begin{array}{cccc}
\gamma & v \gamma & 0 & 0 \
v \gamma & \gamma & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1
\end{array}\right) v^{\prime}=\left(\begin{array}{c}
\gamma\left(1+v^{\prime} \cos \theta^{\prime} v\right) \
\gamma\left(v+v^{\prime} \cos \theta^{\prime}\right) \
v^{\prime} \sin \theta^{\prime} \
0
\end{array}\right) \
\tan \theta=\frac{\mathrm{d} x_2 / \mathrm{d} t}{\mathrm{~d} x_1 / \mathrm{d} t}=\frac{\mathrm{d} x_2}{\mathrm{~d} x_1}=\frac{v^{\prime} \sin \theta^{\prime}}{\gamma\left(v+v^{\prime} \cos \theta^{\prime}\right)}
\end{gathered}
$$
$$
\gamma=\frac{1}{\sqrt{1-v^2}}
$$
If the projectile is a photon, $v^{\prime}=1$. In this case
$$
\tan \theta=\frac{\sin \theta^{\prime}}{\gamma\left(v+\cos \theta^{\prime}\right)} .
$$
This formula leads to the notion of the apparent velocity of an object, which can actually be larger than $c$ and which is observed in the study of high-energy astrophysical objects like active galactic nuclei.
(b) An observer $A$ at rest relative to the fixed distant stars sees an isotropic distribution of stars in a galaxy which occupies some region of her sky. The number of stars seen within an element of solid angle $\mathrm{d} \Omega$ is
$$
P \mathrm{~d} \Omega=\frac{N}{4 \pi} \mathrm{d} \Omega
$$
where $N$ is the total number of stars that $A$ can see. Another observer $B$ moves uniformly along the $z$ axis relative to $A$ with velocity $v$. Letting $\theta^{\prime}$ and $\varphi^{\prime}$ be respectively the polar (with respect to $\hat{z}$ ) and azimuthal angle in the inertial frame of $B$, what is the distribution function $P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right)$ such that $P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right) \mathrm{d} \Omega^{\prime}$ is the number of stars seen by $B$ in the solid angle $\mathrm{d} \Omega^{\prime}=\sin \theta^{\prime} \mathrm{d} \theta^{\prime} \mathrm{d} \varphi^{\prime}$.
$\varphi^{\prime}=\varphi$, since the $z$ axes are aligned. From the previous part of the problem, the relevant projectiles are photons, so the angles are related by
$$
\tan \theta=\frac{\sin \theta^{\prime}}{\gamma\left(v+\cos \theta^{\prime}\right)}
$$
Since the total number of stars is the same, and the limits of integration are the same $\left(\theta=0 \Longrightarrow \theta^{\prime}=0, \theta=\pi \Longrightarrow \theta^{\prime}=\pi\right)$, we have
$$
N=\int_0^{2 \pi} \mathrm{d} \varphi^{\prime} \int_0^\pi \mathrm{d} \theta^{\prime} \sin \theta^{\prime} \cdot P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right)=\int_0^{2 \pi} \mathrm{d} \varphi \int_0^\pi \mathrm{d} \theta \sin \theta \cdot P(\theta, \varphi) .
$$
A more refined and also true statement is that the number of stars in any solid angle is the same in the two frames:
$$
P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right) \sin \theta^{\prime} \mathrm{d} \theta^{\prime}=P(\theta, \varphi) \sin \theta \mathrm{d} \theta=\frac{N}{4 \pi} \sin \theta \mathrm{d} \theta .
$$
Here we used the fact that the azimuthal angles are the same, and in the last step we used the ‘isotropic’ datum. Now we have to have a little chain rule party to find
$$
P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right)=\frac{N}{4 \pi} \frac{\mathrm{d} \theta}{\mathrm{d} \theta^{\prime}} \frac{\sin \theta}{\sin \theta^{\prime}}
$$
as a function of $\theta^{\prime}$. One way to do this is to solve (8) for $\cos \theta$ and differentiate with respect to $\theta$. Notice that we need to take a square root at some point and continuity and correctness demands that we choose $\cos \theta= \pm \frac{1}{\sqrt{1+\tan ^2 \theta}}$ with the for $\pi / 2<\theta<\pi$ and the + for $0<\theta<\pi / 2$. But, remarkably, this relation can be simplified to
$$
\cos \theta=\frac{v+\cos \theta^{\prime}}{1+v \cos \theta^{\prime}}
$$
Now this is a relation of the form $y=\frac{v+x}{1+v x}$ and we want
$$
\frac{\sin \theta \mathrm{d} \theta}{\sin \theta^{\prime} \mathrm{d} \theta^{\prime}}=\frac{\mathrm{d} \cos \theta}{\mathrm{d} \cos \theta^{\prime}}=\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{1-v^2}{\left(1+v \cos \theta^{\prime}\right)^2}
$$
This leads to
$$
P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right)=\frac{N}{4 \pi} \frac{1}{\gamma^2} \frac{1}{\left(1+v \cos \theta^{\prime}\right)^2}
$$
An uglier but also correct expression is:
$$
P^{\prime}\left(\theta^{\prime}, \varphi^{\prime}\right)=\frac{N}{4 \pi}\left|\left(1+\left(\frac{\sin ^2 \theta^{\prime}}{\gamma^2\left(v+\cos \theta^{\prime}\right)^2}\right)\right)^{-3 / 2} \frac{v \cos \theta^{\prime}+1}{\gamma^2\left(v+\cos \theta^{\prime}\right)^3}\right| .
$$
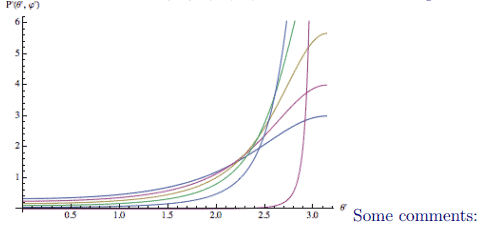
The results for $v=.5, .6, .7, .8, .9, .99$ are shown in the figure:
(1) We can’t just transform the spatial bits using Lorentz contraction (like $\mathrm{d} z=$ $\gamma \mathrm{d} z^{\prime}$ ) for the following reason: unless we also account for the transformation in the time coordinates, observers in the two frames won’t both see the light rays moving at the speed of light!
The light that the observer at rest sees at a given moment was at a spherical shell of radius ct a time $t$ ago:
$$
\left{x, y, z \mid x^2+y^2+z^2=c^2 t^2\right}
$$
The light seen simultaneously by the moving observer was not at the same set of points. (2) Note that the light is also Doppler shifted, so that the light at $\theta \in(0, \pi / 2)$ is blueshifted and at $\theta \in(\pi / 2, \pi)$ is redshifted.
that is: the angle between the photon’s velocity and the forward direction of the observer is actually $\pi-\theta $ and the identity $\cos (\pi-\theta)=-\cos (\theta)$ shows that the stars all look like they are in the forward direction. The fact that the light all smushes down to the forward axis can be rationalized as follows: if we’re moving at speed $c$, only if we’re heading right at a photon will we run into it – and no matter how fast we go we’ll for sure run into the photons that we’re going to collide with head-on.

MY-ASSIGNMENTEXPERT™可以为您提供MY.UQ.EDU MATH4105 GENERAL RELATIVITY广义相对论课程的代写代考和辅导服务!