计算机代写|CS1699 Deep Learning

In this first exercise, we will implement a simple neuron, or perceptron, as visualized below. We will have just three inputs and one output neuron (we will skip the bias for now). Notice how the perceptron just performs a sum of the individual inputs multiplied by the corresponding weights mapped through an activation function $f(\cdot)$. This can also be expressed as a dot product of the weight vector $\mathbf{W}$ and the input vector $\mathbf{x}$. Thus: $\hat{y}=f\left(\mathbf{W}^T \mathbf{x}\right)$.
In this first part we will implement the perpetron by using numpy library.
import numpy as np

Training data
Let’s consider a very simple dataset. The dataset is composed of the inputs value $x \in \mathbb{R}^3$ and the desired target values. Below, each row is a single example: the first three columns the input and the last column the target output.
$$
\begin{array}{llll}
0 & 0 & 1 & 0 \
0 & 1 & 1 & 0 \
1 & 0 & 1 & 1 \
1 & 1 & 1 & 1
\end{array}
$$
Note that our target outputs are equal to the first column of the input. Therefore the task that the model should learn is very simple. We will see if it can learn that just from the data.
Now let’s define the $x$ and $y$ matrices.
H Our input data is a matrix, each row is one input 5 ample $X=\mathrm{np} \cdot \operatorname{array}([[0,0,1]$,
$$
[0,1,1]
$$
$$
\begin{aligned}
& {[1,0,1] \text {, }} \
& [1,1,1]))
\end{aligned}
$$
H The target output as a colum vector in $2-D$ array format (. $T$ means transpose) $\mathrm{y}=\mathrm{np} \cdot \operatorname{array}([[0,0,1,1]]) \cdot \mathrm{T}$
$\operatorname{print}(‘ \mathrm{X}=, \mathrm{X})$
$\operatorname{print}\left(y^{\prime}=, y\right)$
$X=\left[\begin{array}{lll}0 & 0 & 1\end{array}\right]$
$\left[\begin{array}{lll}0 & 1 & 1\end{array}\right]$
$\left[\begin{array}{lll}1 & 0 & 1\end{array}\right]$
$\left.\left[\begin{array}{lll}1 & 1 & 1\end{array}\right]\right]$
$y=[0]$
[0]
[1]
[1] ]

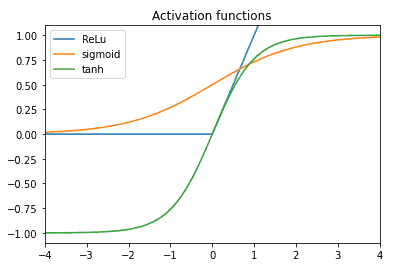
As we said before, in order to define a perceptro we need to define the activation function $f(\cdot)$. There are many possibile activation function that can be use. Let’s plot some commonly used activation functions.

In this particular case we will use the sigmoid function. So, let’s define $f(\cdot)$ as the sigmoid function
$$
\sigma(x)=\frac{1}{1+\exp ^{-x}}
$$
$\operatorname{def} f(x)$
return $1 /(1+\mathrm{np} \cdot \exp (-x))$
Weight initialization
We have to initialise our weights. Let’s initialize them randomly, so that their mean is zero. The weights matrix map the input space into the output space, therefore in our case $\mathbf{W} \in \mathbb{R}^{3 \times 1}$
np.random. seed $([42])$
Hinitialize weights ramdom $l y$ with mean $\theta$
$W=2 * n p . r a n d o m$. random $((3,1))-1$
print $(W=’, W)$
$W=[[0.2788536]$
$[-0.94997849]$
$[-0.44994136]]$

Forward propagation
Now let’s try one round of forward propagation. This means taking an input sample and moving it forward through the network, finally calculating the output of the network.
For our single neuron this is simply $\hat{\mathbf{y}}=f\left(\mathbf{W}^T \mathbf{x}\right)$, where $\mathbf{x}$ is one input vector.
each input sample is arranged as a row of the matrix $X$, therefore we can access the first row by $X[\theta]$. Let’s store it in the variable $X \theta$ for easier access. We’ll use reshape to make sure it’s expressed as a column vector.
$X 0=n p$. reshape $(X[0],(3,1))$
print $(x 0)$
$[[0]$
$[0]$
$[1]]$
The output $\hat{y}$ for the first input can be calculated according to the formula given above
$$
\begin{aligned}
& y_{-} \text {out }=f(n p \cdot \operatorname{dot}(W . T, X 0)) \
& \text { print (‘y_out=’, } \left.y_{-} \text {out }\right) \
& y_{-} \text {out }=[[0.38937471]]
\end{aligned}
$$
the target result is stored in $y[\theta]$. If you check back, you can see we defined it to be 0 . You can see that our network is pretty far away from the right answer. This is why we need to backpropagate the error, to adjust the weights in the right direction.