MY-ASSIGNMENTEXPERT™可以为您提供cs.pitt.edu CS1699 Deep Learning深度学习课程的代写代考和辅导服务!
这是匹兹堡大学 深度学习课程代写成功案例。

CS1699课程简介
Location: Public Health G23
Time: Tuesday and Thursday, 3pm-4:15pm
Instructor: Adriana Kovashka (email: kovashka AT cs DOT pitt DOT edu; use “CS1699” at the beginning of the subject line)
Office: Sennott Square 5325
Office hours: Tuesday 12:20pm-1:30pm and 4:20pm-5:30pm; Thursday 10am-10:50am and 4:20pm-5:30pm
TA: Mingda Zhang (email: mzhang AT cs DOT pitt DOT edu; use “CS1699” at the beginning of the subject line)
TA’s office hours: Tuesday 9am-10am, Wednesday 10am-11am, Thursday 11:30am-12:30pm
TA’s office: Sennott Square 5503
Prerequisites: Math 220 (Calculus I), Math 280 or 1180 (Linear Algebra), CS 1501 (Algorithm Implementation)
Piazza: Sign up for it here. Please use Piazza rather than email so everyone can benefit from the discussion– you can post in such a way that only the instructor sees your name. Please try to answer each others’ questions whenever possible. The best time to ask the instructor or TA questions is during office hours.
Programming language/framework: We will use Python, NumPy/SciPy, and PyTorch.
Prerequisites
Overview
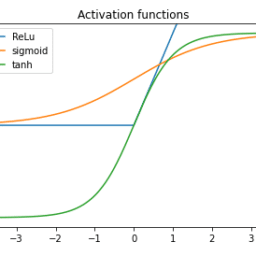
Course description: This course will cover the basics of modern deep neural networks. The first part of the course will introduce neural network architectures, activation functions, and operations. It will present different loss functions and describe how training is performed via backpropagation. In the second part, the course will describe specific types of neural networks, e.g. convolutional, recurrent, and graph networks, as well as their applications in computer vision and natural language processing. The course will also briefly discuss reinforcement learning and unsupervised learning, in the context of neural networks. In addition to attending lectures and completing bi-weekly homework assignments, students will also carry out and present a project.
CS1699 Deep Learning HELP(EXAM HELP, ONLINE TUTOR)
For some $w_* \in \mathbb{R}^d$, the distribution $D_{w_}$ is over pairs $(x, y) \in \mathbb{R}^{d+1}$ such that $x \sim N\left(0, I_d\right)$ and $y=\left\langle x, w_\right\rangle+N(0,1)$.
We are considering the regression task, in which we are given $n$ samples $S=\left{\left(x_1, y_1\right), \ldots,\left(x_n, y_n\right)\right}$ drawn independently from $D_{w_}$, and our goal is to find a function $f: \mathbb{R}^d \rightarrow \mathbb{R}$ that minimizes $\mathbb{E}{(x, y) \sim D{w_}}\left[(f(x)-y)^2\right]$. We define this quantity as $\mathcal{L}(f)$.
(Generalization bound). Let $\mathcal{F}$ be a finite set of bounded functions mapping $\mathbb{R}^d$ to $[-B, B]$, for some constant $B>0$. Prove that with probability at least 0.01 over the choice of $S$,
$$
\max {f \in \mathcal{F}}\left|\mathcal{L}(f)-\frac{1}{n} \sum{(x, y) \in S}(f(x)-y)^2\right| \leq O\left(\sqrt{\frac{\log |\mathcal{F}|}{n}}\right)
$$
Hint. See link. We will also accept solutions that are poly-log $(n)$ loose in the bound above.
(Optimization). In this question we consider the under-parameterized setting where $n \gg d$. Let $\mathcal{F}$ be the set $\left{f_w: w \in \mathbb{R}^{d+1}\right}$ where $f_w(x)=\langle w, x\rangle$. Assume $\left|w_*\right|^2=d$, and consider the stochastic gradient descent algorithm on $\mathcal{L}$. For $(x, y)$ and function $f: \mathbb{R}^d \rightarrow \mathbb{R}$, we define $\mathcal{L}_{x, y}(f)=(f(x)-y)^2$, and consider the following algorithm, where $\delta, \eta$ are hyperparameters:
- Let $w_0 \sim N\left(0, \delta \cdot I_d\right)$.
- For $t=0,2, \ldots, n-1$ do the following:
- Let $(x, y) \sim D_w$.
- Let $w_{t+1}=w_t-\eta \nabla_w \mathcal{L}{(x, y)}\left(f{w_t}\right)$
Prove that, in expectation, this algorithm makes progress towards the optimal solution in every iteration. Specifically, prove that there exists some constant $c \in \mathcal{R}$ such that, for any $t$ :
$$
E\left[\nabla_w L_{\left(x_t, y_t\right)}\left(f_{w_t}\right)\right]=c\left(w_t-w_*\right)
$$
It is possible to use this fact to prove that, in this particular setting, SGD converges to the optimal solution with high probability.
(Inductive bias). In this question we consider the over parameterized setting where $n \ll d$. We show that in this case gradient descent has a certain bias toward low-norm solutions. Specifically, consider the algorithm above.
Prove that in all steps of stochastic gradient descent above, we maintain the invariant that $w_t \in$ $\operatorname{Span}\left(w_0, x_0, \ldots, x_{t-1}\right)$ where $\left(x_i, y_i\right)$ is the sample drawn in step $i$.
Let $S$ be some set $\left{\left(x_0, y_0\right), \ldots,\left(x_{n-1}, y_{n-1}\right)\right}$ in $\mathbb{R}^d$ in “general position” ( $\left|x_i\right|^2 \approx d$ for all $i$, $\left\langle x_i, x_j\right\rangle^2=o(\sqrt{d})$ for all $\left.i \neq j,\left|y_i\right|^2=O(1)\right)$ and let $w_0=0$. Suppose that we run the algorithm on $S$ and that it successfully converges, i.e. $\forall i \leq n,\left\langle x_i, w_n\right\rangle=y_i$. Prove that $w_n$ is
Thus, among all possible “interpolating solutions” to the training set, the algorithm chooses the one that is smallest in $L_2$ norm.
(Toy image search engine). Complex classical algorithms often depend on elementary algorithms with well-known properties – think binary search and quicksort – as subroutines. Analogously, state-of-theart machine learning (ML) pipelines are often built with combinations of “soft” pretrained machine learning primitives. Developing a familiarity with the rapidly expanding toolkit of these ML “building blocks” will make it easier to read new ML papers and design ML solutions of your own.
Over the past couple of years, OpenAI’s CLIP has become a popular primitive for a wide range of imagerelated tasks. In this exercise, we will use CLIP to build a simple text-to-image search tool.

MY-ASSIGNMENTEXPERT™可以为您提供CS.PITT.EDU CS1699 DEEP LEARNING深度学习课程的代写代考和辅导服务