MY-ASSIGNMENTEXPERT™可以为您提供catalog.usf.edu EEL6029 Statistical Inference统计推断的代写代考和辅导服务!
这是南佛罗里达州大学统计推断课程的代写成功案例。

EEL6029 课程简介
Credit Hours: 3
This first-tier graduate course aims at establishing the background in mathematical statistics, and abstract modeling of complex cyber systems, data analytics, and Bayesian intelligence for graduate students in electrical and systems engineering.
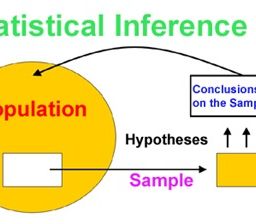
Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability.Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
Prerequisites
Statistical inference makes propositions about a population, using data drawn from the population with some form of sampling. Given a hypothesis about a population, for which we wish to draw inferences, statistical inference consists of (first) selecting a statistical model of the process that generates the data and (second) deducing propositions from the model.
Konishi & Kitagawa state, “The majority of the problems in statistical inference can be considered to be problems related to statistical modeling”. Relatedly, Sir David Cox has said, “How the translation from subject-matter problem to statistical model is done is often the most critical part of an analysis”
EEL6029 Statistical Inference HELP(EXAM HELP, ONLINE TUTOR)
(10 points) Let $\left(X_1, \cdots, X_n\right)$ be a sample from $N\left(\mu, \sigma^2\right)$.
(a). (5 points) If $\sigma^2$ is known, find a minimum value for $n$ to guarantee that a 0.95 confidence interval for $\mu$ will have length no more than $\sigma / 4$.
(b). (5 points) If $\sigma^2$ is unknown, find a minimum value for $n$ to guarantee that a 0.95 confidence interval for $\mu$ will have length no more than $\sigma / 4$.
(15 points) Let $X_1, \cdots, X_n$ be a sample from $U(0, \theta)$, and let $T(\mathbf{X}):=X_{(n)}$ be the largest order statistic. Prove that $T / \theta$ is a pivotal quantity and show that the interval
$$
\left{\theta: T(\mathbf{x}) \leq \theta \leq \frac{T(\mathbf{x})}{\alpha^{1 / n}}\right}
$$
is the shortest $1-\alpha$ pivotal interval.
(20 points) Let $\left(X_1, \cdots, X_n\right)$ be independent random variables with pdfs
$$
f_{X_i}(x \mid \theta)=\exp (i \theta-x) I_{[i \theta, \infty)}(x)
$$
where $\mathbb{I}_{[i \theta, \infty)}(x)$ is an indicator function. Prove that $T=\min _i\left(X_i / i\right)$ is a sufficient statistic for $\theta$. Based on $T$, find the $1-\alpha$ confidence interval for $\theta$ of the form $[T+a, T+b]$ which is of minimum length.
in this problem, you do not need to explain your answer) Express $p_i$ (the probability of having $X=x_i$ in terms of cdf cumulative distribution function
Introduce a function $M(a)=E\left[(X-a)^2\right]$. (a) Express this function through var and $\mu$ (the mean). (b) Prove that this function takes the minimal value at $a=\mu$. (c) Find the minimum of $M$.
Derive the formula $\sum_{m=0}^n\left(\begin{array}{c}n \ m\end{array}\right)=2^n$ from the binomial probability
$$
\operatorname{Pr}(X=m)=\left(\begin{array}{c}
n \
m
\end{array}\right) p^m(1-p)^{n-m}
$$

MY-ASSIGNMENTEXPERT™可以为您提供CATALOG.USF.EDU EEL6029 STATISTICAL INFERENCE统计推断的代写代考和辅导服务!