MY-ASSIGNMENTEXPERT™可以为您提供cuhk.edu.hk ENGG5501 Convex Optimization凸优化课程的代写代考和辅导服务!
这是香港中文大学凸优化课程的代写成功案例。
ENGG5501课程简介
Announcements
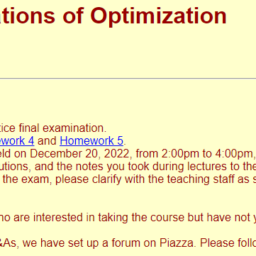
NEW: Here is the solution to the practice final examination.
NEW: Here are the solutions to Homework 4 and Homework 5.
NEW: The final examination will be held on December 20, 2022, from 2:00pm to 4:00pm, in ERB LT. You can bring the course handouts, homeworks, homework solutions, and the notes you took during lectures to the exam. No other material will be allowed. If you have questions about the rules of the exam, please clarify with the teaching staff as soon as possible.
Prerequisites
Here is the midterm solution.
Welcome to ENGG 5501! Students who are interested in taking the course but have not yet registered (or are not able to register) should contact the course instructor.
To better facilitate discussions and Q&As, we have set up a forum on Piazza. Please follow this link to sign up.
ENGG5501 Convex Optimization HELP(EXAM HELP, ONLINE TUTOR)
Consider the following primal and dual pair of linear optimization problems.
$$
\begin{aligned}
\operatorname{minimize}{x \in \mathbb{R}^n} & c^{\top} x \ \text { subject to } & A x=b, x \geq 0, \end{aligned} $$ and $$ \begin{aligned} \operatorname{minimize}{y \in \mathbb{R}^m} & -b^{\top} y \
\text { subject to } & A^{\top} y \leq c .
\end{aligned}
$$
Show that if $x^$ and $y^$ are the respective optimal solutions, then
$$
\left(x^\right)^{\top}\left[A^{\top} y^-c\right]=0
$$
In other words, whenever $x_i^* \neq 0$, the $i$-th constraint in $A^{\top} y \leq c$ holds with equality. This property is known as the complementaty slackness condition.
Consider the following linear optimization problem:
$$
\begin{aligned}
\text { minimize }_{x \in \mathbb{R}^4} & x_1+5 x_2+2 x_3+13 x_4 \
\text { subject to } & 5 x_1-6 x_2+4 x_3-2 x_4=0, \
& x_1-x_2+6 x_3+9 x_4=16, \
& x_1, x_2, x_3, x_4 \geq 0 .
\end{aligned}
$$
Find the dual of the above optimization problem. Suppose $x_1=0, x_2=2, x_3=3$, and $x_4=0$ is the optimal solution of the above problem. Following complementarity slackness condition, find the optimal dual solution and show that strong duality holds. Verify your answer using CVX/YALMIP.
Consider the following linear optimization problem:
$$
\begin{array}{rl}
\text { maximize }_{x \in \mathbb{R}^2} & 5 x_1+10 x_2 \
\text { subject to } & x_1+3 x_2 \leq 50, \
& 4 x_1+2 x_2 \leq 60, \
& x_1 \leq 5 \
& x_1, x_2 \geq 0 .
\end{array}
$$
Find the dual of the above optimization problem. Suppose $x_1=5, x_2=15$ is the optimal solution of the above problem. Following complementarity slackness condition, find the optimal dual solution and show that strong duality holds. Verify your answer using CVX/YALMIP.
Consider the convex optimization problem:
$$
\begin{aligned}
\min _{x \in \mathbb{R}^n} & f_0(x) \
\text { s.t. } & f_i(x) \leq 0, \quad i \in[m] .
\end{aligned}
$$
Let there exist $x^$ and $\lambda^$ that satisfy the KKT conditions for this problem. Then, show that
$$
\nabla f\left(x^\right)^{\top}\left(x-x^\right) \geq 0
$$
for all feasible $x$. This shows the equivalence between the general optimality condition derived in class and the KKT conditions derived in the context of duality.

MY-ASSIGNMENTEXPERT™可以为您提供CUHK.EDU.HK ENGG5501 CONVEX OPTIMIZATION凸优化课程的代写代考和辅导服务!