MY-ASSIGNMENTEXPERT™可以为您提供catalog.usf.edu EEL6029 Statistical Inference统计推断的代写代考和辅导服务!
这是南佛罗里达州大学统计推断课程的代写成功案例。
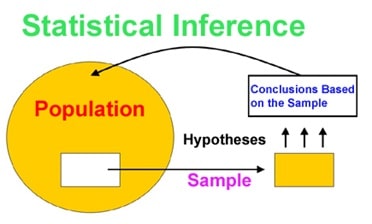
EEL6029 课程简介
Credit Hours: 3
This first-tier graduate course aims at establishing the background in mathematical statistics, and abstract modeling of complex cyber systems, data analytics, and Bayesian intelligence for graduate students in electrical and systems engineering.
Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability.Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
Prerequisites
Statistical inference makes propositions about a population, using data drawn from the population with some form of sampling. Given a hypothesis about a population, for which we wish to draw inferences, statistical inference consists of (first) selecting a statistical model of the process that generates the data and (second) deducing propositions from the model.
Konishi & Kitagawa state, “The majority of the problems in statistical inference can be considered to be problems related to statistical modeling”. Relatedly, Sir David Cox has said, “How the translation from subject-matter problem to statistical model is done is often the most critical part of an analysis”
EEL6029 Statistical Inference HELP(EXAM HELP, ONLINE TUTOR)
For each of the following experiments, describe a reasonable sample space:
(a) Toss a coin four times.
(b) Count the number of insect-damaged leaves on a plant.
(c) Measure the lifetime (in hours) of a particular brand of light bulb.
(d) Three people arrive at an airport checkpoint. Two of the three are randomly chosen to complete a survey.
(a) Toss coin 4 times:
$$
{(H, H, H, H), \ldots}=\left{\left(x_1, x_2, x_3, x_4\right): x_i \in{H, T}\right}
$$
or
$$
{0,1,2,3,4}
$$
(b) Count number of insect-damaged leaves:
$$
\begin{aligned}
{0,1, \ldots, N} & N=\text { # leaves (or upper bound) } \
{0,1,2, \ldots} & \text { if no upper bound is available }
\end{aligned}
$$
(c) Measure lifetime in hours:
$$
\begin{aligned}
{0,1,2, \ldots} & \text { if rounded (can put in upper limit) } \
{[0, \infty) } & \text { if fractional hours are allowed }
\end{aligned}
$$
(d) Two out of three people chosen to complete a survey: Suppose the people are labeled $A, B$, and $C$. One possible sample space is is the collection of all subsets of size 2 that can be chosen from the set ${A, B, C}$ :
$$
{{A, B},{A, C},{B, C}}
$$
Another possibility is the collection of all ordered pairs that can be formed:
$$
{(A, B),(B, A),(A, C),(C, A),(B, C),(C, B)} .
$$
The set-theoretic difference $A \backslash B=A \cap B^c$ is the set of all elements in $A$ that are not in $B$. The symmetric difference $A \Delta B=(A \backslash B) \cup(B \backslash A)$ is the set of all elements in either $A$ or $B$ but not both. Verify the following identities:
(a) $A \backslash B=A \backslash(A \cap B)$
(b) $A \Delta B=A^c \Delta B^c$
(c) $A \cup B=A \cup(B \backslash A)$
(d) $B=(B \cap A) \cup\left(B \cap A^c\right)$
(a) $A \backslash B$ is defined as $A \cap B^c$. To see that $A \backslash B=A \backslash(A \cap B)$ :
$$
\begin{array}{rlr}
A \backslash(A \cap B) & =A \cap(A \cap B)^c & \
& =A \cap\left(A^c \cup B^c\right) & \text { De Morgan’s law } \
& =\left(A \cap A^c\right) \cup\left(A \cap B^c\right) & \text { distributive law } \
& =\emptyset \cup\left(A \cap B^c\right) & \
& =A \backslash B
\end{array}
$$
De Morgan’s law distributive law
(b) $A \Delta B=A^c \Delta B^c$ : For any two sets $A$ and $B$
$$
\begin{array}{rlr}
A \backslash B & =A \cap B^c & \
& =B^c \cap A & \
& =B^c \cap\left(A^c\right)^c & \text { commutative law } \
& =B^c \backslash A^c &
\end{array}
$$
So
$$
\begin{aligned}
A \Delta B & =(A \backslash B) \cup(B \backslash A) \
& =\left(A^c \backslash B^c\right) \cup\left(B^c \backslash A^c\right) \
& =A^c \Delta B^c
\end{aligned}
$$
(c)
$$
\begin{aligned}
& A \cup B=A \cup(B \backslash A) \
& \begin{aligned}
A \cup B & =A \cup\left((B \cap A) \cup\left(B \cap A^c\right)\right) \
& =(A \cup(B \cap A)) \cup\left(B \cap A^c\right) \quad \text { by part (d) } \
& =A \cup\left(B \cap A^c\right)
\end{aligned} \quad \text { associative law }
\end{aligned}
$$
(d) $B=(B \cap A) \cup\left(B \cap A^c\right)$ :
$$
\begin{aligned}
(B \cap A) \cup\left(B \cap A^c\right) & =B \cap\left(A \cup A^c\right) \quad \text { distributive law } \
& =B \cap S \
& =B
\end{aligned}
$$

MY-ASSIGNMENTEXPERT™可以为您提供CATALOG.USF.EDU EEL6029 STATISTICAL INFERENCE统计推断的代写代考和辅导服务!




