MY-ASSIGNMENTEXPERT™可以为您提供helsink MAST31702 Probability Theory概率论课程的代写代考和辅导服务!
这是赫尔辛基大学概率论课程的代写成功案例。
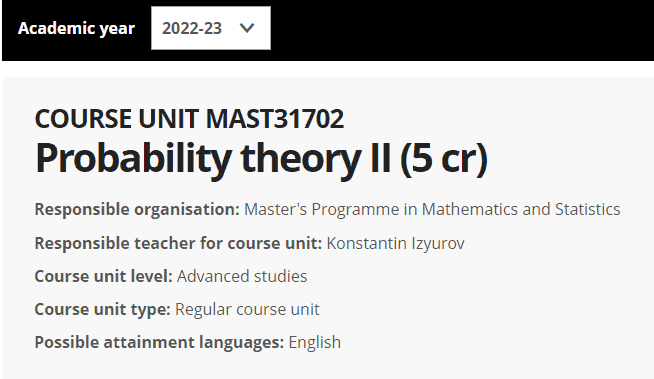
MAST31702课程简介
Responsible organisation: Master’s Programme in Mathematics and Statistics
Responsible teacher for course unit: Konstantin Izyurov
Course unit level: Advanced studies
Course unit type: Regular course unit
Possible attainment languages: English
For one course unit, usually one or several implementations (e.g. lecture courses, exams, seminars) are held during the academic year. Once the student has passed it, the student has attained the course unit and is given a grade. For some course units the implementations are held less frequently, for example only every other year.
Students at the Open University can enrol for implementations marked with this icon
Prerequisites
Prerequisites
Probability theory I and its prerequesites
Learning outcomes
The main point is to study the principal tools in modern Probability, namely, conditional expectations and martingales, together with some examples
Learning materials
Lecture notes; D. Williams: “Probability with martingales”, R. Durrett: “Probability: theory and examples”
Additional info
Target group
Optional course.
Master’s Programme in Mathematics and Statistics is responsible for the course.
The course belongs to the Mathematics and Applied mathematics module.
The course is available to students from other degree programmes.
Timing
Recommended time/stage of studies for completion: 1. year
Term/teaching period when the course will be offered: varying
Completion methods
Exam, other methods will be described later
MAST31702 Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
Consider the measurable space $[0, \infty)$ with the Borel sets. Consider the measurable function on this given by $X(\omega)=\omega^2$. Does there exist a probability measure on this measurable space for which the resulting law of $X$ has an exponential distribution with parameter 1 ? Find one or prove it does not exist. Is it unique?
If $X$ remains the same but $[0, \infty)$ were replaced by $(-\infty, \infty)$, would your answers change?
2(i). Give an example of a sequence $\left{X_n\right}$ of independent symmetric random variables such that
$$
\sum_n \operatorname{Var}\left(X_n\right)=\infty
$$
but
$$
\sum_n X_n \text { converges a.s. }
$$
Hint: Borel-Cantelli.
(ii). Give an example of a sequence $\left{X_n\right}$ of independent random variables with mean 0 such that
$$
\sum_n X_n=\infty \text { a.s. }
$$
Hint: Borel-Cantelli.
You are waiting for a bus at a bus stop. There are actually two buses that stop here. The one you want will arrive at a uniformly random time within the next 30 minutes. There is also a different bus, which will arrive at a uniformly random time within the next 60 minutes.
Given that exactly one of the buses arrives within the next 5 minutes, what is the probability that it is the one you want?
Note: we want a conditional probability here-and in the next two problems, as well.
Is it possible to have two distinct probability measures on a measurable space $(\Omega, \mathcal{F})$ and a subset $\mathcal{G} \subseteq \mathcal{F}$ such that $\mathcal{F}$ is the smallest $\sigma$-algebra containing $\mathcal{G}$ and the two probability measures agree on $\mathcal{G}$ ?
(i). Do there exist random variables $X_1, X_2, X_3$ which are not independent but which are pairwise independent?
(ii). If the events $E_1, E_2, E_3$ satisfy
$$
P\left(E_1 \cap E_2 \cap E_3\right)=P\left(E_1\right) P\left(E_2\right) P\left(E_3\right),
$$
are they necessarily independent?

MY-ASSIGNMENTEXPERT™可以为您提供HELSINK MATH280A PROBABILITY THEORY概率论课程的代写代考和辅导服务!