MY-ASSIGNMENTEXPERT™可以为您提供helsink MAST31702 Probability Theory概率论课程的代写代考和辅导服务!
这是赫尔辛基大学概率论课程的代写成功案例。

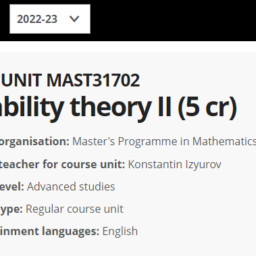
MAST31702课程简介
Responsible organisation: Master’s Programme in Mathematics and Statistics
Responsible teacher for course unit: Konstantin Izyurov
Course unit level: Advanced studies
Course unit type: Regular course unit
Possible attainment languages: English
For one course unit, usually one or several implementations (e.g. lecture courses, exams, seminars) are held during the academic year. Once the student has passed it, the student has attained the course unit and is given a grade. For some course units the implementations are held less frequently, for example only every other year.
Students at the Open University can enrol for implementations marked with this icon
Prerequisites
Prerequisites
Probability theory I and its prerequesites
Learning outcomes
The main point is to study the principal tools in modern Probability, namely, conditional expectations and martingales, together with some examples
Learning materials
Lecture notes; D. Williams: “Probability with martingales”, R. Durrett: “Probability: theory and examples”
Additional info
Target group
Optional course.
Master’s Programme in Mathematics and Statistics is responsible for the course.
The course belongs to the Mathematics and Applied mathematics module.
The course is available to students from other degree programmes.
Timing
Recommended time/stage of studies for completion: 1. year
Term/teaching period when the course will be offered: varying
Completion methods
Exam, other methods will be described later
MAST31702 Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
Data is collected on the weather in Marietta. Each month’s weather is summarized as ” $x$ sunny days, $y$ cloudy days, $z$ rainy days”. (Each day is exactly one of sunny, cloudy, or rainy.)
(a) Find the number of possible summaries of the weather in a 30-day month like September.
(b) If you wanted to know the probability that there are 10 sunny days, 10 cloudy days, and 10 rainy days in September, it would not be correct to take $\frac{1}{n}$, where $n$ is the answer to part (a). That’s because we are not sampling uniformly.
Assume that each kind of weather occurs with probability $\frac{1}{3}$, and that weather on different days is independent. Under this assumption, what is the probability that September’s weather is summarized as “10 sunny days, 10 cloudy days, 10 rainy days?”
A fair coin is flipped 5 times. Given that it lands heads 3 times out of 5 , what is the probability that the first of the five results was heads?
(a) Without doing fancy calculations, make a reasonable guess at the answer.
(It is not $\frac{1}{2}$. If you’re unsure, feel free to confirm your guess with me at any point before the homework is due.)
(b) Let $A$ be the event “the first flip was heads” and let $B$ be the event ” 3 out of the 5 flips were heads”.
Use binomial probability to compute $\operatorname{Pr}[A \cap B]$ and $\operatorname{Pr}[B]$. Then, compute $\operatorname{Pr}[A \mid B]$ using the definition of conditional probability, hopefully confirming your answer to part (a).
One of our definitions of weak convergence is that $\mu_n$ goes to $\mu_{\infty}$ if for all continuous $f$ vanishing at $\infty$
$$
\lim {n \rightarrow \infty} \int f d \mu_n=\int f d \mu{\infty}
$$
Note there is no uniformity over $f$. Consider the stronger property that
$$
\lim {n \rightarrow \infty} \sup {f \in A}\left|\int f d \mu_n-\int f d \mu_{\infty}\right|=0
$$
where $A$ is the set of continuous functions vanishing at $\infty$ which are bounded in absolute value by 1 . Give examples of convergence in distribution where this stronger property fails and also give (nontrivial) examples where this stronger property holds.
In elementary probability books, it is often stated, concerning the Central Limit Theorem, that it is a good approximation if $n \geq 30$. The only precise mathematical interpretation of this that I see is the following statement.
For every fixed interval $I$,
$$
\lim {n \rightarrow \infty} \sup {X_1 \in D}\left|\operatorname{Prob}\left(\frac{S_n}{\sqrt{n}} \in I\right)-\operatorname{Prob}(Z \in I)\right|=0
$$
where $D$ is the set of random variables with mean 0 and variance 1 and $Z$ is a standard normal. This corresponds to having the CLT hold uniformly over the distributions used for the summands.
a. Show that such a statement is false.
b. If $D(\epsilon, C)$ is the set of random variables with mean 0 and variance 1 and with
$$
E\left(\left|X_1\right|^{2+\epsilon}\right) \leq C
$$
show, using the Lindeberg-Feller Theorem that the above statement is true if $D$ is replaced by $D(\epsilon, C)$. This would say that the CLT holds uniformly over distributions used for the summands if we restrict to having a uniformly bounded $2+\epsilon$ moment.
(a). Let $X_1, X_2$ be two independent exponential random variables with parameter 1. Show that the pdf of $X_1-X_2$ is continuous without computing it.
(b). Use what you did in Part (a) to obtain the characteristic function of the Cauchy distribution.
MY-ASSIGNMENTEXPERT™可以为您提供HELSINK MATH280A PROBABILITY THEORY概率论课程的代写代考和辅导服务!