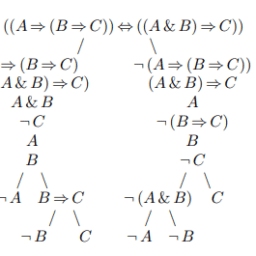MY-ASSIGNMENTEXPERT™可以为您提供 hawaii MATH455 Mathematical Logic数理逻辑的代写代考和辅导服务!
这是夏威夷大学 数理逻辑的代写成功案例。
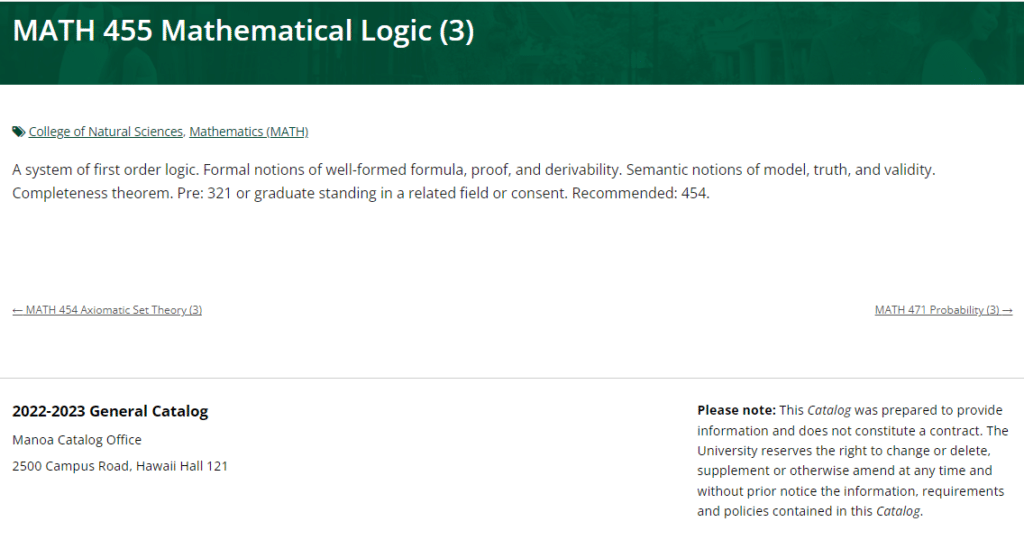
MATH455课程简介
A system of first order logic. Formal notions of well-formed formula, proof, and derivability. Semantic notions of model, truth, and validity. Completeness theorem. Pre: 321 or graduate standing in a related field or consent. Recommended: 454.Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics.
Prerequisites
Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and analysis. In the early 20th century it was shaped by David Hilbert’s program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to the program, and clarified the issues involved in proving consistency. Work in set theory showed that almost all ordinary mathematics can be formalized in terms of sets, although there are some theorems that cannot be proven in common axiom systems for set theory. Contemporary work in the foundations of mathematics often focuses on establishing which parts of mathematics can be formalized in particular formal systems (as in reverse mathematics) rather than trying to find theories in which all of mathematics can be developed.
MATH455 Mathematical Logic HELP(EXAM HELP, ONLINE TUTOR)
Formulate the following argument as a propositional formula.
If it has snowed, it will be poor driving. If it is poor driving, I will be late unless I start early. Indeed, it has snowed. Therefore, I must start early to avoid being late.
Solution. Use the following atoms.
$$
\begin{aligned}
& s: \text { it has snowed } \
& p: \text { it is poor driving } \
& l: \text { I will be late } \
& e: \text { I start early }
\end{aligned}
$$
The argument can be translated as follows: $s \Rightarrow p, p \Rightarrow(l \vee e), s$, therefore $(\neg l) \Rightarrow e$. Written as a single propositional formula, this becomes:
$$
(*) \quad((s \Rightarrow p) \&(p \Rightarrow(l \vee e)) \& s) \Rightarrow((\neg l) \Rightarrow e)
$$
Use the tableau method to demonstrate that this formula is logically valid.
Solution. The following closed tableau shows that $(*)$ is logically valid.
$$
\begin{gathered}
\mathrm{F}((s \Rightarrow p) \&(p \Rightarrow(l \vee e)) \& s) \Rightarrow((\neg l) \Rightarrow e) \
\mathrm{T}(s \Rightarrow p) \&(p \Rightarrow(l \vee e)) \& s \
\mathrm{~F}(\neg l) \Rightarrow e \
\mathrm{~T} s \Rightarrow p \
\mathrm{~T}(p \Rightarrow(l \vee e)) \& s \
\mathrm{~T} p \Rightarrow(l \vee e) \
\mathrm{T} s \
\mathrm{~T} \neg l \
\mathrm{~F} e \
\mathrm{~F} l \
/ \quad \backslash \
\mathrm{F} s \mathrm{~T} p \
\mathrm{~F} p \mathrm{~T} l \vee e \
/ \mathrm{T} l \
\mathrm{~T} e
\end{gathered}
$$
Brown, Jones, and Smith are suspected of a crime. They testify as follows:
Brown: Jones is guilty and Smith is innocent.
Jones: If Brown is guilty then so is Smith.
Smith: I’m innocent, but at least one of the others is guilty.
Let $b, j$, and $s$ be the statements “Brown is innocent,” “Jones is innocent,” “Smith is innocent”. Express the testimony of each suspect as a propositional formula. Write a truth table for the three testimonies.
Solution. The testimonies are:
$$
\begin{array}{ll}
B: & (\neg j) \& s \
J: & (\neg b) \Rightarrow(\neg s) \
S: & s \&((\neg b) \vee(\neg j))
\end{array}
$$
The truth table is:
$$
\begin{array}{lllllll}
& b & j & s & B & J & S \
1 & \mathrm{~T} & \mathrm{~T} & \mathrm{~T} & \mathrm{~F} & \mathrm{~T} & \mathrm{~F} \
2 & \mathrm{~T} & \mathrm{~T} & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} & \mathrm{~F} \
3 & \mathrm{~T} & \mathrm{~F} & \mathrm{~T} & \mathrm{~T} & \mathrm{~T} & \mathrm{~T} \
4 & \mathrm{~T} & \mathrm{~F} & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} & \mathrm{~F} \
5 & \mathrm{~F} & \mathrm{~T} & \mathrm{~T} & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} \
6 & \mathrm{~F} & \mathrm{~T} & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} & \mathrm{~F} \
7 & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} & \mathrm{~T} & \mathrm{~F} & \mathrm{~T} \
8 & \mathrm{~F} & \mathrm{~F} & \mathrm{~F} & \mathrm{~F} & \mathrm{~T} & \mathrm{~F}
\end{array}
$$
Use the above truth table to answer the following questions:
(a) Are the three testimonies consistent?
(b) The testimony of one of the suspects follows from that of another. Which from which?
(c) Assuming everybody is innocent, who committed perjury?
(d) Assuming all testimony is true, who is innocent and who is guilty? Solution. If all the testimony is true, we are in line 3 of the table. Thus Brown and Smith are innocent, while Jones is guilty.
(e) Assuming that the innocent told the truth and the guilty told lies, who is innocent and who is guilty
Solution. Yes, by line 3 of the table.
Solution. The table shows that $S$ is a logical consequence of $B$. In other words, Smith’s testimony follows from Brown’s.
Solution. If everybody is innocent, we are in line 1 of the table. Hence $B$ and $S$ are false, i.e., Brown and Smith lied.
Solution. Our assumption is $v(b)=v(B), v(j)=v(J), v(s)=v(S)$. Hence we are in line 6 of the table. Thus Jones is innocent, and Brown and Smith are guilty.

MY-ASSIGNMENTEXPERT™可以为您提供 HAWAII MATH455 MATHEMATICAL LOGIC数理逻辑的代写代考和辅导服务!