MY-ASSIGNMENTEXPERT™可以为您提供 handbook MTH3330 Operations research运筹学的代写代考和辅导服务!
这是莫纳什大学 运筹学的代写成功案例。
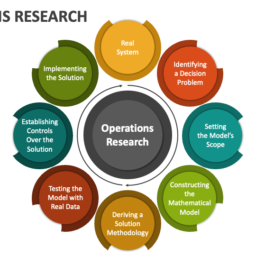
MATH3330课程简介
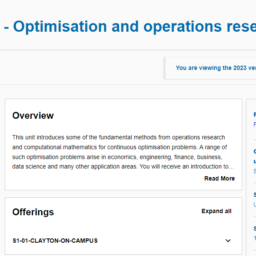
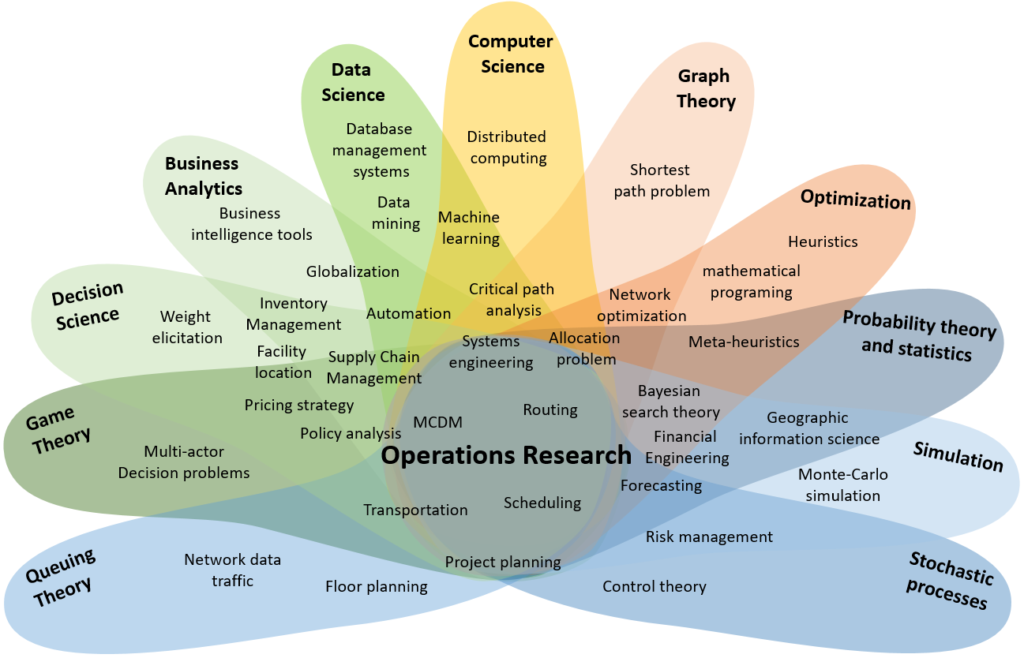
This unit introduces some of the fundamental methods from operations research and computational mathematics for continuous optimisation problems. A range of such optimisation problems arise in economics, engineering, finance, business, data science and many other application areas. You will receive an introduction to the mathematical theory of continuous optimisation with a focus on linear programming methods and smooth non-linear programming. This will broadly include duality theory, the simplex method for linear programming, network optimisation and iterative methods for unconstrained nonlinear optimisation. You will also learn to implement the computational methods efficiently, how to test their implementations for accuracy and performance, and to interpret the results. You will work on optimisation models for applications in a variety of fields. Applications may include examples of supply chain optimisation, economic modelling (including shadow prices), product mix optimisation, portfolio optimisation, parameter estimation and machine learning.
Prerequisites
Enrolment Rule
keyboard_arrow_down
PREREQUISITE: You must have passed one of MTH2051 or MTH3051 or if you are enrolled in the Bachelor of Applied Data Science MTH2019 or both of (MTH2010 or MTH2015) and (MTH2021 or MTH2025) or if you are enrolled in the Honours of Econometrics, ETC2440 (this requires manual enrolment).
Alternatively you must be enrolled in the Master of Financial Mathematics, the Master of Mathematics, or receive special permission from the unit coordinator.
MTH3330 Operations research HELP(EXAM HELP, ONLINE TUTOR)
Note that
$$
\begin{aligned}
E[1 / r(X)] & =\int(1 / r(x)) f(x) d x \
& =\int \frac{1-F(x)}{f(x)} f(x) d x \
& =\int 1-F(x) d x \
& =E[X]
\end{aligned}
$$
The last step is a very useful relation, as indicated in the hint; see page 580 of Ross.
The probability that machine 1 fails before time $t$ is $1-e^{-\lambda_1 t}$. The probability that machine 1 is still working at time $t$ is $e^{-\lambda_1 t}$. Conditional on machine 1 working at time $t$, the probability that machine 1 fails first is $\lambda_1 /\left(\lambda_1+\lambda_2\right)$. Hence the final answer is
$$
1-e^{-\lambda_1 t}+e^{-\lambda_1 t} \frac{\lambda_1}{\left(\lambda_1+\lambda_2\right)} .
$$
Use two facts: (1) the lack of memory property and (2) the fact that the minimum of independent exponential random variables is again exponential with a rate equal to the sum of the individual rates (rate equals reciprocal of the mean). Hence,
$$
P\left(A_1\right)=P\left(X>\min \left{Y_1, \ldots, Y_n\right}\right)=\frac{n \mu}{\lambda+n \mu} .
$$
Moreover,
$$
P\left(A_j \mid A_1 A_2 \ldots A_{j-1}\right)=\frac{(n-j+1) \mu}{\lambda+(n-j+1) \mu}
$$
Hence,
$$
\begin{aligned}
p & \equiv P\left(X>\max \left{Y_i\right}\right) \
& =P\left(A_1\right) P\left(A_2 \mid A_1\right) \ldots P\left(A_n \mid A_1 A_2 \ldots A_{n-1}\right) \
& =\prod_{j=1}^{j=n} \frac{(n-j+1) \mu}{\lambda+(n-j+1) \mu} .
\end{aligned}
$$
When $n=2$,
$$
\begin{aligned}
p & \equiv P\left(X>\max \left{Y_i\right}\right) \
& =\int_0^{\infty} P\left(\max \left{Y_i\right}<X \mid X=x\right) \lambda e^{-\lambda x} d x \
& =\int_0^{\infty} P\left(\max \left{Y_i\right}<x\right) \lambda e^{-\lambda x} d x \
& =\int_0^{\infty}\left(1-e^{-\mu x}\right)^2 \lambda e^{-\lambda x} d x \
& =\int_0^{\infty}\left(1-2 e^{-\mu x}+e^{-2 \mu x}\right) \lambda e^{-\lambda x} d x \
& =1-\frac{2 \lambda}{\lambda+\mu}+\frac{\lambda}{\lambda+2 \mu} \
& =\frac{2 \mu^2}{(\lambda+\mu)(\lambda+2 \mu)}
\end{aligned}
$$
This is an exercise in properties 2, 4 and 5 on the Concise Summary: (2) The minimum of independent exponential random variables is again exponential with a rate equal to the sum of the rates of the random variables considered in the minimum; (4) the probability that one exponential random variable is the minimum of several independent exponential random variables is its rate divided by the sum of the rates; (5) even more, the two events considered in (2) and (4) are actually independent! However, it is necessary to assume that all these exponential random variables are mutually independent. We make that assumption.
(a) This is property 4 above. This is just the probability one exponential variable is less than another:
$$
\frac{\mu_1}{\mu_1+\mu_3}
$$
(b) This is property 4 applied twice. You now have two independent events that must both happen, so it is the product of the probabilities:
$$
\frac{\mu_1}{\mu_1+\mu_3} \times \frac{\mu_2}{\mu_2+\mu_3}
$$
(c) Now you want to be very careful. You want to exploit all three properties. You will need the more complicated property (5). Let $T$ be the sojourn time of the new customer. To compute $E[T]$, we condition on the first event, i.e., whether the new customer finishes service at server 1 first $\left(S_1S_3\right)$. Let $T_0$ be the time up to the first event. Since $T_0=\min \left(S_1, S_3\right), E\left[T_0\right]=\frac{1}{\mu_1+\mu_3}$. Let $T^{\prime}=T-T_0$, the remaining sojourn time of the new customer. So,
$$
\begin{aligned}
E[T] & =E\left[T_0\right]+E\left[T^{\prime} \mid S_1>S_3\right] P\left(S_1>S_3\right)+E\left[T^{\prime} \mid S_1S_3$ is independent of $T_0$. Hence above we could just use $P\left(S_1>S_3\right)$ in the second term.
To obtain $E\left[T^{\prime} \mid S_1S_3\right)$. By the lack of memory property, the remaining service time of the old customer at server 3 is still $\exp \left(\mu_3\right)$. Let $T_0^{\prime}$ be the time up to this first event, i.e., $T_0^{\prime}=\min \left(S_2, S_3\right)$. Then $E\left[T_0^{\prime}\right]=\frac{1}{\mu_2+\mu_3}$. Let $T_r^{\prime}=T^{\prime}-T_0^{\prime}$, the remaining service sojourn time. So,
$$
\begin{aligned}
E\left[T^{\prime} \mid S_1S_3\right] P\left(S_2>S_3\right)+E\left[T_r^{\prime} \mid S_2<S_3\right] P\left(S_2<S_3\right) \
& =\left(\frac{1}{\mu_2+\mu_3}\right)+\left(\frac{1}{\mu_2}+\frac{1}{\mu_3}\right)\left(\frac{\mu_3}{\mu_2+\mu_3}\right)+\frac{2}{\mu_3}\left(\frac{\mu_2}{\mu_2+\mu_3}\right) .
\end{aligned}
$$
(d) Let $X_i$ be the service time at server $i$ for customer $X$ (new customer), $i=1,2,3$. Let $Y_j$ be the service time at server $j$ for customer $Y$ (old customer), $j=2,3$. We know that $X_i^{\prime} s$ and $Y_j^{\prime} s$ are independent and exponentially distributed (but with different means). Let $T$ be the total time required. Let $T_1=$ time until next event happens, and let $T^{\prime}=T-T_1$.
Then $E T=E T_1+E T^{\prime}$. Clearly $T_1=\min \left(X_1, Y_2\right)$, so $E T_1=\frac{1}{\mu_1+\mu_2}$. We remark that the distribution of $T_1$ is independent of the event $\left{X_1Y_2\right] \cdot P\left(X_1>Y_2\right)+E\left[T^{\prime} \mid X_1Y_2\right] \cdot\left(\frac{\mu_2}{\mu_1+\mu_2}\right)+E\left[T^{\prime} \mid X_1Y_2\right]$ is already computed in part (c), the only unknown here is $E\left[T^{\prime} \mid X_1<\right.$ $\left.Y_2\right]$. Note that $$ E\left[T^{\prime} \mid X_1Y_3\right] \cdot P\left(X_2>Y_3\right)+E\left[T^{\prime \prime} \mid X_2<Y_3\right] \cdot P\left(X_2<Y_3\right) \
& =\left(\frac{1}{\mu_2}+\frac{1}{\mu_3}\right) \cdot\left(\frac{\mu_3}{\mu_2+\mu_3}\right)+\frac{2}{\mu_3} \cdot\left(\frac{\mu_2}{\mu_2+\mu_3}\right)
\end{aligned}
$$
It’s not necessary to simplify this result.

MY-ASSIGNMENTEXPERT™可以为您提供 HANDBOOK MATH3202 OPERATIONS RESEARCH运筹学的代写代考和辅导服务!