MY-ASSIGNMENTEXPERT™可以为您提供helsink MAST31702 Probability Theory概率论课程的代写代考和辅导服务!
这是赫尔辛基大学概率论课程的代写成功案例。

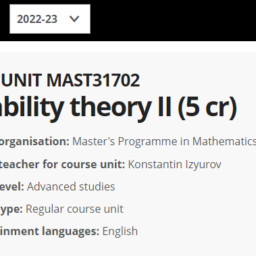
MAST31702课程简介
Responsible organisation: Master’s Programme in Mathematics and Statistics
Responsible teacher for course unit: Konstantin Izyurov
Course unit level: Advanced studies
Course unit type: Regular course unit
Possible attainment languages: English
For one course unit, usually one or several implementations (e.g. lecture courses, exams, seminars) are held during the academic year. Once the student has passed it, the student has attained the course unit and is given a grade. For some course units the implementations are held less frequently, for example only every other year.
Students at the Open University can enrol for implementations marked with this icon
Prerequisites
Prerequisites
Probability theory I and its prerequesites
Learning outcomes
The main point is to study the principal tools in modern Probability, namely, conditional expectations and martingales, together with some examples
Learning materials
Lecture notes; D. Williams: “Probability with martingales”, R. Durrett: “Probability: theory and examples”
Additional info
Target group
Optional course.
Master’s Programme in Mathematics and Statistics is responsible for the course.
The course belongs to the Mathematics and Applied mathematics module.
The course is available to students from other degree programmes.
Timing
Recommended time/stage of studies for completion: 1. year
Term/teaching period when the course will be offered: varying
Completion methods
Exam, other methods will be described later
MAST31702 Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
We have seen an example where convergence in probability does not imply convergence a.s. The following gives a very different construction.
Let $A_1, A_2, \ldots$ be independent events with $P\left(A_i\right)=p_i$. Determine necessary and sufficient conditions in terms of the $p_i$ ‘s such that the sequence $I_{A_i}$ converges to 0 in probability but not a.s.
Hint: Borel-Cantelli.
(Optional). We know that if $X_n$ are random variables, then $\sup _n X_n$ is a random variable. If we have random variables $X_t$, for $t \in[0,1]$, is $\sup _t X_t$ necessarily a random variable? Prove or give a counterexample.
Fix $\gamma>0$. Let $X_1, X_2, X_3, \ldots$ be independent random variables such that for each $i$
$$
P\left(X_i=i^\gamma\right)=P\left(X_i=-i^\gamma\right)=1 / 2 .
$$
a. Show that for $\gamma<1 / 2$,
$$
\left(\sum_{i=1}^n X_i\right) / n
$$
converges to 0 in probability.
b. Show that for $\gamma \geq 1$,
$$
\left(\sum_{i=1}^n X_i\right) / n
$$
does not converge to 0 in probability.
c. (Optional Challenge Problem)
Show that for $\gamma \in[1 / 2,1)$,
$$
\left(\sum_{i=1}^n X_i\right) / n
$$
does not converge to 0 in probability.
One way to do this, which I don’t want you to do since we haven’t gotten to these things yet, is using the Lindeberg-Feller Theorem which is a generalization of the central limit theorem. So, the point is to get an elementary argument from first principles. I haven’t thought about it myself and so I don’t know how elementary one can make it.
In the proof of the weak law of large numbers that we did in class, discuss whether pairwise independence (as opposed to full independence) suffices for the proof.
In class, we have proved that if $S_n$ is the sum of your winnings after $n$ plays of the St. Petersburg game, then
$$
S_n /(n \log n)
$$
approaches 1 in probability.
(a). Show that nonetheless
$$
\limsup _n S_n /(n \log n)=\infty \text { a.s. }
$$
Explain in words how it is possible that these two things can both hold.
(b). Show that
$$
\liminf _n S_n /(n \log n) \leq 1 \text { a.s. }
$$
It is in fact the case that
$$
\liminf _n S_n /(n \log n)=1 \text { a.s. }
$$
but you do not need to prove that.

MY-ASSIGNMENTEXPERT™可以为您提供HELSINK MATH280A PROBABILITY THEORY概率论课程的代写代考和辅导服务!