如果你也在 怎样代写广义相对论General Relativity 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。广义相对论General Relativity又称广义相对论和爱因斯坦引力理论,是爱因斯坦在1915年发表的引力几何理论,是目前现代物理学中对引力的描述。广义相对论概括了狭义相对论并完善了牛顿的万有引力定律,将引力统一描述为空间和时间或四维时空的几何属性。特别是,时空的曲率与任何物质和辐射的能量和动量直接相关。这种关系是由爱因斯坦场方程规定的,这是一个二阶偏微分方程系统。
广义相对论General Relativity描述经典引力的牛顿万有引力定律,可以看作是广义相对论对静止质量分布周围几乎平坦的时空几何的预测。然而,广义相对论的一些预言却超出了经典物理学中牛顿的万有引力定律。这些预言涉及时间的流逝、空间的几何、自由落体的运动和光的传播,包括引力时间膨胀、引力透镜、光的引力红移、夏皮罗时间延迟和奇点/黑洞。到目前为止,对广义相对论的所有测试都被证明与该理论一致。广义相对论的时间相关解使我们能够谈论宇宙的历史,并为宇宙学提供了现代框架,从而导致了大爆炸和宇宙微波背景辐射的发现。尽管引入了一些替代理论,广义相对论仍然是与实验数据一致的最简单的理论。然而,广义相对论与量子物理学定律的协调仍然是一个问题,因为缺乏一个自洽的量子引力理论;以及引力如何与三种非引力–强、弱和电磁力统一起来。
广义相对论General Relativity代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的广义相对论General Relativity作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此广义相对论General Relativity作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在广义相对论General Relativity代写方面经验极为丰富,各种广义相对论General Relativity相关的作业也就用不着说。
物理代写|广义相对论代写General Relativity代考|Gravitational Red Shift
Now that $g_{00}$ has been obtained in the context of GR, the question of how gravity affects clocks can be reconsidered. Here, it is done in a completely GR context. A review of the material in Section 2.8 will prove worthwhile. The present discussion works, not only for the weak gravity metric under consideration, but for future exact metrics.
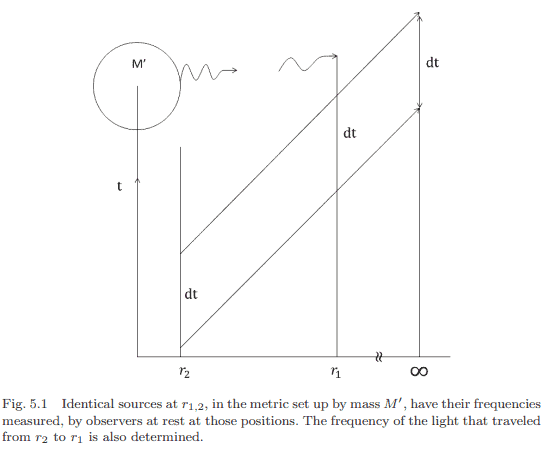
So suppose, as in Fig. 5.1, a helium source at $r_2$ emits photons. The photons are observed by experimenters at rest at $r_1$ and $r_2$, having traveled in the metric set up by source mass $M^{\prime}$. The observer at $r_1$ in weaker gravity also has a helium source. The desired prediction, that can be compared with measurement, is the ratio $\nu_{2,1} / \nu_{2,2}=\nu_{2,1} / \nu_{1,1}$. Here, the numerator is the frequency of the light from $r_2$ measured at $r_1$, and the denominator is the frequency from identical sources measured at the positions of the sources. The first method of predicting this ratio makes use of invariants,
$$
\begin{aligned}
{\left[P^\mu\right]{\text {photon }}\left[U\mu\right]{\text {obs. }} } & =\left[P^\mu\right]{\text {photon }}\left[g_{\mu \nu} \frac{d x^\nu}{d \tau}\right]{\text {obs. }} \ & =\left[P^0\right]{\text {photon }}\left[g_{00} \frac{d t}{d \tau}\right]{\text {obs. }}=\left[P^0\right]{\text {photon }}\left(\left[-g_{00}\right]{\text {obs. }}\right)^{1 / 2} \ & =h \nu{2,2}\left(-g_{00}(2)\right)^{1 / 2}=h \nu_{2,1}\left(-g_{00}(1)\right)^{1 / 2} \
& =h \nu_{2,2}\left(1-2 M^{\prime} / r_2\right)^{1 / 2}=h \nu_{2,1}\left(1-2 M^{\prime} / r_1\right)^{1 / 2} \
\nu_{2,1} / \nu_{1,1} & =\nu_{2,1} / \nu_{2,2}=\left(1-2 M^{\prime} / r_2\right)^{1 / 2}\left(1-2 M^{\prime} / r_1\right)^{-1 / 2} \
& \approx 1-M^{\prime}\left(1 / r_2-1 / r_1\right)
\end{aligned}
$$
A second way to get this result is to note, from Fig. 5.1, the world lines of successive wave crests. They travel from $r_2$ to $r_1$ and to a faraway point, along identical geodesics with speed $c$. The journey times are the same. The faraway at-rest observer is not experiencing gravity. That observer measures the proper-time period between crests $d \tau_{\infty}=d t$. This is the coordinate time period. Working backwards to $r_{1,2}$, along the world lines of the crests, one can see that $d t$ is unchanged. However, the proper-time periods are the inverses of the frequencies,
$$
\begin{aligned}
\frac{d \tau_{2,2}}{d \tau_{2,1}} & =\frac{d t_{2,2}}{d t_{2,1}}\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2}=\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2}, \
\frac{\nu_{2,1}}{\nu_{2,2}} & =\frac{\nu_{2,1}}{\nu_{1,1}}=\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2} \approx 1-M^{\prime}\left(1 / r_2-1 / r_1\right),
\end{aligned}
$$
exactly as in Eq. (5.7).
Since $r_1>r_2$, gravity is weaker at $r_1$. Then $\nu_{2,1} / \nu_{1,1}<1$ and $\lambda_{2,1} / \lambda_{1,1}>1$. This is known as the gravitational red shift. It is the same result obtained in Section 2.8 using energy conservation and relativistic mass. That worked for weak gravity. In addition, $d \tau_{2,2} / d \tau_{2,1}<1$.
物理代写|广义相对论代写General Relativity代考|Einstein’s Field Equations
In Newton’s theory, the gravitational potential $\Psi_G$ is related to the source mass density $\rho_M$. This was seen in Eq. (5.1). For a source point mass $M^{\prime}$, the solution is $\Psi_G=-M^{\prime} / r$, where $r$ is the distance from the mass. Einstein’s theory is based on curved spacetime, and one must determine the metric. The equation that relates the metric to the source must be covariant, a tensor equation. All observers would write the same equation, using their own coordinates. Instead of a mass density, that is related to the $T^{00}$ element of the energy-momentum tensor, a covariant theory requires the entire tensor to be the source. So the correct equation would look like,
$$
O\left(g^{\mu \nu}\right)=a T^{\mu \nu}
$$
where $a$ is a constant, and $O$ is a differential operator. The tensor properties of both sides of the above equation must be the same. Those are: each side is a symmetric tensor, and since momentum is conserved, each tensor has vanishing divergence $T^{\mu \nu} ; \nu=0$. The tensor $T^{\mu \nu}$ is discussed in detail later, when it is needed. In the solar system, planets move in vacuum, in the metric set up by the sun. Thus $T^{\mu \nu}=0$, and the constant $a$ doesn’t matter.
For curved spacetime, operator $O$ will at least contain terms with the metric tensor and its first and second partial derivatives. That’s just what is found in the Ricci tensor $R^{\mu \nu}$. A nonzero $R_{\nu \xi \chi}^\mu$ somewhere, means finite curvature, and the presence of gravity. Another way to say this is, at the position of the earth, it may be that $R^{\mu \nu}=0$. However, at least one of the elements of the curvature tensor $R_{\nu \xi \chi}^\mu \neq 0$. Einstein struggled with this problem for many years before finally finding the simplest form,
$$
O\left(g^{\mu \nu}\right)=R^{\mu \nu}+a^{\prime} g^{\mu \nu} R+\Lambda g^{\mu \nu}=a T^{\mu \nu}
$$
where $a^{\prime}$ and $\Lambda$ are constants.
广义相对论代写
物理代写|广义相对论代写General Relativity代考|Gravitational Red Shift
现在已经在GR的背景下获得了$g_{00}$,重力如何影响时钟的问题可以重新考虑。在这里,它是在完全GR的上下文中完成的。复习一下第2.8节中的材料是值得的。本文的讨论不仅适用于所考虑的弱引力度量,而且适用于未来的精确度量。
那么假设,如图5.1所示,$r_2$处的氦源发射光子。实验人员在$r_1$和$r_2$处观察到静止的光子,它们以源质量$M^{\prime}$建立的度规运动。在引力较弱的$r_1$观测者也有一个氦源。期望的预测,可以与测量相比较,是比率$\nu_{2,1} / \nu_{2,2}=\nu_{2,1} / \nu_{1,1}$。在这里,分子是在$r_1$测量的来自$r_2$的光的频率,分母是在光源位置测量的来自相同光源的频率。预测该比率的第一种方法是使用不变量,
$$
\begin{aligned}
{\left[P^\mu\right]{\text {photon }}\left[U\mu\right]{\text {obs. }} } & =\left[P^\mu\right]{\text {photon }}\left[g_{\mu \nu} \frac{d x^\nu}{d \tau}\right]{\text {obs. }} \ & =\left[P^0\right]{\text {photon }}\left[g_{00} \frac{d t}{d \tau}\right]{\text {obs. }}=\left[P^0\right]{\text {photon }}\left(\left[-g_{00}\right]{\text {obs. }}\right)^{1 / 2} \ & =h \nu{2,2}\left(-g_{00}(2)\right)^{1 / 2}=h \nu_{2,1}\left(-g_{00}(1)\right)^{1 / 2} \
& =h \nu_{2,2}\left(1-2 M^{\prime} / r_2\right)^{1 / 2}=h \nu_{2,1}\left(1-2 M^{\prime} / r_1\right)^{1 / 2} \
\nu_{2,1} / \nu_{1,1} & =\nu_{2,1} / \nu_{2,2}=\left(1-2 M^{\prime} / r_2\right)^{1 / 2}\left(1-2 M^{\prime} / r_1\right)^{-1 / 2} \
& \approx 1-M^{\prime}\left(1 / r_2-1 / r_1\right)
\end{aligned}
$$
第二种方法是从图5.1中注意到连续波峰的世界线。它们以$c$的速度沿着相同的测地线从$r_2$到达$r_1$并到达一个遥远的点。旅程时间是一样的。远处静止的观察者没有感受到重力。该观察者测量波峰之间的适当时间周期$d \tau_{\infty}=d t$。这是坐标时间。沿着波峰的世界线往回看$r_{1,2}$,可以看到$d t$没有变化。然而,固有周期是频率的倒数,
$$
\begin{aligned}
\frac{d \tau_{2,2}}{d \tau_{2,1}} & =\frac{d t_{2,2}}{d t_{2,1}}\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2}=\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2}, \
\frac{\nu_{2,1}}{\nu_{2,2}} & =\frac{\nu_{2,1}}{\nu_{1,1}}=\left(\frac{-g_{00}(2)}{-g_{00}(1)}\right)^{1 / 2} \approx 1-M^{\prime}\left(1 / r_2-1 / r_1\right),
\end{aligned}
$$
与Eq.(5.7)完全相同。
由于$r_1>r_2$,引力在$r_1$处较弱。然后是$\nu_{2,1} / \nu_{1,1}<1$和$\lambda_{2,1} / \lambda_{1,1}>1$。这被称为引力红移。这与第2.8节使用能量守恒和相对论质量得到的结果相同。这在弱重力下是可行的。此外,$d \tau_{2,2} / d \tau_{2,1}<1$ .
物理代写|广义相对论代写General Relativity代考|Einstein’s Field Equations
在牛顿的理论中,引力势$\Psi_G$与源质量密度$\rho_M$有关。这可以从Eq.(5.1)中看出。对于一个质点$M^{\prime}$,解是$\Psi_G=-M^{\prime} / r$,其中$r$是到质点的距离。爱因斯坦的理论是建立在弯曲时空的基础上的,人们必须确定度规。把度规和源联系起来的方程必须是协变的,一个张量方程。所有的观察者都会用自己的坐标写出相同的方程。协变理论要求整个张量作为源,而不是质量密度,它与能量动量张量的$T^{00}$元素有关。所以正确的方程应该是,
$$
O\left(g^{\mu \nu}\right)=a T^{\mu \nu}
$$
其中$a$是常数,$O$是微分算子。上述方程两边的张量性质必须相同。它们是:每条边都是对称张量,由于动量是守恒的,每个张量都有散度消失$T^{\mu \nu} ; \nu=0$。张量$T^{\mu \nu}$稍后将在需要时详细讨论。在太阳系中,行星在真空中运行,这是由太阳设定的公制。因此$T^{\mu \nu}=0$,常数$a$不重要。
对于弯曲时空,算符$O$至少包含度规张量及其一阶和二阶偏导数的项。这就是我们在里奇张量$R^{\mu \nu}$中发现的。某个地方的非零$R_{\nu \xi \chi}^\mu$,意味着曲率有限,重力存在。另一种说法是,在地球的位置,它可能是$R^{\mu \nu}=0$。然而,曲率张量的至少一个元素$R_{\nu \xi \chi}^\mu \neq 0$。爱因斯坦在这个问题上挣扎了很多年,最终找到了最简单的形式,
$$
O\left(g^{\mu \nu}\right)=R^{\mu \nu}+a^{\prime} g^{\mu \nu} R+\Lambda g^{\mu \nu}=a T^{\mu \nu}
$$
其中$a^{\prime}$和$\Lambda$是常量。

物理代写|广义相对论代写General Relativity代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。