统计代写|STAT3023 Statistical Inference

MY-ASSIGNMENTEXPERT™可以为您提供sydney STAT3023 Statistical Inference统计推断的代写代考和辅导服务！

这是悉尼大学统计推断课程的代写成功案例。

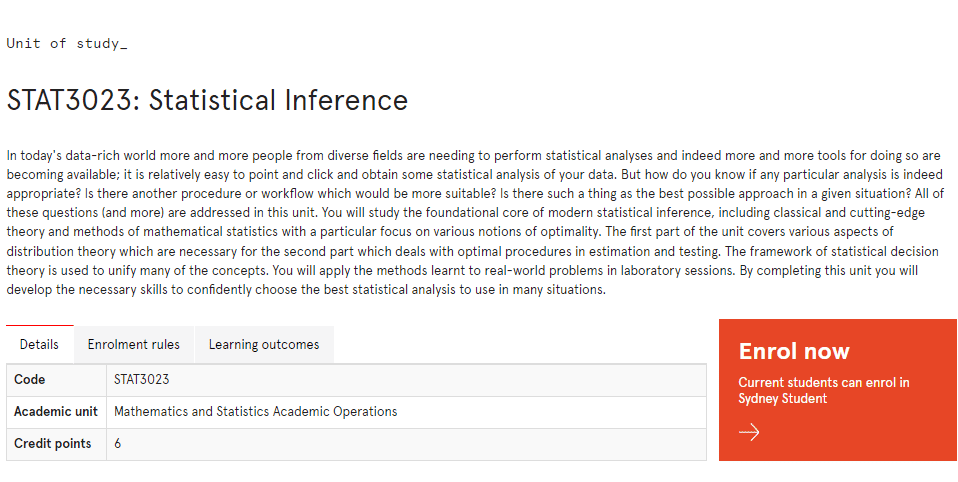
STAT3023 课程简介

In today’s data-rich world more and more people from diverse fields are needing to perform statistical analyses and indeed more and more tools for doing so are becoming available; it is relatively easy to point and click and obtain some statistical analysis of your data. But how do you know if any particular analysis is indeed appropriate? Is there another procedure or workflow which would be more suitable? Is there such a thing as the best possible approach in a given situation? All of these questions (and more) are addressed in this unit. You will study the foundational core of modern statistical inference, including classical and cutting-edge theory and methods of mathematical statistics with a particular focus on various notions of optimality. The first part of the unit covers various aspects of distribution theory which are necessary for the second part which deals with optimal procedures in estimation and testing. The framework of statistical decision theory is used to unify many of the concepts. You will apply the methods learnt to real-world problems in laboratory sessions. By completing this unit you will develop the necessary skills to confidently choose the best statistical analysis to use in many situations.

Prerequisites 

At the completion of this unit, you should be able to:

• LO1. deduce the (limiting) distribution of sums of random variables using moment-generating functions
• LO2. derive the distribution of a transformation of two (or more) continuous random variables
• LO3. derive marginal and conditional distributions associated with certain multivariate distributions
• LO4. classify many common distributions as belonging to an exponential family
• LO5. derive and implement maximum likelihood methods in various estimation and testing problems
• LO6. formulate and solve various inferential problems in a decision theory framework
• LO7. derive and apply optimal procedures in various problems, including Bayes rules, minimax rules, minimum variance unbiased estimators and most powerful tests.

STAT3023 Statistical Inference HELP（EXAM HELP， ONLINE TUTOR）

(a) One possible approach:
$>\operatorname{sapply}(\operatorname{seq}(0.2,0.9$, by $=0.2)$, function(p) mean replicate 10000, $\operatorname{sim} 1(p))$
[1] 0.49130 .49650 .50340 .4991
This suggests that the probability of heads may be 0.5 for any $p$.
(b) Let $A$ be the event that the process returns a head, and let $B$ be the event that the process ends after the first two flips. Then
$$
P(A)=P(A \cap B)+P\left(A \mid B^c\right) P\left(B^c\right) .
$$
Now $A \cap B$ is the event that the first toss is a tail and the second toss is a head, so $P(A \cap B)=(1-p) p . B$ is the event that either the first toss is a head and the second a tail, or the first is a tail and the second is a head; so $P(B)=2 p(1-p)$ and $P\left(B^c\right)=1-2 p(1-p)$. If the process does not end with the first two tosses then it starts over again independently, so $P\left(A \mid B^c\right)=P(A)$. Therefore $P(A)$ satisfies
$$
P(A)=p(1-p)+P(A)(1-2 p(1-p))
$$
and thus
$$
P(A)=\frac{p(1-p)}{2 p(1-p)}=\frac{1}{2},
$$
as the simulation in part (a) suggests. The requirement that $p>0$ and $p<1$ ensures that the denominator is positive and that the process is guaranteed to end.

(a) The derivatives are
$$
\begin{aligned}
G^{\prime}(t) & =\sum_{n=1}^{\infty} n t^{n-1} p_n \
G^{\prime \prime}(t) & =\sum_{n=2}^{\infty} n(n-1) t^{n-2} p_n \
& \vdots \
G^{(k)}(t) & =\sum_{n=k}^{\infty} \frac{n !}{(n-k) !} t^{n-2} p_n .
\end{aligned}
$$
At $t=0$ all terms except the first are zero, so
$$
\begin{aligned}
& G(0)=p_0 \
& G^{\prime}(0)=p_1 \
& G^{\prime \prime}(0)=2 p_2 \
& \vdots \
& G^{(k)}(0)=k ! p_k .
\end{aligned}
$$
So $p_k=G^{(k)}(0) / k$ !. This is the reason $G$ is called the probability generating function.
(b) For the binomial distribution
$$
G(t)=\sum_{k=0}^n t^k\left(\begin{array}{l}
n \
k
\end{array}\right) p^k(1-p)^{n-k}=\sum_{k=0}^n\left(\begin{array}{l}
n \
k
\end{array}\right)(t p)^k(1-p)^{n-k}=(t p+1-p)^n
$$
by the binomial theorem.
(c) For the geometric distribution
$$
G(t)=\sum_{n=1}^{\infty} t^n p(1-p)^{n-1}=t p \sum_{n=1}^{\infty}[t(1-p)]^{n-1}=\frac{t p}{1-t(1-p)}
$$

For a non-negative random variable $X$ we can write
$$
X=\int_0^X 1 d t=\int_0^{\infty} 1_{{t<X}} d t
$$
and therefore
$$
E[X]=E\left[\int_0^{\infty} 1_{{t<X}} d t\right]
$$
Reversing the order of integration yields
$$
E[X]=\int_0^{\infty} E\left[1_{{t<X}}\right] d t=\int_0^{\infty} P(t<X) d t=\int_0^{\infty}(1-F(t)) d t
$$
The interchange of expectation and integration for integrating a non-negative function is justified by a result known as Tonelli’s theorem.

MY-ASSIGNMENTEXPERT™可以为您提供CATALOG.USF.EDU EEL6029 STATISTICAL INFERENCE统计推断的代写代考和辅导服务！