MY-ASSIGNMENTEXPERT™可以为您提供stanford.edu MS&E310 Linear Programming线性规划课程的代写代考和辅导服务!
这是斯坦福大学 线性规划课程的代写成功案例。

MS&E310课程简介
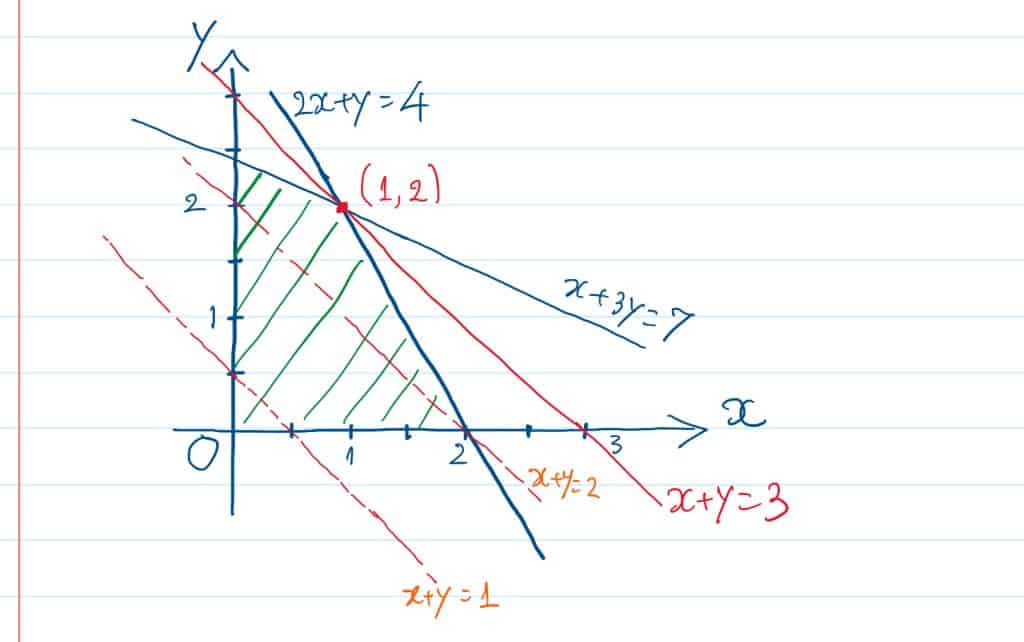
Topics include: Problem formulation of standard (conic) linear programming models, the theory of polyhedral and conic convex sets, linear inequalities, alternative theorems and duality, sensitivity analyses and economic interpretations, and relaxations of harder optimization problems. Algorithms include the simplex method, interior-point methods, and ADMM and other (first-order) iterative methods. Complexity and/or computation efficiency analysis for linear programming. Applications include dynamic resource allocation, on-line mechanism design, algorithmic game-theory, SVM/data-classification, and MDP/reinforced learning.
Prerequisites
The field of optimization is concerned with the study of maximization and minimization of mathematical functions. Very often the arguments of (i.e., variables in) these functions are subject to side conditions or constraints. By virtue of its great utility in such diverse areas as applied science, engineering, economics, finance, medicine, and statistics, optimization holds an important place in the practical world and the scientific world. Indeed, as far back as the Eighteenth Century, the famous Swiss mathematician and physicist Leonhard Euler (1707-1783) proclaimed that … nothing at all takes place in the Universe in which some rule of maximum or minimum does not appear. The subject is so pervasive that we even find some optimization terms in our everyday language.
MS&E310 Linear Programming HELP(EXAM HELP, ONLINE TUTOR)
Let $G=(V, E)$ be an undirected graph, and let $s$ and $t$ be two vertices of $G$. Give an efficient algorithm for computing the number of different shortest paths from $s$ to $t$. The length of a path is the number of edges on it, and two paths are different if the sets of edges that they use are different. You shouldn’t return the actual paths, just their number.
Hint 1: Store some information at each node.
Hint 2: If your solution has a “count +1 ” someplace in it, it’s probably wrong.
(a) You are given a network of biking trails for a park in the form of an undirected graph $G=(V, E)$. Give an $O(|V|)$-time algorithm to check whether the park contains a set of trails that form a loop (i.e. a cycle: a path that you could ride around forever without turning around). Note that the running time of your algorithm should not depend on $|E|$, the number of trails. You don’t need to output the cycle; just return YES or NO depending on whether it exists.
(b) Suppose, to avoid collisions between bikes, the trails each have an enforced direction: you are allowed to go only the posted direction on a trail. Either argue that, with minor changes, your algorithm for part (a) still works in $O(|V|)$ time to find a biking loop or explain why it does not.
Use DFS to argue that if every vertex of an undirected graph $G$ has at least $d \geq 2$ neighbors, then $G$ contains a cycle of length at least $d$.
Let $G=(V, E)$ be a connected, undirected graph, and suppose $T_s=(V, F)$ is a tree on $G$ created by exploring $G$ using depth-first search starting from vertex $s$. Vertex $s$ is the root of tree $T_s$. Argue that $s$ has more than one child in $T_s$ if and only if removing $s$ from $G$ breaks $G$ into several disconnected parts.
The diameter of a connected, undirected graph $G=(V, E)$ is the length (in number of edges) of the longest shortest path between two nodes. (a) Show that if the diameter of a graph is $d$ then there is some set $S \subseteq V$ with $|S| \leq n /(d-1)$ such that removing the vertices in $S$ from the graph would break it into several disconnected pieces. (b) Give an efficient algorithm to find $S$.
MY-ASSIGNMENTEXPERT™可以为您提供STANFORD.EDU MS&E310 LINEAR PROGRAMMING线性规划课程的代写代考和辅导服务!