MY-ASSIGNMENTEXPERT™可以为您提供 handbook MAST20026 Real Analysis实分析的代写代考和辅导服务!
这是墨尔本大学 实分析课程的代写成功案例。
MAST20026课程简介
This subject introduces the field of mathematical analysis both with a careful theoretical framework as well as selected applications. Many of the important results are proved rigorously and students are introduced to methods of proof such as mathematical induction and proof by contradiction.
The important distinction between the real numbers and the rational numbers is emphasized and used to motivate rigorous notions of convergence and divergence of sequences, including the Cauchy criterion. These ideas are extended to cover the theory of infinite series, including common tests for convergence and divergence. A similar treatment of continuity and differentiability of functions of a single variable leads to applications such as the Mean Value Theorem and Taylor’s theorem. The definitions and properties of the Riemann integral allow rigorous proof of the Fundamental Theorem of Calculus. The convergence properties of sequences and series are explored, with applications to power series representations of elementary functions and their generation by Taylor series. Fourier series are introduced as a way to represent periodic functions.
Prerequisites
On completion of this subject students should
- Acquire an appreciation of rigour in mathematics, be able to use proof by induction, proof by contradiction, and to use epsilon-delta proofs both as a theoretical tool and a tool of approximation;
- Understand the theory and applications of the Riemann integral and improper integrals;
- Be able to determine the convergence and divergence of infinite series;
- Have a good knowledge of the theory and practice of power series expansions and Taylor polynomial approximations; and
- Understand the role of Fourier series in representing periodic functions.
MAST20026 Real Analysis HELP(EXAM HELP, ONLINE TUTOR)
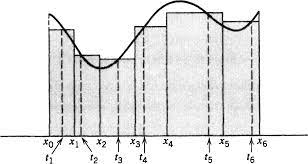
Show that there is a continuous, strictly increasing function on the interval $[0,1]$ that maps a set of positive measure onto a set of measure zero.
Let $f$ be an increasing function on the open interval $I$. For $x_0 \in I$ show that $\mathrm{f}$ is continuous at $x_0$ if and only if there are sequences $\left{a_n\right}$ and $\left{b_n\right}$ in $I$ such that for each $n, a_n<x_0<b_n$, and $\lim _{n \rightarrow \infty}\left(f\left(b_n\right)-f\left(a_n\right)\right)=0$.
Show that if $f$ is any increasing function on $[0,1]$ that agrees with the Cantor-Lebesgue function $\phi$ on the complement of the Cantor set, then $f=\phi$ on all of $(0,1)$.
Let $f$ be a continuous function defined on $E$. Is it true that $f^{-1}(A)$ is always measurable if $A$ is measurable?
Let the function $f:[a, b] \longrightarrow \mathbb{R}$ be Lipschitz, that is, there is a constant $c \geq 0$ such that for all $u, v \in[a, b]$, $|f(u)-f(v)| \leq c|u-v|$. Show that $f$ maps a set of measure zero onto a set of measure zero. Show that $f$ maps an $F_\sigma$ set onto an $F_\sigma$ set. Conclude that $\mathrm{f}$ maps a measurable set to a measurable set.
Let $F$ be the subset of $[0,1]$ constructed in the same manner as the Cantor set except that each of the intervals removed at the $n$th deletion stage has length $\alpha 3^{-n}$ with $0<\alpha<1$. Show that $F$ is a closed set, $[0,1] \backslash F$ dense in $[0,1]$, and $m(F)=1-\alpha$. Such a set $F$ is called a generalized Cantor set.

MY-ASSIGNMENTEXPERT™可以为您提供 HANDBOOK MAST20026 REAL ANALYSIS实分析的代写代考和辅导服务!