MY-ASSIGNMENTEXPERT™可以为您提供manoa.hawaii MATH414 Optimization Theory最优化的代写代考和辅导服务!
这是夏威夷大学最优化的代写成功案例。
MATH414课程简介
Introduction to theory and methods for optimization. Topics may include least square analysis, search methods, conjugate direction methods, linear programming, integer programming, and constrained optimization. Pre: 243 or 253A, and 307 or 311; or consent.
Mathematical optimization (alternatively spelled optimisation) or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives.[1] It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering[2] to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries
Prerequisites
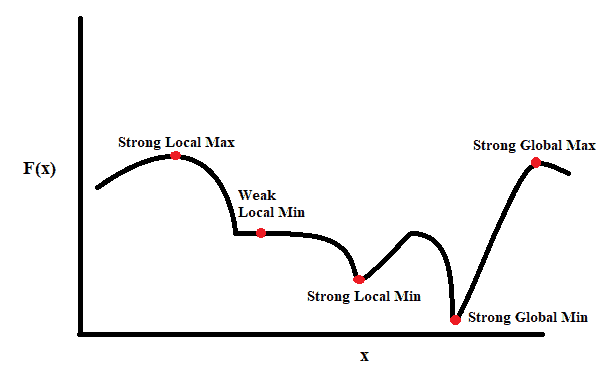
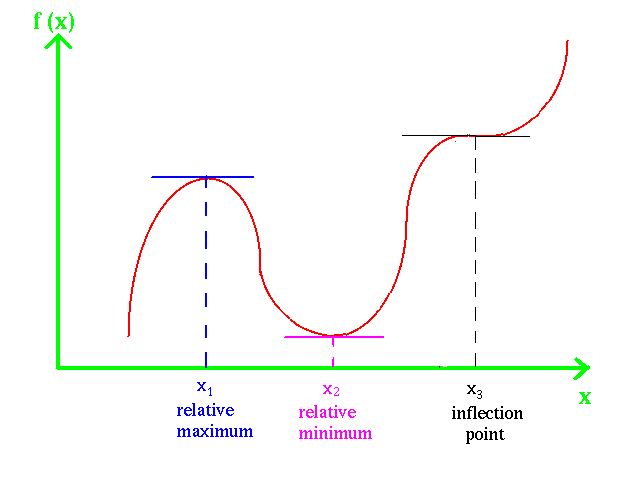
In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding “best available” values of some objective function given a defined domain (or input), including a variety of different types of objective functions and different types of domains.
MATH414 Optimization Theory HELP(EXAM HELP, ONLINE TUTOR)
Given $A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m, c \in \mathbb{R}^n$, the primal central path $\mathcal{C}_P$ is the trajectory of all points $x(\tau) \in \mathbb{R}^n, x(\tau)>0, \tau>0$, which solve the nonlinear system
$$
\text { (*) } \quad f_P(x, \lambda, \tau):=\left(\begin{array}{l}
A x-b \
\tau D_x^{-1} e+A^T \lambda-c
\end{array}\right)=\left(\begin{array}{l}
0 \
0
\end{array}\right)
$$
for some $\lambda=\lambda(\tau) \in \mathbb{R}^m$, where $D_x:=\operatorname{diag}\left(x_1, \ldots, x_n\right)$ and $e=(1, \ldots, 1)^T$. Consider the specific example
$$
A=\left(\begin{array}{cccc}
-1 & 1 & 1 & 0 \
1 & 1 & 0 & 1
\end{array}\right) \quad, \quad b=(2,4)^T \quad, \quad c=(1,2,0,0)^T
$$
(i) Specify the nonlinear system defining the associated primal central path.
(ii) Show that the elimination of $x_3, x_4$ and $\lambda_1, \lambda_2$ from the nonlinear system in (i) gives rise to a reduced parameter dependent nonlinear system in $x_1, x_2$,
$$
f\left(x_1, x_2, \tau\right)=0
$$
Compute this nonlinear system.
(iii) Show by the implicit function theorem that for every $\tau>0$ the nonlinear system from (ii) has a unique solution $\left(x_1(\tau), x_2(\tau)\right)$ in a vicinity of $(1,3)^T$.
(iv) If $x(\tau)=\left(x_1(\tau), x_2(\tau)\right)^T$ is the solution of the nonlinear system from (ii), show that
$$
\lim _{\tau \rightarrow 0} x(\tau)=(1,3)^T .
$$
What does this result tell you?
Karmarkar’s celebrated interior point algorithm focuses solely on the primal problem measuring progress towards optimality by means of a logarithmic potential function different from the one in the definition of the primal central path. Soon after Karmarkar, Renegar devised an algorithm that uses Newton’s method in conjunction with another logarithmic function, namely
$$
\begin{gathered}
\text { () } \quad \text { minimize }-n \log \left(Z-c^T x\right)-\sum_{i=1}^n \log \left(x_i\right) \quad \text { over } x \in \mathbb{R}^n \ \text { subject to } A x=b, x>0, c^T x$ of $c^T x$. (i) Write down the KKT conditions for the minimization problem ().
(ii) By relating the KKT conditions from (i) to the conditions defining the primal central path, show that for a certain value of $\tau$ the solution of $\left{ }^{ *}\right)$ is situated on the primal central path.
For given $\theta \in(0,1)$, the problem of finding a value of the centering parameter $\sigma$ in the short-step path following algorithm that satisfies
$$
\frac{\theta^2+n(1-\sigma)^2}{2^{3 / 2}(1-\theta)} \leq \sigma \theta,
$$
while maximizing the decrease in the duality measure $\mu$ for a unit step can be posed as a simple constrained optimization problem. Write down this problem. Does this problem have a solution for all $\theta \in(0,1)$ ? Explain!
Consider the predictor-corrector and long-step path following algorithms. Prove that when $n=2$, the neighborhoods $\mathcal{N}2(\theta)$ and $\mathcal{N}{-\infty}(1-\theta / \sqrt{2})$ are identical. Does a similar relationship hold true when $n=3$ ?

MY-ASSIGNMENTEXPERT™可以为您提供MANOA.HAWAII MATH414 OPTIMIZATION THEORY最优化的代写代考和辅导服务!