MY-ASSIGNMENTEXPERT™可以为您提供manoa.hawaii MATH414 Optimization Theory最优化的代写代考和辅导服务!
这是夏威夷大学最优化的代写成功案例。
MATH414课程简介
Introduction to theory and methods for optimization. Topics may include least square analysis, search methods, conjugate direction methods, linear programming, integer programming, and constrained optimization. Pre: 243 or 253A, and 307 or 311; or consent.
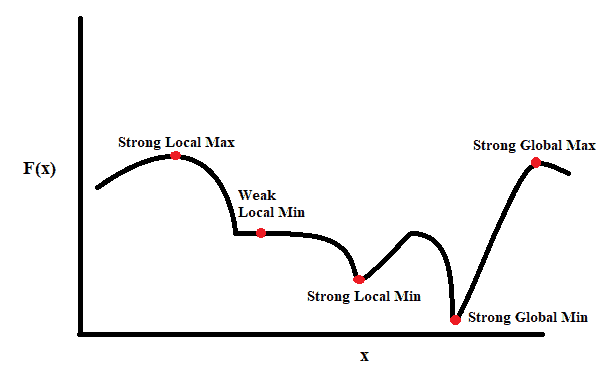
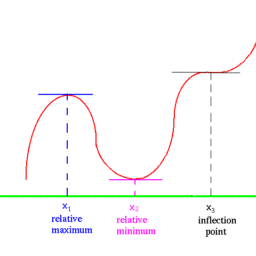
Mathematical optimization (alternatively spelled optimisation) or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives.[1] It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering[2] to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries
Prerequisites
In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding “best available” values of some objective function given a defined domain (or input), including a variety of different types of objective functions and different types of domains.
MATH414 Optimization Theory HELP(EXAM HELP, ONLINE TUTOR)
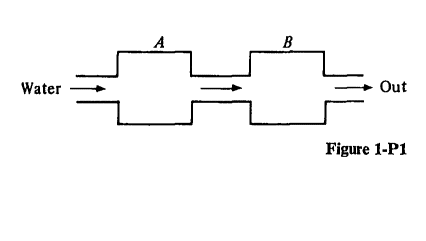
The tanks $A$ and $B$ shown in Fig. 1-P1 each have a capacity of 50 gal. Both tanks are filled at $t=0, \operatorname{tank} A$ with $60 \mathrm{lb}$ of salt dissolved in water, and $\operatorname{tank} B$ with water. Fresh water enters $\operatorname{tank} A$ at the rate of $8 \mathrm{gal} / \mathrm{min}$, the mixture of salt and water (assumed uniform) leaves $A$ and enters $B$ at the rate of $8 \mathrm{gal} / \mathrm{min}$, and the flow is incompressible. Let $q(t)$ and $p(t)$ be the number of pounds of salt contained in tanks $A$ and $B$, respectively.
(a) Write a set of state equations for the system.
(b) Draw a block diagram (or signal flow graph) for the system.
(c) Find the state transition matrix $\varphi(t)$.
(d) Determine $q(t)$ and $p(t)$ for $t \geq 0$.
(a) $d q(t) / d t=-.16 q(t) ; d p(t) / d t=.16 q(t)-.16 p(t)$
(c) $\varphi_{11}(t)=\epsilon^{-.16 t} ; \varphi_{12}(t)=0 . ; \varphi_{21}(t)=.16 t \epsilon^{-.16 t} ; \varphi_{22}(t)=\epsilon^{-.16 t}$
(d) $q(t)=60 \epsilon^{-16 t} ; p(t)=9.6 t \epsilon^{-16 t}, t \geq 0$.
(a) Write a set of state equations for the mechanical system shown in. Fig. 1-P3. The applied force is $f(t)$, the block has mass $M$, the spring constant is $K$, and the coefficient of viscous friction is $B$. The displacement of the block, $y(t)$, is measured from the equilibrium position with no force applied.
(b) Draw a block diagram (or signal flow graph) for the system.
(c) Let $M=1 \mathrm{~kg}, K=2 \mathrm{~N} / \mathrm{m}, B=2 \mathrm{~N} / \mathrm{m} / \mathrm{sec}$, and determine the state transition matrix $\varphi(t)$.
(d) If $y(0)=0.2 \mathrm{~m}, \dot{y}(0)=0$, and $f(t)=2 \epsilon^{-2 t} \mathrm{~N}$ for $t \geq 0$, determine $y(t)$ and $\dot{y}(t)$ for $t \geq 0$.
(a) $d y(t) / d t=\dot{y}(t) ; d \dot{y}(t) / d t=-K y(t) / M-B \dot{y}(t) / M+f(t) / M$
(c)
$$
\begin{aligned}
& \varphi_{11}(t)=\sqrt{2} \epsilon^{-t} \cos (t-\pi / 4) ; \varphi_{12}(t)=\epsilon^{-t} \sin t ; \varphi_{21}(t)=-2 \epsilon^{-t} \sin t \
& \varphi_{22}(t)=\sqrt{2} \epsilon^{-t} \cos (t+\pi / 4)
\end{aligned}
$$
(d)
$$
\begin{aligned}
& y(t)=2 \sqrt{2} \epsilon^{-t} \cos (t-\pi / 4)+\epsilon^{-2 t}+\sqrt{2} \epsilon^{-t} \cos (t-3 \pi / 4) \
& \dot{y}(t)=-4 \epsilon^{-t} \sin t-2 \epsilon^{-2 t}+2 \epsilon^{-t} \cos t
\end{aligned}
$$
Write state equations for the mechanical system in Fig. 1-P5. $\lambda$ is the applied torque, $I$ is the moment of inertia, $K$ is the spring constant, and $B$ is the coefficient of viscous friction. The angular displacement $\theta(t)$ is measured from the equilibrium position with no torque applied.
$d \theta(t) / d t=\dot{\theta}(t) ; d \dot{\theta}(t) / d t=-K \theta(t) / I-B \dot{\theta}(t) / I+\lambda(t) / I$.
Write a set of state equations for the electromechanical system shown in Fig. 1-P7. The amplifier gain is $K_a$, and the developed torque is $\lambda(t)=K_t i_f(t)$, where $K_a$ and $K_t$ are known constants.
$d i_f(t) / d t=-R_f i_f(t) / L_f+K_a e(t) / L_f ; d \omega(t) / d t=K_t i_f(t) / I-B \omega(t) / I$.

MY-ASSIGNMENTEXPERT™可以为您提供MANOA.HAWAII MATH414 OPTIMIZATION THEORY最优化的代写代考和辅导服务!