MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH2922 Regression Analysis回归分析课程的代写代考和辅导服务!
这是悉尼大学 回归分析课程的代写成功案例。

MATH2922课程简介
Linear and abstract algebra is one of the cornerstones of mathematics and it is at the heart of many applications of mathematics and statistics in the sciences and engineering. This unit is an advanced version of MATH2022, with more emphasis on the underlying concepts and on mathematical rigour. This unit investigates and explores properties of vector spaces, matrices and linear transformations, developing general principles relating to the solution sets of homogeneous and inhomogeneous linear equations, including differential equations. Linear independence is introduced as a way of understanding and solving linear systems of arbitrary dimension. Linear operators on real spaces are investigated, paying particular attention to the geometrical significance of eigenvalues and eigenvectors, extending ideas from first year linear algebra. To better understand symmetry, matrix and permutation groups are introduced and used to motivate the study of abstract groups theory. The unit culminates in studying inner spaces, quadratic forms and normal forms of matrices together with their applications to problems both in mathematics and in the sciences and engineering.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. appreciate the basic concepts and problems of linear algebra and be able to apply linear algebra to solve problems in mathematics, science and engineering
- LO2. understand the definitions of fields and vector spaces and be able to perform calculations in real and complex vector spaces, both algebraically and geometrically
- LO3. determine if a system of equations is consistent and find its general solution
- LO4. compute the rank of a matrix and understand how the rank of a matrix relates to the solution set of a corresponding system of linear equations
- LO5. compute the eigenvalues, eigenvectors, minimal polynomials and normal forms for linear transformations
- LO6. use the definition and properties of linear transformations and matrices of linear transformations and change of basis, including kernel, range and isomorphism
- LO7. compute inner products and determine orthogonality on vector spaces, including Gram-Schmidt orthogonalisation
- LO8. identify self-adjoint transformations and apply the spectral theorem and orthogonal decomposition of inner product spaces, and the Jordan canonical form, to solving systems of ordinary differential equations
- LO9. calculate the exponential of a matrix and use it to solve a linear system of ordinary differential equations with constant coefficients
- LO10. identify special properties of a matrix, such as symmetric of Hermitian, positive definite, etc., and use this information to facilitate the calculation of matrix characteristics
- LO11. demonstrate accurate and efficient use of advanced algebraic techniques and the capacity for mathematical reasoning through analysing, proving and explaining concepts from advanced algebra
- LO12. apply problem-solving using advanced algebraic techniques applied to diverse situations in physics, engineering and other mathematical contexts
MATH2922 Regression Analysis HELP(EXAM HELP, ONLINE TUTOR)
Give a prediction for the hardness that you would expect for an individual piece of plastic after 43 hours; give a $95 \%$ prediction interval for this quantity.
Solution: We predict a hardness of 256.1 after 43 hours; we are $95 \%$ confident that the hardness value will fall in the interval $[248.4,263.4]$.
Calculate power for the slope using the results of text Problem 1.22 as follows. Assume $n=16, \sigma^2=M S E$, and $S S_X=1280$.
(a) Find the power for rejecting the null hypothesis that the regression slope is zero using an $\alpha=0.05$ significance test when the alternative is $\beta_1=0.5$.
Solution: The power against $\mathrm{H}_A: \beta_1=0.5$ (calculated using SAS) is 0.99922 .
When testing whether or not $\beta_1=0$, why is the $F$ test a one-sided test even though $H_a$ includes both $\beta_1<0$ and $\beta_1>0$ ? [Hint: Refer to (2.57).]
Solution: The $F$-ratio is large when $\beta_1^2>0$, which is the same as testing whether $\beta_1>0$ or $\beta_1<0$.
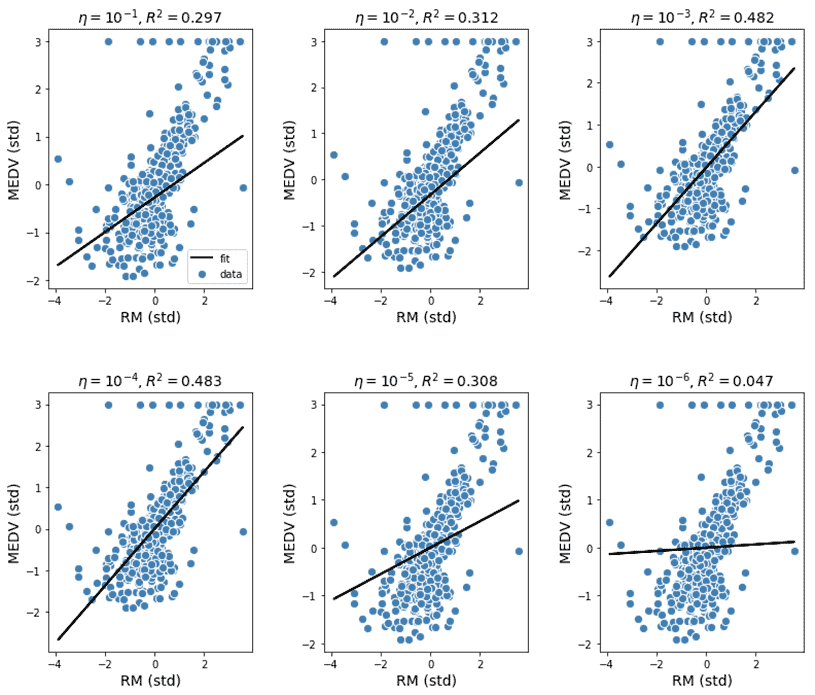
(b) Plot the power as a function of $\beta_1$ for values of $\beta_1$ between -2.5 and +2.5 in increments of 0.25 .
Solution: See the attached graph (Figure 4).
Given that $R^2=S S M / S S T$, it can be shown that $R^2 /\left(1-R^2\right)=S S M / S S E$. If you have $n=28$ cases and $R^2=0.3$, what is the $F$-statistic for the test that the slope is equal to zero?
Solution: The degrees of freedom are $d f_R=1$ and $d f_E=n-2=26$. The $F$-statistic is
$$
F=\frac{M S M}{M S E}=\frac{S S M / d f_M}{S S E / d f_E}=\frac{S S M}{S S E} \frac{d f_E}{d f_M}=\frac{R^2}{\left(1-R^2\right)} \frac{26}{1}=\frac{0.3 \times 26}{0.7}=11.14 .
$$
The $\alpha=0.05$ critical value for $F_{1,24}$ is 4.26 (from page 1322 ), and the $p$-value using that $d f$ is 0.0027 . The results for $F_{1,26}$ will be similar. We reject $\mathrm{H}_0: \beta_1=0$ and conclude that the slope it not zero.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH2922 REGRESSION ANALYSIS回归分析课程的代写代考和辅导服务!