MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH5340 Topology代数拓扑的代写代考和辅导服务!
这是悉尼大学拓扑学课程的成功案列。
MATH5340课程简介
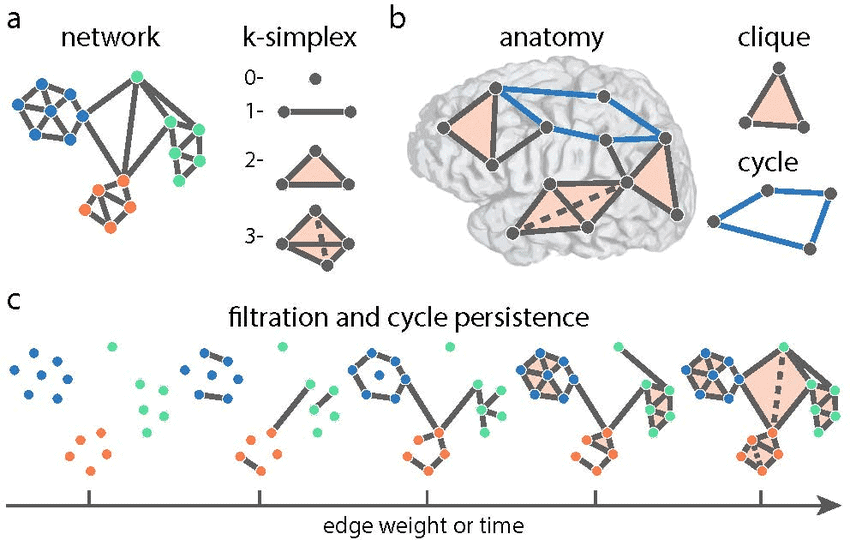
Topology is the mathematical theory of the “shape of spaces”. It gives a flexible framework in which the fabric of space is like rubber and thus enables the study of the general shape of a space. The spaces often arise indirectly: as the solution space of a set of equations; as the parameter space for a family of objects; as a point cloud from a data set; and so on. This leads to strong interactions between topology and a plethora of mathematical and scientific areas. The love of the study and use of topology is far reaching, including the use of topological techniques in the phases of matter and transition which received the 2016 Nobel Prize in Physics. This unit introduces you to a selection of topics in pure or applied topology. Topology receives strength from its areas of applications and imparts insights in return. A wide spectrum of methods is used, dividing topology into the areas of algebraic, computational, differential, geometric and set-theoretic topology. You will learn the methods, key results, and role in current mathematics of at least one of these areas, and gain an understanding of current research problems and open conjectures in the field.
Prerequisites
At the completion of this unit, you should be able to:
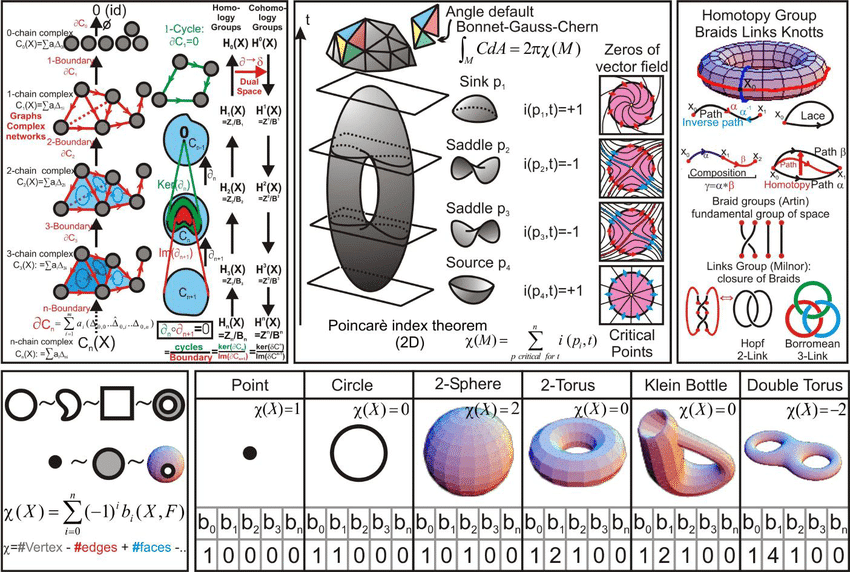
- LO1. Demonstrate a coherent and advanced understanding of the key concepts of fundamental group, covering spaces, homology and cohomology.
- LO2. Apply the fundamental principles and results of algebraic topology to solve given problems.
- LO3. Distinguish and compare the properties of different types of topological spaces and maps between them.
- LO4. Formulate topological problems in terms of algebraic invariants and determine the appropriate framework to solve them.
- LO5. Communicate coherent mathematical arguments appropriately to student and expert audiences, both orally and through written work.
- LO6. Devise computational solutions to complex problems in algebraic topology.
- LO7. Compose correct proofs of unfamiliar general results in algebraic topology.
MATH5340 Algebraic topology HELP(EXAM HELP, ONLINE TUTOR)
Given a set $X$ and a countable family $\mathcal{B}$ of subsets in $X$, denote by $\mathcal{T}$ the collection of subsets of $X$ that can be written as unions of elements of $\mathcal{B}$. Prove that for any family $\mathcal{A} \subset \mathcal{T}$ there is a countable subfamily $\mathcal{A}^{\prime} \subset \mathcal{A}$ such that
$$
\bigcup_{U \in \mathcal{A}^{\prime}} U=\bigcup_{V \in \mathcal{A}} V
$$
Hint: consider the family ${(U, V) \in \mathcal{B} \times \mathcal{A} \mid U \subset V}$.
(Zorn’s lemma) Let $(X, \leq)$ be a non-empty ordered set. If every chain in $X$ is upper bounded, then $X$ contains maximal elements.
We warn the young and inexperienced reader that the consequences of Zorn’s lemma are far more instructive than its proof. For this reason one might want to skip the proof at first. A proper argument, which requires the axiom of choice, will be given in Sect. 8.2, just for the sake of completeness.
Let’s show that the axiom of choice can be deduced from Zorn’s lemma. The proof we’ll provide is the most straightforward and useful means of applying Zorn’s lemma, whence we shall be very thorough. Consider the first version of the axiom of choice (V1), and let $X, Y$ be non-empty, $g: Y \rightarrow X$ onto. We’ll show that Zorn’s lemma yields the existence of a map $f: X \rightarrow Y$ such that $g(f(x))=x$ for every $x \in X$. For this let’s introduce the set $\mathcal{S}$ made by pairs $(E, f)$ where:
$E \subset X$ is a subset;
$f: E \rightarrow Y$ is such that $g f(x)=x$ for every $x \in E$.
The set $\mathcal{S}$ isn’t empty, for it contains the pair $(\emptyset, \emptyset \hookrightarrow Y)$. Elements in $\mathcal{S}$ can be ordered by extension: $(E, h) \leq(F, k)$ iff $k$ extends $h$, that is to say $E \subset F$ and $h(x)=k(x)$ for every $x \in E$. We claim that any chain $\mathcal{C} \subset \mathcal{S}$ is bounded from above. Consider the set
$$
A=\bigcup_{(E, h) \in \mathcal{C}} E
$$
and define $a: A \rightarrow Y$ like this: if $x \in A$ there is $(E, h) \in \mathcal{C}$ such that $x \in E$, and we set $a(x)=h(x)$. The map $a$ is well defined: if $(F, k) \in \mathcal{C}$ and $x \in F$ then $(E, h) \leq(F, k)$ or $(E, h) \geq(F, k)$ because $\mathcal{C}$ is a chain. In either case $x \in E \cap F$ and $h(x)=k(x)$. It is clear that $(A, a) \in \mathcal{S}$ is an upper bound for $\mathcal{C}$.
By Zorn’s lemma there is a maximal element $(U, f) \in \mathcal{S}$, so it suffices to show $U=X$. If that were not the case, there would exist $y \in Y$ such that $g(y) \notin U$ and the pair $\left(U \cup{g(y)}, f^{\prime}\right)$, extending $(U, f)$ and such that $f^{\prime}(g(y))=y$, would belong to $\mathcal{S}$, contradicting the maximality of $(U, f)$.
By Zorn’s lemma it suffices to show that each chain $\mathcal{C} \subset \mathcal{B}$ is upper bounded: to do that it’s enough to show
$$
\cup{A \mid A \in \mathcal{C}} \in \mathcal{B}
$$
If $B \subset \cup{A \mid A \in \mathcal{C}}$ is a finite subset, there exists $C \in \mathcal{C}$ such that $B \subset C$, and since $C \in \mathcal{B}$ we have $B \in \mathcal{B}$. This proves that any finite subset of $\cup{A \mid A \in \mathcal{C}}$ belongs to $\mathcal{B}$, whence $\cup{A \mid A \in \mathcal{C}} \in \mathcal{B}$.
Let $I$ be an infinite set, $\mathbb{K}$ a field and $\mathcal{B}$ a basis for the vector space $\mathbb{K}^I$ of maps $f: I \rightarrow \mathbb{K}$. Prove that the cardinality of $\mathcal{B}$ is strictly bigger than that of I. Deduce that every infinite-dimensional vector space cannot be isomorphic to its algebraic dual.
Hint: consider first the case where $\mathbb{K}$ is countable, using Exercise 2.30 . If $F$ is a subfield in $\mathbb{K}$, by the natural inclusion $F^I \subset \mathbb{K}^I$ every subset $A \subset F^I$ that is linearly independent over $F$ is also linearly independent over $\mathbb{K}$.
(There exist infinitely many primes, $\bigcirc$ ) For any pair of integers $a, b \in \mathbb{Z}$, with $b>0$, let’s write $N_{a, b}={a+k b \mid k \in \mathbb{Z}}$. Prove the following facts:
- arithmetic progressions $\mathcal{B}=\left{N_{a, b} \mid a, b \in \mathbb{Z}, b>0\right}$ form a basis for a topology $\mathcal{T}$ on $\mathbb{Z}$
- every $N_{a, b}$ is both open and closed in $\mathcal{T}$;
- call $P={2,3, \ldots} \subset \mathbb{N}$ the set of primes. Then
$$
\mathbb{Z}-{-1,1}=\cup\left{N_{0, p} \mid p \in P\right}
$$
Therefore if $P$ were finite ${-1,1}$ would be open in $\mathcal{T}$.
We need to show that the family of progressions $N_{a, b}$ satisfies Theorem 3.7: but this is an immediate consequence of the formulas
$$
N_{0,1}=\mathbb{Z}, \quad N_{a, b} \cap N_{c, d}=\cup\left{N_{s, b d} \mid s \in N_{a, b} \cap N_{c, d}\right}
$$
As $N_{a, b}$ is the complement in $\mathbb{Z}$ of the open union
$$
N_{a+1, b} \cup N_{a+2, b} \cup \ldots \cup N_{a+b-1, b}
$$
the open set $N_{a, b}$ is also closed. Note that any non-empty open set contains at least one arithmetic progression, and hence it must be infinite.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH5340 TOPOLOGY代数拓扑的代写代考和辅导服务!