数学代写|MATH1002 Linear Algebra

MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH1002 Linear Algebra线性代数的代写代考和辅导服务！

这是悉尼大学线性代数课程的代写成功案例。

MATH1002课程简介

MATH1002 is designed to provide a thorough preparation for further study in mathematics and statistics. It is a core unit of study providing three of the twelve credit points required by the Faculty of Science as well as a foundation requirement in the Faculty of Engineering. This unit of study introduces vectors and vector algebra, linear algebra including solutions of linear systems, matrices, determinants, eigenvalues and eigenvectors.

Prerequisites 

At the completion of this unit, you should be able to:

• LO1. apply mathematical logic and rigour to solving problems;
• LO2. represent vectors both algebraically and geometrically in two and three dimensions, and perform arithmetic with them;
• LO3. use vectors to solve classical geometric problems;
• LO4. determine spanning families and check linear independence
• LO5. perform and manipulate dot and cross products;
• LO6. set up systems of linear equations;
• LO7. solve systems of linear equations using Gaussian elimination;
• LO8. perform matrix arithmetic and calculate matrix inverses and determinants;
• LO9. find eigenvalues and eigenvectors;
• LO10. diagonalise a matrix;
• LO11. express mathematical ideas and arguments coherently in written form.

MATH1002 Linear algebra HELP（EXAM HELP， ONLINE TUTOR）

Solution
How do we solve these linear simultaneous equations, (1) and (2)?
Let’s think about the information contained in these equations. The $x$ in the first line represents the cost of an ice cream, so must have the same value as the $x$ in the second line. Similarly, the $y$ in the first line that represents the cost of a drink must have the same value as the $y$ in the second line.

It follows that we can combine the two equations to see if together they offer any useful information. How?
In this case, we subtract equation (2) from equation (1):
$$
\begin{gathered}
2 x+2 y=3 \
-(2 x+y=2.5) \
\hline 0+y=0.5
\end{gathered}
$$
Note that the unknown $x$ is eliminated in the last line which leaves $y=0.5$.
What else do we need to find?
The other unknown $x$.
How?
By substituting $y=0.5$ into equation (1):
$$
2 x+2(0.5)=3 \text { implies that } 2 x+1=3 \quad \text { gives } \quad x=1
$$
Hence the cost of an ice cream is $£ 1$ because $x=1$ and the cost of a drink is $£ 0.50$ because $y=0.5$; this is the solution to the given simultaneous equations (1) and (2).
This is also the point of intersection, $(1,0.5)$, of the graphs in Fig. 1.1. The procedure outlined in Example 1.1 is called the method of elimination. The values $x=1$ and $y=0.5$ is the solution of equations (1) and (2). In general, values which satisfy the above linear system are called the solution or the solution set of the linear system. Here is another example.

Solution
We need to find the values of $x$ and $y$ which satisfy both equations.
How?
Taking one equation from the other doesn’t help us here, but we can multiply through either or both equations by a non-zero constant.
If we multiply equation (1) by 2 and (2) by 9 then in both cases the $x$ coefficient becomes 18 . Carrying out this operation we have
$$
\begin{aligned}
& 18 x+6 y=12 {[\text { multiplying equation (1) by } 2] } \
& 18 x-63 y=81 \quad[\text { multiplying equation (2) by } 9]
\end{aligned}
$$
How do we eliminate $x$ from these equations?
To eliminate the unknown $x$ we subtract these equations:
$$
\begin{aligned}
18 x+6 y & =12 \
-(18 x-63 y & =81) \
0+[6-(-63)] y & =12-81 \quad[\text { subtracting] } \
69 y & =-69 \quad \text { which gives } y=-1
\end{aligned}
$$
We have $y=-1$.
What else do we need to find?
The value of the placeholder $x$.
How?
By substituting $y=-1$ into the given equation $9 x+3 y=6$ :
$$
\begin{aligned}
9 x+3(-1) & =6 \
9 x-3 & =6 \
9 x & =9 \text { which gives } x=1
\end{aligned}
$$
Hence our solution to the linear system of (1) and (2) is
$$
x=1 \text { and } y=-1
$$
We can check that this is the solution to the given system, (1) and (2), by substituting these values, $x=1$ and $y=-1$, into the equations (1) and (2).

Solution
What are we trying to find?
The values of $x, y$ and $z$ that satisfy all three equations (1), (2) and (3).
How do we find the values of $x, y$ and $z$ ?
By elimination. To eliminate one of these unknowns, we first need to make the coefficients of $x$ (or $y$ or $z$ ) equal.
Which one?
There are three choices but we select so that the arithmetic is made easier, in this case it is $x$. Multiply equation (1) by 2 and then subtract the bottom equation (3):
$$
\begin{aligned}
2 x+4 y+8 z=14 & \text { [multiplying (1) by } 2] \
-(2 x+3 y+3 z=1) & \text { (3) } \
0+y+5 z=13 & {[\text { subtracting }] }
\end{aligned}
$$

Note that we have eliminated $x$ and have the equation $y+5 z=13$.
How can we determine the values of $y$ and $z$ from this equation?
We need another equation with only $y$ and $z$.
How can we get this?
Multiply equation (1) by 3 and then subtract the second equation (2):
$$
\begin{aligned}
3 x+6 y+12 z & =21 & & {[\text { multiplying (1) by } 3] } \
-(3 x+7 y+2 z & =-11) & & \text { (2) } \
\hline 0-y+10 z & =32 & & {[\text { subtracting }] }
\end{aligned}
$$
[subtracting]
Again there is no $x$ and we have the equation $-y+10 z=32$.
How can we find $y$ and $z$ ?
We now solve the two simultaneous equations that we have obtained
$$
\begin{array}{r}
y+5 z=13 \
-y+10 z=32
\end{array}
$$
We add equations (4) and (5), because $y+(-y)=0$, which eliminates $y$.
$$
0+15 z=45 \text { gives } z=\frac{45}{15}=3
$$
Hence $z=3$, but how do we find the other two unknowns $x$ and $y$ ?
We first determine $y$ by substituting $z=3$ into equation (4) $y+5 z=13$ :
$$
\begin{array}{r}
y+(5 \times 3)=13 \
y+15=13 \quad \text { which gives } y=-2
\end{array}
$$

How do we solve these equations?
Multiply (1) by 2 and then subtract equation (2):
$$
\begin{aligned}
4 x+6 y=12 & \text { [Multiplying (1) by } 2] \
-(4 x+6 y=9) & \text { (2) } \
\hline 0+0=3 &
\end{aligned}
$$
But how can we have $0=3$ ?
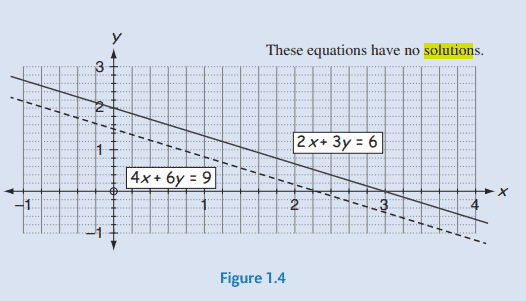
A plot of the graphs of the given equations is shown in Fig. 1.4.

Can you see why there is no common solution to these equations?
The solution of the given equations would be the intersection of the lines shown in Fig. 1.4, but these lines are parallel so there is no intersection, therefore no solution.
By examining the given equations,
$$
\begin{aligned}
& 2 x+3 y=6 \
& 4 x+6 y=9
\end{aligned}
$$
can you see why there is no solution?
If you multiply the first equation (1) by 2 we have
$$
4 x+6 y=12
$$
This is a contradiction.
Why?
Because we have
$$
\begin{aligned}
& 4 x+6 y=12 \
& 4 x+6 y=9
\end{aligned}
$$
that is, $4 x+6 y$ equals both 9 and 12. This is clearly impossible. Hence the given linear system has no solution.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH1002 LINEAR ALGEBRA线性代数的代写代考和辅导服务！