数学代写|MATH2069 Graph Theory

Lemma 0.1 (for Exercise 1a). Let $T_r(n)$ be the Turán graph and $t_r(n)$ the number of edges of $T_r(n)$. Then
$$
t_r(n+1)=t_r(n)+n-\left\lfloor\frac{n}{r}\right\rfloor
$$
Proof. We form $t_r(n+1)$ from $t_r(n)$ by adding a vertex $v$ to a group with $\left\lfloor\frac{n}{r}\right\rfloor$ vertices, then add all edges from $v$ to vertices from other groups. There are $n$ possible neighbors of $v$, but we must subtract the vertices from the same group. Thus we add $n-\left\lfloor\frac{n}{r}\right\rfloor$ edges.

Note: The right inequality in the following proposition was not part of Exercise 1a, but I needed it for $1 \mathrm{~b}$, and it was more economical to prove both inequalities in the same proposition.

Proposition 0.2 (Exercise 1a). Let $T_r(n)$ be the Turán graph and $t_r(n)$ the number of edges of $T_r(n)$. Then
$$
\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
n \
2
\end{array}\right) \leq t_r(n) \leq\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
n \
2
\end{array}\right)+n
$$
Proof. We prove both inequalities by induction on $n$. The base case $n=1$ holds because $\left(\begin{array}{l}1 \ 2\end{array}\right)=0$ and $t_r(1)=0$. Assume the left inequality holds for $n=1, \ldots, k$.
$$
\begin{aligned}
t_r(k+1) & =t_r(k)+k-\left\lfloor\frac{k}{r}\right\rfloor \geq\left(1-\frac{1}{r}\right)\left(\begin{array}{c}
k \
2
\end{array}\right)+\left(1-\frac{1}{r}\right) k \
& =\left(1-\frac{1}{r}\right)\left(\left(\begin{array}{l}
k \
2
\end{array}\right)+k\right)=\left(1-\frac{1}{r}\right)\left(\begin{array}{c}
k+1 \
2
\end{array}\right)
\end{aligned}
$$
This completes the proof of the first inequality. For the second inequality, note that
$$
k-\left\lfloor\frac{k}{r}\right\rfloor \leq k-\frac{k}{r}+1
$$

Then
$$
\begin{aligned}
t_r(k+1) & =t_r(k)+k-\left\lfloor\frac{k}{r}\right\rfloor \leq\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
k \
2
\end{array}\right)+k+k-\frac{k}{r}+1 \
& =\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
k \
2
\end{array}\right)+\left(1-\frac{1}{r}\right) k+(k+1)=\left(1-\frac{1}{r}\right)\left(\left(\begin{array}{l}
k \
2
\end{array}\right)+k\right)+(k+1) \
& =\left(1-\frac{1}{r}\right)\left(\begin{array}{c}
k+1 \
2
\end{array}\right)+(k+1)
\end{aligned}
$$
This completes the induction for the second inequality.

Proposition 0.3 (Exercise 1b). Let $t_r(n)$ be as above. Then for a fixed $r \geq 1$,
$$
t_r(n)=\frac{1}{2}\left(1-\frac{1}{r}\right) n^2+o\left(n^2\right) \quad \text { as } n \rightarrow \infty
$$
Proof. Using the first inequality from 1a,
$$
t_r(n)-\frac{1}{2}\left(1-\frac{1}{r}\right) n^2 \leq\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
n \
2
\end{array}\right)+n-\frac{1}{2}\left(1-\frac{1}{r}\right) n^2=\frac{1}{2}\left(1-\frac{1}{r}\right) n
$$
Using the second inequality from 1a,
$$
\frac{1}{2}\left(1-\frac{1}{r}\right) n^2-t_r(n) \leq \frac{1}{2}\left(1-\frac{1}{r}\right) n^2-\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
n \
2
\end{array}\right)=\frac{1}{2}\left(1-\frac{1}{r}\right) n
$$
Thus
$$
\left|t_r(n)-\frac{1}{2}\left(1-\frac{1}{r}\right) n^2\right| \leq \frac{1}{2}\left(1-\frac{1}{r}\right) n
$$
Thus for a fixed $r$, the error term is bounded above by a constant multiple of $n$. Thus for any $\epsilon>0$, for sufficiently large $n$ the error is bounded by $\epsilon n^2$. (Choose $n>\frac{c}{\epsilon}$ where $\left.c=\frac{1}{2}\left(1-\frac{1}{r}\right).\right)$

Theorem 0.4 (Exercise 3, Erdos-Simonovits Theorem). Let $F$ be a graph with chromatic number $r=\chi(F)$. Then
$$
\operatorname{ex}(F, n)=\frac{1}{2}\left(1-\frac{1}{r-1}\right) n^2+o\left(n^2\right)
$$
Proof. Since $\chi\left(T_{r-1}(n)\right)=r-1, T_{r-1}(n)$ does not contain $F$ as a subgraph. Thus
$$
\begin{aligned}
\operatorname{ex}(F, n) & \geq e\left(T_{r-1 n}(n)\right)=t_{r-1}(n) \geq\left(1-\frac{1}{r}\right)\left(\begin{array}{l}
n \
2
\end{array}\right) \geq\left(1-\frac{1}{r-1}\right)\left(\begin{array}{l}
n \
2
\end{array}\right) \
& =\left(1-\frac{1}{r-1}\right)\left(\frac{1}{2} n^2-\frac{1}{2} n\right) \geq \frac{1}{2}\left(1-\frac{1}{r-1}\right) n^2
\end{aligned}
$$
This is a sufficient lower bound for $\operatorname{ex}(F, n)$. Now we obtain an upper bound. We can restate the definition of $\operatorname{ex}(F, n)$ as
$$
\operatorname{ex}(F, n) \leq x \Longleftrightarrow(e(G) \geq x \Longrightarrow F \subset G)
$$
Let $\epsilon>0$. Then by Erdos-Stone, there exists $n_0$ such that for $n_0 \geq n$,
$$
e(G) \geq \frac{1}{2}\left(1-\frac{1}{r-1}+\epsilon\right) n^2 \Longrightarrow K_r(t) \subset G
$$
for some $t \geq \epsilon \log n /\left(2^{r+1}(r-1) !\right)$. Since $\chi(F)=r$, we know that $\chi(F) \subset K_r(t)$ for sufficiently large $t$, so $K_r(t) \subset G \Longrightarrow F \subset G$. Then by our equivalence (1), for $n \geq n_0$, we have
$$
\operatorname{ex}(F, n) \leq \frac{1}{2}\left(1-\frac{1}{r-1}+\epsilon\right) n^2=\frac{1}{2}\left(1-\frac{1}{r-1}\right) n^2+\frac{1}{2} \epsilon n^2
$$
Together, our two bounds say exactly that for $n \geq n_0$, we have
$$
\operatorname{ex}(F, n)=\frac{1}{2}\left(1-\frac{1}{r-1}\right) n^2+o\left(n^2\right)
$$
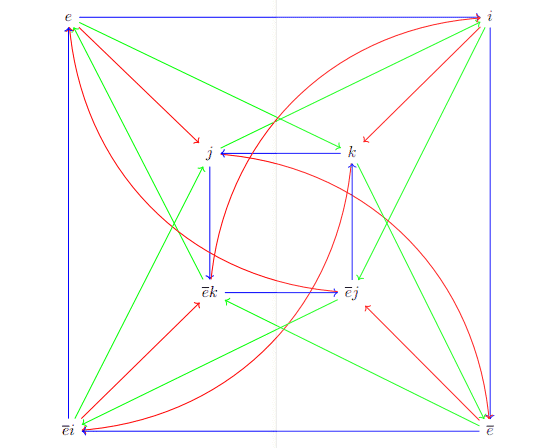
(Exercise 4) A presentation of the quaternion group $Q$ of order 8 is given by
$$
\left\langle\bar{e}, i, j, k \mid \bar{e}^2=1, i^2=j^2=k^2=i j k=\bar{e}\right\rangle
$$
It is clear from the relations that we do not need $\bar{e}$ or $k$ as a generator. From the relations, we can deduce that $\bar{e}$ commutes with everything and that
$$
i j=k \quad j i=k \quad k i=j \quad i k=\bar{e} j \quad j k=i \quad k j=\bar{e} i
$$
To show that this group has order 8 , we draw the Cayley graph of this presentation. Because $\bar{e}$ is in the center, it is relatively clear how multiplication by $\bar{e}$ acts, so we omit the $\bar{e}$ arrows. We could also omit the $k$ arrows, but we include them to better appreciate the symmetry.
Blue arrows are multiplication (on the right) by $i$, red arrows are multiplication (on the right) by $j$, and green arrows are multiplication (on the right) by $k$.