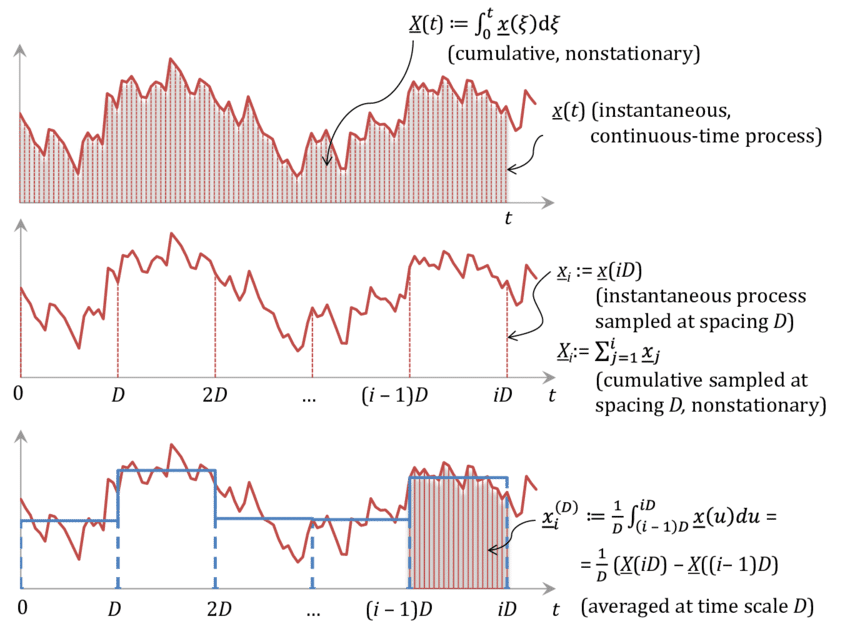
MY-ASSIGNMENTEXPERT™可以为您提供lse.ac.uk ST302 Stochastic processes随机过程课程的代写代考和辅导服务!
这是伦敦政经学校随机过程课程的代写成功案例。
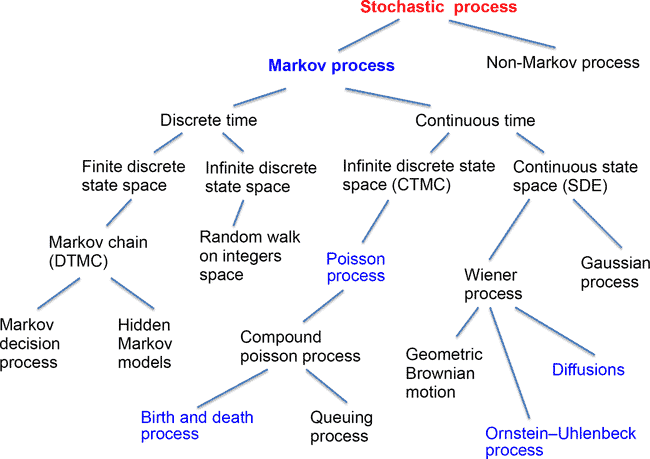
ST302课程简介
Availability
This course is compulsory on the BSc in Actuarial Science. This course is available on the BSc in Business Mathematics and Statistics, BSc in Data Science, BSc in Financial Mathematics and Statistics, BSc in Mathematics with Economics and BSc in Mathematics, Statistics and Business. This course is available as an outside option to students on other programmes where regulations permit and to General Course students.
Pre-requisites
Students must have completed either Probability, Distribution Theory and Inference (ST202) or Probability and Distribution Theory (ST206).
Prerequisites
Teaching
This course will be delivered through a combination of classes, lectures, and Q&A sessions totalling a minimum of 29 hours across Michaelmas Term.
The course includes a reading week in Week 6 of Michaelmas Term.
Formative coursework
Compulsory written answers to two sets of problems.
Indicative reading
Lecture notes will be provided. Relevant books include R Durrett, Essentials of Stochastic Processes; T Mikosch, Elementary Stochastic Calculus with Finance in View; Institute of Actuaries core reading notes.
ST302 Stochastic processes HELP(EXAM HELP, ONLINE TUTOR)
Consider the unit interval $I:=[0,1]$. Moreover, for every $n$ and $\left(i_1, \ldots, i_n\right) \in{0,1,2}^n$ we consider the interval $I_{i_1 \ldots i_n} \subset I$ which is the set of those numbers whose base 3 expansion starts with $\left(i_1 \ldots i_n\right)$. That is
$$
I_{i_1 \ldots i_n}:=\left[\sum_{k=1}^n \frac{i_k}{3^k}, \frac{1}{3^n}+\sum_{k=1}^n \frac{i_k}{3^k}\right] .
$$
Let $X_0, X_1, X_2$ be independent $\operatorname{Bernoulli}\left(p_0\right), \operatorname{Bernoulli}\left(p_1\right)$ and $\operatorname{Bernoulli}\left(p_2\right)$ random variables respectively. That is $\mathbb{P}\left(X_i=1\right)=p_i$ and $\mathbb{P}\left(X_i=0\right)=1-p_i$ for $i=0,1,2$. Moreover for every $n$ and $\left(i_1, \ldots, i_n\right) \in{0,1,2}^n$ we are given the random variables $X_{i_1 \ldots i_n}$ such that on the one hand $\left{X_{i_1 \ldots i_n}\right}_{n \geq 1,\left(i_1, \ldots, i_n\right) \in{0,1,2}^n}$ are independent and on the other hand: $X_{i_1 \ldots i_n} \stackrel{d}{=} X_{i_n}$. For every $n \geq 1$ we define the set $E_n \subset[0,1]$ by
$$
E_n:=\bigcup_{X_{i_1} \cdot X_{i_1, i_2} \cdots X_{i_1, i_2, \ldots, i_n}=1} I_{i_1 \ldots i_n} .
$$
Finally, we define the set $E:=\bigcap_{n=1}^{\infty} E_n$. Assume that $p_0=\frac{2}{3}, p_1=\frac{3}{4}$ and $p_2=\frac{1}{2}$. Question: Is it true that $\mathbb{P}(E \neq \emptyset)>0$
Given a branching process with the following offspring distribution, determine the extinction probabilities $q$ :
(a) $p_0=0.25, p_1=0.4, p_2=0.35, p_n=0$ if $n \geq 3$,
(b) $p_0=0.5, p_1=0.1, p_2=0, p_3=0.4, p_n=0$ if $n \geq 4$.
Consider the branching process with offspring distribution as in the previous exercise part (b). What is the probability that the population is extinct in the second generation $X_2=0$, given that it did not die out in the first generation?
Consider the branching process with offspring distribution given by $\left{p_n\right}_{n=0}^{\infty}$. We change this process into an irreducible Markov chain by the following modification:
whenever the population dies out, then the next generation has exactly one new individual. That is $\mathbb{P}\left(X_{n+1}=1 \mid X_n=0\right)=p(0,1)=1$. For which $\left{p_n\right}_{n=0}^{\infty}$ will this chain be null recurrent, recurrent, transient?
Let $X_1, X_2, \ldots$ i.i.d. random variables taking values in the integers such that $\mathbb{E}\left[X_i\right]=0$ for all $i$. Let $S_0:=0$ and $S_n:=X_1+\cdots+X_n$.
(a) Let $G_n(x):=\sum_{j=0}^n \mathbb{1}{\left{S_j=x\right}}$. That is $G_n(x)$ is the expected number of visits to $x$ in the first $n$ steps. Show that for all $n$ and $x, G_n(0) \geq G_n(x)$. (Hint: consider the first $j$ with $S_j=x$.) (b) Note that the Law of Large Numbers implies that for each $\varepsilon>0$ we have: $\lim {n \rightarrow \infty} \mathbb{P}\left(\left|S_n\right| \leq n \varepsilon\right)=1$. Using this prove that for each $\varepsilon>0$ we have $\lim {n \rightarrow \infty} \frac{1}{n} \sum{|x| \leq \varepsilon \cdot n, x \in \mathbb{Z}} G_n(x)=1$
(c) Using (a) and (b), show that for each $M<\infty$ there is an $n$ such that $G_n(0) \geq M$.
(d) Now prove that $S_n$ is a recurrent Markov chain.

MY-ASSIGNMENTEXPERT™可以为您提供LSE.AC.UK ST302 STOCHASTIC PROCESSES随机过程课程的代写代考和辅导服务!