MY-ASSIGNMENTEXPERT™可以为您提供cs.pitt.edu CS1699 Deep Learning深度学习课程的代写代考和辅导服务!
这是匹兹堡大学 深度学习课程代写成功案例。

CS1699课程简介
Location: Public Health G23
Time: Tuesday and Thursday, 3pm-4:15pm
Instructor: Adriana Kovashka (email: kovashka AT cs DOT pitt DOT edu; use “CS1699” at the beginning of the subject line)
Office: Sennott Square 5325
Office hours: Tuesday 12:20pm-1:30pm and 4:20pm-5:30pm; Thursday 10am-10:50am and 4:20pm-5:30pm
TA: Mingda Zhang (email: mzhang AT cs DOT pitt DOT edu; use “CS1699” at the beginning of the subject line)
TA’s office hours: Tuesday 9am-10am, Wednesday 10am-11am, Thursday 11:30am-12:30pm
TA’s office: Sennott Square 5503
Prerequisites: Math 220 (Calculus I), Math 280 or 1180 (Linear Algebra), CS 1501 (Algorithm Implementation)
Piazza: Sign up for it here. Please use Piazza rather than email so everyone can benefit from the discussion– you can post in such a way that only the instructor sees your name. Please try to answer each others’ questions whenever possible. The best time to ask the instructor or TA questions is during office hours.
Programming language/framework: We will use Python, NumPy/SciPy, and PyTorch.
Prerequisites
Overview
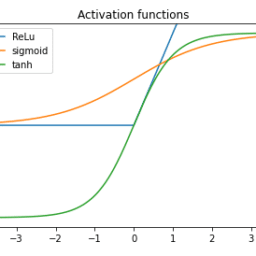
Course description: This course will cover the basics of modern deep neural networks. The first part of the course will introduce neural network architectures, activation functions, and operations. It will present different loss functions and describe how training is performed via backpropagation. In the second part, the course will describe specific types of neural networks, e.g. convolutional, recurrent, and graph networks, as well as their applications in computer vision and natural language processing. The course will also briefly discuss reinforcement learning and unsupervised learning, in the context of neural networks. In addition to attending lectures and completing bi-weekly homework assignments, students will also carry out and present a project.
CS1699 Deep Learning HELP(EXAM HELP, ONLINE TUTOR)
Problem 1. ( 5 points) Consider the function
$$
f(x, y)=\frac{1}{3}\left(x^2+3\right)^2+\frac{1}{2}\left(y^2+2\right)^2-4 x y^2-2 .
$$
a. What are the gradient and the Hessian of $f$ ?
b. Does the determinant of the gradient exist? If so, what is it?
c. Does the determinant of the Hessian exist? If so, what is it?
d. Use the gradient and Hessian to find and classify the critical points (i.e., local minima and maxima and saddle points, if any) for $f$.
e. Do global minima and/or maxima exist? If so, then what are they?
Problem 2. (10 points) Share code for the following problem as a working Jupyter notebook. Use Python 3 instead of Python 2.
a. Implement a gradient descent algorithm to find the local minima of $f$ from Problem 1 using the update function
$$
\left[x_{n+1}, y_{n+1}\right]^T=\left[x_n, y_n\right]^T-\gamma \nabla f\left(x_n, y_n\right),
$$
where $\left(x_n, y_n\right)$ is an approximation of a local minimum $\left(x^, y^\right)$ of $f$ after $n$ iterations of the update function.
b. Let $\gamma=10^{-3}$. For each local minimum $\left(x^, y^\right)$ of $f$, find a value of $\left(x_0, y_0\right)$ such that $\left|x_n-x^\right|+\left|y_n-y^\right|<10^{-6}$ for $n=10^6$. Are there any values of $\left(x_0, y_0\right)$ that do not converge to a local minimum of $f$ ?
c. Given $x_0, y_0$, and $\gamma$, find the number $n$ of iterations needed for $\left|x_n-x^\right|+\left|y_n-y^\right|<$ $10^{-6}$ for some local minimum $\left(x^, y^\right)$ of $f$. Plot, as a function of $\gamma \in\left[10^{-4}, 1\right]$, the expected number $n$ of iterations needed for $\left|x_n-x^\right|+\left|y_n-y^\right|<10^{-6}$ over the region $x_0, y_0 \in[-5,5]$, i.e., the average number of iterations needed for convergence over the region $[-5,5] \times[-5,5]$.
Problem 3. (5 points) An Emory student goes to one of the many Kaldi’s Coffee locations on campus and orders either hot or cold coffee at random.
In particular, suppose the the student goes to the coffee shop at the old train depot with probability $p$, the coffee shop at the new student center with probability $q$, and another coffee shop with probability $r$. Suppose, too, that if the student goes to the old train depot, then they order hot coffee with probability $s$, and if the student goes to the student center, then they order hot coffee with probability $t$.
What is the probability that the student goes to the coffee shop at the old train depot and orders hot coffee?
Problem 4. (10 points) Ronald Fisher’s Statistical Methods for Research Workers (1925) and The Design of Experiments (1935) were influential books for modern statistical methods and experimental design. This work either introduced or popularized the null hypothesis, $p$-values, the (problematic) convention of rejecting the null hypothesis for $p<0.05$, Fisher’s exact test, and certain randomized experiments. The lady tasting tea experiment from the second book is a classical example ${ }^1$ of a randomized experiment:
A LADY [sic] declares that by tasting a cup of tea made with milk she can discriminate whether the milk or the tea infusion was first added to the cup. We will consider the problem of designing an experiment by means of which this assertion can be tested. (Fisher, 1935, pp. 11)
Consider a machine learning version of this experiment. Suppose that there exists a database, $\mathrm{NISTea}^2$, with 10,000 labeled pictures of tea cups. In each picture, someone added either milk before tea or tea before milk to a cup, took a picture, and recorded whether milk or tea was added first. Suppose that you want to train and test a classifier for determining whether milk or tea was added first to a cup in a picture.
Write a short description (250-300 words) of a rigorous experimental design for evaluating your classifier. Do not write about how the classifier actually works, but assume that it has free/unknown parameters. (Hint: Use terms like data, evaluation, parameters, test, train, and validation.)

MY-ASSIGNMENTEXPERT™可以为您提供CS.PITT.EDU CS1699 DEEP LEARNING深度学习课程的代写代考和辅导服务