MY-ASSIGNMENTEXPERT™可以为您提供 hilbert Math541 Modern Algebra现代代数课程的代写代考和辅导服务!
这是威斯康星大学麦迪逊分校现代代数课程的代写成功案例。
Math541课程简介
- Definition and basic properties, subgroups.
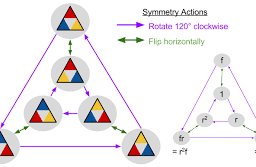
- Examples: Cyclic groups, matrix groups, unit groups, Dihedral groups, symmetric groups, etc.
- Group homomorphisms, cosets, normal subgroups, factor groups fundamental theorem of homomorphisms.
- Direct product and semi-product of groups.
- Cayley’s theorem, Lagrange theorem.
- Conjugacy classes, Sylow’s theorem, group action (if time permits).
Prerequisites
- Definition and basic properties, subrings.
- Examples: integers, Gausian integers, Z/n, polynomial rings, matrix algebra, etc.
- Ideals, quotient rings, ring homomorphisms, fundamental theorem of homomorphisms.
- Ideals, principal ideals, integral domains, PID, maximal and prime ideals
- Irreducible polynomials in a polynomial ring, division algorithm. Unique factorization, UFD.
Math541 Modern Algebra HELP(EXAM HELP, ONLINE TUTOR)
Solve problem 9 in Axler 10.A (p.305) for any finite-dimensional vector space $V$ over any field $F$. Note the corollary that the trace of $P$ is a nonnegative integer. [As I may have noted in lecture, operators satisfying $P^2=P$ (and thus $P^k=P$ for all $k=1,2,3, \ldots$, so the same as each power of $P)$ are called “idempotent”.]
Fix a nonnegative integer $k$. Let $F=\mathbf{R}$ or $\mathbf{C}$, and let $V / F$ be a vector space equipped with an inner product $\langle\cdot, \cdot\rangle$. For $v_1, \ldots, v_k, w_1, \ldots, w_k \in V$, define
$$
\left\langle\left\langle v_1 \wedge \cdots \wedge v_k, w_1 \wedge \cdots \wedge w_k\right\rangle\right\rangle
$$
to be the determinant of the $k \times k$ matrix whose $(i, j)$ entry is $\left\langle v_i, w_j\right\rangle$. Prove that $\langle\langle\cdot, \cdot\rangle\rangle$ extends to an inner product on the exterior power $\Lambda^k V$.
Let $V$ be a finite-dimensional vector space over a field $F$. For $\omega \in \Lambda^2 V$, define the rank of $\omega$ to be the rank of the associated alternating pairing on $V^$, which in turn is the rank of the corresponding map $V^ \rightarrow V$. [If $\omega=\sum_i a_i\left(v_i \wedge w_i\right)$, the pairing is given by
$$
\left.\left\langle v^, w^\right\rangle=\sum_i a_i\left(v^\left(v_i\right) w^\left(w_i\right)-v^\left(w_i\right) w^\left(v_i\right)\right) .\right]
$$
In Problem 7 of the last problem set we saw in effect that this rank is an even integer, say $2 k$. Use the results of that problem to give the following characterizations of $k$ :
i) For each $m=0,1,2, \ldots$, there exist $u_i, v_i \in V(i=1, \ldots, m)$ such that
$$
\omega=\sum_{i=1}^m u_i \wedge v_i
$$
if and only if $m \geq k$. Moreover, if $m=k$ then the $2 k$ vectors $u_i, v_i$ are linearly independent.
ii) In characteristic 0 or $p>2 k$, the $k$-th exterior power of $\omega$ (that is, the element $\omega \wedge \omega \wedge \cdots \wedge \omega$ of $\wedge^{2 k} V$, with $k$ factors of $\left.\omega\right)$ is nonzero, but the $(k+1)$-st exterior power vanishes.
And pfinally: A square matrix $A$ with entries $a_{i j}$ in a field $F$ is said to be skew-symmetric if its entries satisfy $a_{i j}=-a_{j i}$ for all $i, j$ and the diagonal entries $a_{i i}$ all vanish. We’ll show in class that $\operatorname{det} A=0$ if $A$ has odd order; here we study the even case.
If $A$ has even order $2 n$, and $n$ ! is invertible in $F$, the $\operatorname{Pfaffian} \operatorname{Pf}(A)$ can be defined thus: let $\omega \in \wedge^2\left(F^{2 n}\right)$ be defined by $\omega=\sum_{1 \leq i<j \leq 2 n} a_{i j} e_i \wedge e_j$; then $\operatorname{Pf}(A) \in F$ is the scalar such that
$$
\omega^n=n ! \operatorname{Pf}(A)\left(e_1 \wedge e_2 \wedge \cdots \wedge e_{2 n}\right)
$$
in $\wedge^{2 n}\left(F^{2 n}\right)$. (Of course $\omega^n$ means $\omega \wedge \omega \wedge \cdots \wedge \omega$ with $n$ factors.) Give an explicit formula for $\operatorname{Pf}(A)$ in terms of the $a_{i j}$, analogous to the formula for the determinant as a sum of $n$ ! monomials. Prove that
$$
\operatorname{det}(A)=(\operatorname{Pf}(A))^2 .
$$
This problem set is due Friday, 10 November, at the beginning of class.

MY-ASSIGNMENTEXPERT™可以为您提供 hilbert Math541 Modern Algebra现代代数课程的代写代考和辅导服务!