MY-ASSIGNMENTEXPERT™可以为您提供 hilbert Math541 Modern Algebra现代代数课程的代写代考和辅导服务!
这是威斯康星大学麦迪逊分校现代代数课程的代写成功案例。

Math541课程简介
- Definition and basic properties, subgroups.
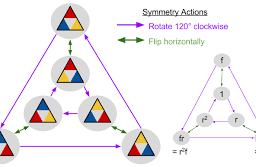
- Examples: Cyclic groups, matrix groups, unit groups, Dihedral groups, symmetric groups, etc.
- Group homomorphisms, cosets, normal subgroups, factor groups fundamental theorem of homomorphisms.
- Direct product and semi-product of groups.
- Cayley’s theorem, Lagrange theorem.
- Conjugacy classes, Sylow’s theorem, group action (if time permits).
Prerequisites
- Definition and basic properties, subrings.
- Examples: integers, Gausian integers, Z/n, polynomial rings, matrix algebra, etc.
- Ideals, quotient rings, ring homomorphisms, fundamental theorem of homomorphisms.
- Ideals, principal ideals, integral domains, PID, maximal and prime ideals
- Irreducible polynomials in a polynomial ring, division algorithm. Unique factorization, UFD.
Math541 Modern Algebra HELP(EXAM HELP, ONLINE TUTOR)
The rule $(s, t) \mapsto s+t$ for each ordered pair of real numbers $s$ and $t$ defines a mapping from the set of ordered pairs of real numbers to the set of real numbers. [That $(s, t)$ is ordered means that it is to be distinguished from $(t, s)$. The necessity for this distinction can be seen if addition is replaced by subtraction: $t-s \neq s-t$ unless $s=t$.] Mappings of this kind, assigning single elements of a set to pairs of elements from the same set, will be discussed at length in Section 3 .
If $\alpha: S \rightarrow T$ and $A$ is a subset of $S$, then $\alpha(A)$ will denote the set of elements of $T$ that are images of elements of $A$ under the mapping $\alpha$. In set-builder notation (described in Appendix A),
$$
\alpha(A)={\alpha(x): x \in A} .
$$
The set $\alpha(A)$ is called the image of $A$ under the mapping $\alpha$.
In terms of diagrams like those in Example 1.1, a mapping is onto provided each element of the codomain has at least one arrow pointing to it. Thus the mapping $\alpha$ in Example 1.1 is onto. However, the mapping $\beta$ in Example 1.1 is not onto; its image is ${1,3}$, which is a proper subset of ${1,2,3}$, the codomain of $\beta$.
With $f(x)=x^2$ and $g(x)=\sin x$ thought of as mappings from $\mathbb{R}$ to $\mathbb{R}$, neither is onto. The image of $f$ is the set of nonnegative real numbers. The image of $g$ is the set of real numbers between -1 and 1 , inclusive.
Definition. A mapping $\alpha: S \rightarrow T$ is said to be one-to-one if
$$
x_1 \neq x_2 \text { implies } \alpha\left(x_1\right) \neq \alpha\left(x_2\right) \quad\left(x_1, x_2 \in S\right),
$$
that is, if unequal elements in the domain have unequal images in the codomain.
In terms of diagrams like those in Example 1.1, a mapping is one-to-one provided no two arrows point to the same element. The mapping $\alpha$ in Example 1.1 is one-to-one. However, the mapping $\beta$ in Example 1.1 is not one-to-one, bécause $x \neq z$ but $\beta(x)=\beta(z)$.
With $f(x)=x^2$ and $g(x)=\sin x$ thought of as mappings from $\mathbb{R}$ to $\mathbb{R}$, neither is onto. The image of $f$ is the set of nonnegative real numbers. The image of $g$ is the set of real numbers between -1 and 1 , inclusive.
Definition. A mapping $\alpha: S \rightarrow T$ is said to be one-to-one if
$$
x_1 \neq x_2 \text { implies } \alpha\left(x_1\right) \neq \alpha\left(x_2\right) \quad\left(x_1, x_2 \in S\right),
$$
that is, if unequal elements in the domain have unequal images in the codomain.

MY-ASSIGNMENTEXPERT™可以为您提供 hilbert Math541 Modern Algebra现代代数课程的代写代考和辅导服务!