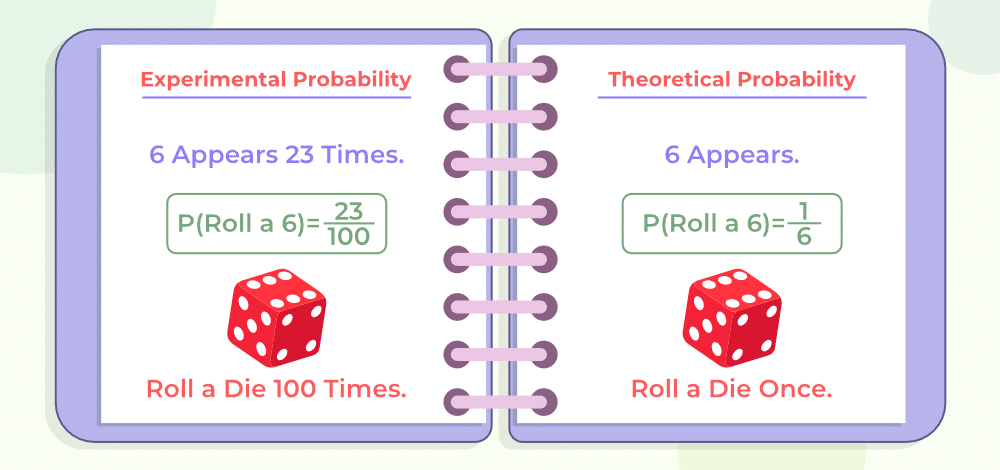
MY-ASSIGNMENTEXPERT™可以为您提供sydney STAT2011 Probability Theory概率论课程的代写代考和辅导服务!
这是悉尼大学概率论课程的代写成功案例。

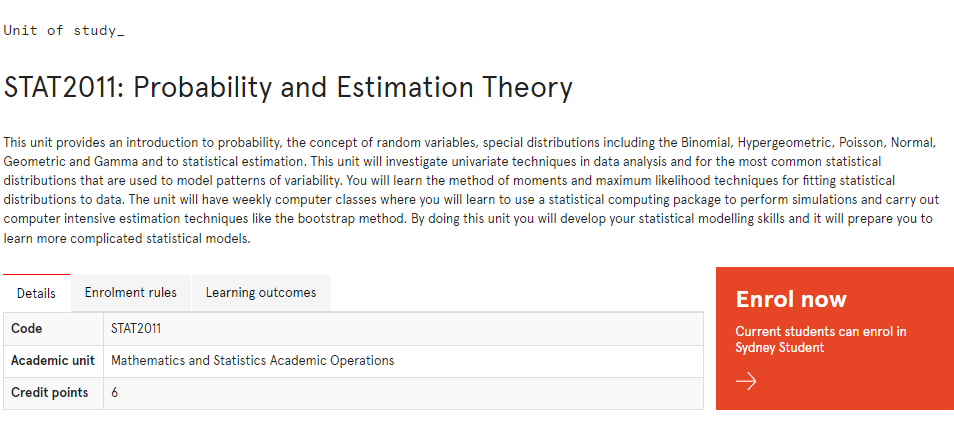
STAT2011课程简介
This unit provides an introduction to probability, the concept of random variables, special distributions including the Binomial, Hypergeometric, Poisson, Normal, Geometric and Gamma and to statistical estimation. This unit will investigate univariate techniques in data analysis and for the most common statistical distributions that are used to model patterns of variability. You will learn the method of moments and maximum likelihood techniques for fitting statistical distributions to data. The unit will have weekly computer classes where you will learn to use a statistical computing package to perform simulations and carry out computer intensive estimation techniques like the bootstrap method. By doing this unit you will develop your statistical modelling skills and it will prepare you to learn more complicated statistical models.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. construct appropriate statistical models involving random variables for a range of modelling scenarios. Compute (or approximate with a computer if necessary) numerical characteristics of random variables in these models such as probabilities, expectations and variances
- LO2. fit such models in outcome 1. to data (as appropriate) by estimating any unknown parameters
- LO3. compute appropriate (both theoretically and computationally derived) measures of uncertainty for any parameter estimates
- LO4. assess the goodness of fit (as appropriate) of a fitted model
- LO5. apply certain mathematical results (e.g. inequalities, limiting results) to problems relating to statistical estimation theory
- LO6. prove certain mathematical results (e.g. inequalities, limiting results) used in the course.
STAT2011 Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
As part of the game “Scrabble”, you draw tiles with letters on them from a bag. Let’s consider a scenarion in which the game is nearly over; there are four tiles in the bag, labeled “A”, ” $\mathrm{C}$ “, “G”, and “I”, and you are about to draw two of those tiles.
(a) Describe the sample space of this random experiment.
(b) You think you can win the game if you draw a vowel from the bag. Express the event “you draw a vowel” as a set of outcomes.
(c) What is the probability that you draw a vowel?
If a number between 1000 and 9999 is chosen uniformly at random, there is a $\frac{1}{100}$ chance that it is a palindrome (like 2772, for example) and a $\frac{1}{15}$ chance that it is divisible by 15 (like $2190=15 \cdot 146$, for example). Only three numbers in this range are both palindromes and divisible by 15 : they are 5115,5445 , and 5775 .
What is the probability that a number between 1000 and 9999 chosen uniformly at random is either a palindrome or divisible by 15 (or both)?
You are in a game show in which you’re asked a sequence of true/false questions. If you answer two of them wrong, you’re out!! Unfortunately, you have no idea what the answers are, so you guess randomly each time, and you have a $\frac{1}{2}$ chance of guessing the correct answer.
Let $A_3$ be the event that your first wrong answer is to the third question you are asked.
Let $B_4$ be the event that your second wrong answer is to the fourth question you are asked.
(a) Compute $\operatorname{Pr}\left[A_3\right]$.
(b) Compute $\operatorname{Pr}\left[A_3 \cap B_4\right]$.
(c) Compute $\operatorname{Pr}\left[B_4\right]$.
The flag of Greenland is shown below:
It is an $18 \times 12$ rectangle; if placed on a coordinate plane with bottom left corner at $(0,0)$ and top right corner at $(18,12)$, it is divided in half by a line at $y=6$ and has a circle of radius 4 centered at $(7,6)$.
The top half of the flag is white and the bottom half is red; within the circle, the two colors are swapped.
Suppose that a point on this flag is chosen uniformly at random.
(a) Find the probability that the chosen point is red.
(b) Find the probability that the chosen point is red or inside the circle. (As usual, “or” in mathematics includes the possibility that both things happen.)
MY-ASSIGNMENTEXPERT™可以为您提供sydney STAT2011 Probability Theory概率论课程的代写代考和辅导服务!