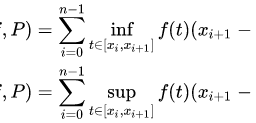0 0

By admin 数学代写 2022年2月23日

How bad can it get in terms of a continuous function not having a derivative at some points? It turns out it can be the case the function is nowhere differentiable but everywhere continuous. An example of such a pathological function different than the one I am about to present was discovered by Weierstrass in 1872 . However, Bolzano was the first to produce a function in the 1830 ‘s which was continuous and nowhere differentiable although he did not show this completely.

Lemma 7.4.1 Suppose $f^{\prime}(x)$ exists and let $c$ be a number. Then letting $g(x) \equiv$ $f(c x), \quad g^{\prime}(x)=c f^{\prime}(c x) .$

Here the derivative refers to either the derivative, the left derivative, or the right derivative. Also, if $f(x)=a+b x$, then
$$
f^{\prime}(x)=b
$$
where again, $f^{\prime}$ refers to either the left derivative, right derivative or derivative. Furthermore, in the case where $f(x)=a+b x$,
$$
f(x+h)-f(x)=b h .
$$
Proof: It is known from the definition that
$$
f(x+h)-f(x)-f^{\prime}(x) h=o(h)
$$
Therefore,
$$
g(x+h)-g(x)=f(c(x+h))-f(c x)=f^{\prime}(c x) c h+o(c h)
$$
134
CHAPTER. 7. THE DERIVATIVE $$ g(x+h)-g(x)-c f^{\prime}(c x) h=o(c h)=o(h) $$ oves the first part of the lemma. Now consider the last claim.
and so
and so this proves the first part of the lemma. Now consider the last claim.
$$
\begin{aligned}
f(x+h)-f(x) &=a+b(x+h)-(a+b x)=b h \
&=b h+0=b h+o(h) .
\end{aligned}
$$
Thus $f^{\prime}(x)=b$.
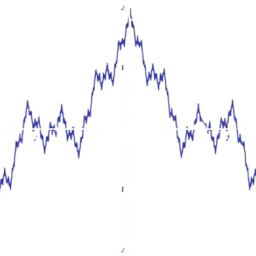
Now consider the following description of a function. The following is the graph of the function on $[0,1]$.
CCC(C)C
The height of the function is $1 / 2$ and the slope of the rising line is 1 while the slope of the falling line is $-1$. Now extend this function to the whole real line to make it periodic of period 1. This means $f(x+n)=f(x)$ for all $x \in \mathbb{R}$ and $n \in \mathbb{Z}$, the integers. In other words to find the graph of $f$ on $[1,2]$ you simply slide the graph of $f$ on $[0,1]$ a distance of 1 to get the same tent shaped thing on $[1,2]$. Continue this way. The following picture illustrates what a piece of the graph of this function looks like. Some might call it an infinite sawtonth
Now define
$$
g(x) \equiv \sum_{k=0}^{\infty}\left(\frac{3}{4}\right)^{k} f\left(4^{k} x\right)
$$
Letting $M_{k}=(3 / 4)^{-k}$, an application of the Weierstrass $M$ test shows $g$ is everywhere continuous. This is because each function in the sum is continuous and the series converges uniformly on $\mathbb{R}$.
Let $\delta_{m}=\pm \frac{1}{4}\left(4^{-m}\right)$ where we assume $m>2$. That of interest will be $m \rightarrow \infty$.
$$
\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}=\frac{\sum_{k=0}^{\infty}\left(\frac{3}{4}\right)^{k}\left(f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right)\right)}{\delta_{m}}
$$
If you take $k>m$,
$$
\begin{aligned}
f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right) &=f\left(4^{k}\left(x \pm \frac{1}{4}\left(4^{-m}\right)\right)\right)-f\left(4^{k} x\right) \
&=f\left(4^{k} x \pm \frac{1}{4} 4^{k-m}\right)-f\left(4^{k} x\right)=0
\end{aligned}
$$
Therefore,
$$
\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}=\frac{1}{\delta_{m}} \sum_{k=0}^{m}\left(\frac{3}{4}\right)^{k}\left(f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right)\right)
$$
The absolute value of the last term in the sum is
$$
\left|\left(\frac{3}{4}\right)^{m}\left(f\left(4^{m}\left(x+\delta_{m}\right)\right)-f\left(4^{m} x\right)\right)\right|
$$
7.5. FINDING THE DERIVATIVE and we choose the sign of $\delta_{m}$ such that both $4^{m}\left(x+\delta_{m}\right)$ and $4^{m} x$ are in ${[k / 2,(k+1) / 2)$ which is certainly possible because the distance betwee $} $ points is $1 / 4$ and such half open intervals inelude all of $\mathbb{R}$. Thus, since $f$ h on the interval just mentioned, $$ \left|\left(\frac{3}{4}\right)^{m}\left(f\left(4^{m}\left(x+\delta_{m}\right)\right)-f\left(4^{m} x\right)\right)\right|=\left(\frac{3}{4}\right)^{m} 4^{m}\left|\delta_{m}\right|=3^{m}\left|\delta_{m}\right| $$
135
and we choose the sign of $\delta_{m}$ such that both $4^{m}\left(x+\delta_{m}\right)$ and $4^{m} x$ are in some interval $[k / 2,(k+1) / 2)$ which is certainly possible because the distance between these two points is $1 / 4$ and such half open intervals include all of $\mathbb{R}$. Thus, since $f$ has slope $\pm 1$ on the interval just mentioned,
As to the other terms, $0 \leq f(x) \leq 1 / 2$ and so
$$
\left|\sum_{k=0}^{m-1}\left(\frac{3}{4}\right)^{k}\left(f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right)\right)\right| \leq \sum_{k=0}^{m-1}\left(\frac{3}{4}\right)^{k}=\frac{1-(3 / 4)^{m}}{1 / 4}=4-4\left(\frac{3}{4}\right)^{m}
$$
Thus
$$
\left|\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}\right| \geq 3^{m}-\left(4-4\left(\frac{3}{4}\right)^{m}\right) \geq 3^{m}-4
$$
Since $\delta_{m} \rightarrow 0$ as $m \rightarrow \infty, g^{\prime}(x)$ does not exist because the difference quotients are not bounded.
This proves the following theorem.
Theorem 7.4.2 There exists a function defined on $\mathbb{R}$ which is continuous and bounded but fails to have a derivative at any point.

在本节中，函数将在 $\mathbb{R}$ 的某个子集上定义，其值在 $\mathbb{F}$ 中。需要 $\mathbb{R}$ 的限制是因为我们要考虑单边限制。

在某些点没有导数的连续函数而言，它有多糟糕？事实证明，函数可能在任何地方都不可微，但在任何地方都是连续的。 Weierstrass 在 1872 年发现了一个与我将要介绍的不同的病理功能的例子。然而，Bolzano 是第一个在 1830 年代产生连续且无处可微的函数，尽管他没有完全展示这一点。

引理 7.4.1 假设 $f^{\prime}(x)$ 存在并且令 $c$ 是一个数字。然后让 $g(x) \equiv$ $f(c x), \quad g^{\prime}(x)=c f^{\prime}(c x) .$

这里的导数是指导数、左导数或右导数。另外，如果$f(x)=a+b x$，那么
$$
f^{\素数}(x)=b
$$
同样，$f^{\prime}$ 指的是左导数、右导数或导数。此外，在 $f(x)=a+b x$ 的情况下，
$$
f(x+h)-f(x)=b h 。
$$
证明：由定义可知
$$
f(x+h)-f(x)-f^{\prime}(x) h=o(h)
$$
所以，
$$
g(x+h)-g(x)=f(c(x+h))-f(c x)=f^{\prime}(c x) c h+o(ch)
$$
134
章节。 7. 导数 $$ g(x+h)-g(x)-c f^{\prime}(c x) h=o(ch)=o(h) $$ 超过引理的第一部分。现在考虑最后一个声明。
所以
所以这证明了引理的第一部分。现在考虑最后一个声明。
$$
\开始{对齐}
f(x+h)-f(x) &=a+b(x+h)-(a+b x)=b h \
&=b h+0=b h+o(h) 。
\end{对齐}
$$
因此$f^{\prime}(x)=b$。
现在考虑以下对函数的描述。下面是$[0,1]$上的函数图。
CCC(C)C
函数的高度为 $1 / 2$，上升线的斜率为 1，而下降线的斜率为 $-1$。现在将此函数扩展到整个实线，使其周期为 1。这意味着对于所有 $x \in \mathbb{R}$ 和 $n \in \，$f(x+n)=f(x)$ mathbb{Z}$，整数。换句话说，要在 $[1,2]$ 上找到 $f$ 的图形，您只需将 $[0,1]$ 上的 $f$ 图形滑动 1 的距离即可在 $[ 上得到相同的帐篷形状的东西。 1,2]$。继续这样。下图说明了该函数的图形的一部分。有些人可能会称之为无限锯齿
现在定义
$$
g(x) \equiv \sum_{k=0}^{\infty}\left(\frac{3}{4}\right)^{k} f\left(4^{k} x\right)
$$
令 $M_{k}=(3 / 4)^{-k}$，Weierstrass $M$ 检验的应用表明 $g$ 处处是连续的。这是因为 sum 中的每个函数都是连续的，并且级数一致地收敛于 $\mathbb{R}$。
假设 $\delta_{m}=\pm \frac{1}{4}\left(4^{-m}\right)$，我们假设 $m>2$。感兴趣的将是 $m \rightarrow \infty$。
$$
\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}=\frac{\sum_{k=0}^{\infty}\left(\frac {3}{4}\right)^{k}\left(f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right)\right)}{\delta_{m}}
$$
如果你取$k>m$，
$$
\开始{对齐}
f\left(4^{k}\left(x+\delta_{m}\right)\right)-f\left(4^{k} x\right) &=f\left(4^{k}\左(x \pm \frac{1}{4}\left(4^{-m}\right)\right)\right)-f\left(4^{k} x\right) \
&=f\left(4^{k} x \pm \frac{1}{4} 4^{k-m}\right)-f\left(4^{k} x\right)=0
\end{对齐}
$$
所以，
$$
\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}=\frac{1}{\delta_{m}} \sum_{k=0}^ {m}\left(\frac{3}{4}\right)^{k}\left(f\left(4^{k}\left(x+\delta_{m}\right)\right)-f \left(4^{k} x\right)\right)
$$
和中最后一项的绝对值为
$$
\left|\left(\frac{3}{4}\right)^{m}\left(f\left(4^{m}\left(x+\delta_{m}\right)\right)-f \left(4^{m} x\right)\right)\right|
$$
7.5。求导，我们选择 $\delta_{m}$ 的符号，使得 $4^{m}\left(x+\delta_{m}\right)$ 和 $4^{m} x$ 都在 ${[ k / 2,(k+1) / 2)$ 这当然是可能的，因为 $} $ 点之间的距离是 $1 / 4$ 并且这样的半开区间包括所有 $\mathbb{R}$。因此，由于 $f$ h 在刚刚提到的区间上，$$ \left|\left(\frac{3}{4}\right)^{m}\left(f\left(4^{m}\left (x+\delta_{m}\right)\right)-f\left(4^{m} x\right)\right)\right|=\left(\frac{3}{4}\right)^{ m} 4^{m}\left|\delta_{m}\right|=3^{m}\left|\delta_{m}\right| $$
135
我们选择 $\delta_{m}$ 的符号使得 $4^{m}\left(x+\delta_{m}\right)$ 和 $4^{m} x$ 都在某个区间 $[k / 2,(k+1) / 2)$ 这当然是可能的，因为这两个点之间的距离是 $1 / 4$ 并且这样的半开区间包括所有 $\mathbb{R}$。因此，由于 $f$ 在刚才提到的区间上有斜率 $\pm 1$，
至于其他条款，$0 \leq f(x) \leq 1 / 2$ 等等
$$
\left|\sum_{k=0}^{m-1}\left(\frac{3}{4}\right)^{k}\left(f\left(4^{k}\left(x+ \delta_{m}\right)\right)-f\left(4^{k} x\right)\right)\right| \leq \sum_{k=0}^{m-1}\left(\frac{3}{4}\right)^{k}=\frac{1-(3 / 4)^{m}}{ 1 / 4}=4-4\left(\frac{3}{4}\right)^{m}
$$
因此
$$
\left|\frac{g\left(x+\delta_{m}\right)-g(x)}{\delta_{m}}\right| \geq 3^{m}-\left(4-4\left(\frac{3}{4}\right)^{m}\right) \geq 3^{m}-4
$$
由于 $\delta_{m} \rightarrow 0$ as $m \rightarrow \infty，g^{\prime}(x)$ 不存在，因为差商是无界的。
这