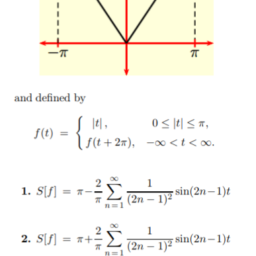
Infinite Series of Numbers
$5.1$ Basic Considerations
Earlier in Definition 4.4.1 on Page 54 the notion of limit of a sequence was discussed. There is a very closely related concept called an infinite series which is dealt with in this section.
Definition 5.1.1 Define
$$
\sum_{k=m}^{\infty} a_{k} \equiv \lim {n \rightarrow \infty} \sum{k=m}^{n} a_{k}
$$
whenever the limit exists and is finite. In this case the series is said to converge. If the series does not converge, it is said to diverge. The sequence $\left{\sum_{k=m}^{n} a_{k}\right}_{n-m}^{\infty}$ in the above is called the sequence of partial sums. This is always the definition. Here it is wnderstood that the a $_{k}$ are in $\mathrm{F}$, either $\mathbb{R}$ or $\mathbb{C}$ but it is the same definition in more general situations.
From this definition, it should be clear that infinite sums do not always make sense. Sometimes they do and sometimes they don’t, depending on the behavior of the partial sums. As an example, consider $\sum_{k-1}^{\infty}(-1)^{k}$. The partial sums corresponding to this symbol alternate between $-1$ and 0 . Therefore, there is no limit for the sequence of partial sums. It follows the symbol just written is meaningless and the infinite sum diverges.
Example 5.1.2 Find the infinite sum, $\sum_{n-1}^{\infty} \frac{1}{n(n+1)}$.
Note $\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$ and so $\sum_{n-1}^{N} \frac{1}{n(n+1)}=\sum_{n-1}^{N}\left(\frac{1}{n}-\frac{1}{n+1}\right)=-\frac{1}{N+1}+1$. Therefore, $\lim {N \rightarrow \infty} \sum{n-1}^{N} \frac{1}{n(n+1)}=\lim _{N \rightarrow \infty}\left(-\frac{1}{N+1}+1\right)=1$.
Proposition 5.1.3 Let $a_{k} \geq 0$. Then $\left{\sum_{k-m}^{n} a_{k}\right}_{n-m}^{\infty}$ is an increasing sequence. If this sequence is bounded above, then $\sum_{k-m}^{\infty} a_{k}$ converges and its value equals
$$
\sup \left{\sum_{k=-m}^{n} a_{k}: n=m, m+1, \cdots\right} .
$$
When the sequence is not bounded above, $\sum_{k-\mathrm{m}}^{\infty} a_{k}$ diverges.
Proof: It follows $\left{\sum_{k-m}^{n} a_{k}\right}_{n-m}^{\
infty}$ is an increasing sequence because $\sum_{k-m}^{n+1} a_
{k}-$ $\sum_{k-m}^{n} a_{k}=a_{n+1} \geq 0 .$ If it is bounded abo
ve, then by the form of completeness found $$ 77 $$
in Theorem $4.10 .2$ on Page 68 it follows the sequence of partial sums converges to $\sup \left{\sum_{k-m}^{n} a_{k}: n=m, m+1, \cdots\right}$. If the sequence of partial sums is not bounded, then it is not a Cauchy sequence and so it does not converge. See Theorem 4.5.3 on Page 57
In the case where $a_{k} \geq 0$, the above proposition shows there are only two alternatives available. Either the sequence of partial sums is bounded above or it is not bounded above. In the first case convergence occurs and in the second case, the infinite series diverges. For this reason, people will sometimes write $\sum_{k-\pi}^{\infty} a_{k}<\infty$ to denote the case where convergence occurs and $\sum_{k-m}^{\infty} a_{k}=\infty$ for the case where divergence occurs. Be very careful you never think this way in the case where it is not true that all $a_{k} \geq 0$. For example, the partial sums of $\sum_{k-1}^{\infty}(-1)^{k}$ are bounded because they are all either $-1$ or 0 but the series does not converge.
One of the most important examples of a convergent series is the geometric series. This series is $\sum_{-m=0}^{\infty} r^{n}$. The study of this series depends on simple high school algebra and Theorem $4.4 .11$ on Page 56 . Let $S_{n} \equiv \sum_{k=0}^{n} r^{k}$. Then
$$
S_{n}=\sum_{k=0}^{n} r^{k}, r S_{n}=\sum_{k=0}^{n} r^{k+1}=\sum_{k=1}^{n+1} r^{k}
$$ Therefore, subtracting the second equation from the first yields $(1-r) S_{n}=1-r^{n}+1.4$. and so a formula for $S_{n}$ is available. In fact, if $r \neq 1, S_{n}=\frac{1-r^{n+1}}{1-r}$.By Theorem $4.4$. lim $_{n \rightarrow \infty} S_{n}=\frac{1}{1-r}$ in the case when $|r|<1$. Now if $|r| \geq 1$, the limit clearly does not exist because $S_{n}$ fails to be a Cauchy sequence (Why?). This shows the following.
Theorem 5.1.4 The geometric series, $\sum_{n-0}^{\infty} r^{n}$ converges and equals $\frac{1}{1-r}$ if $|r|<1$ and diverges if $|r| \geq 1$.
If the series do converge, the following holds.
Theorem $5.1 .5$ If $\sum_{k-m}^{\infty} a_{k}$ and $\sum_{k-m}^{\infty} b_{k}$ both converge and $x, y$ are numbers, $$ \sum_{k=m}^{\infty} a_{k}=\sum_{k=m+j}^{\infty} a_{k-j} $$ $\sum_{k=m}^{\infty} x a_{k}+y b_{k}=x \sum_{k=m}^{\infty} a_{k}+y \sum_{k=m}^{\infty} b_{k}$ $\left|\sum_{k=m}^{\infty} a_{k}\right| \leq \sum_{k=m}^{\infty}\left|a_{k}\right|$
$$
\begin{gathered}
\sum_{k=\pi}^{\infty} x a_{k}+y b_{k}=x \sum_{k=m}^{\infty} a_{k}+y \sum_{k=m}^{\infty} b_{k} \
\left|\sum_{k=m}^{\infty} a_{k}\right| \leq \sum_{k=m}^{\infty}\left|a_{k}\right|
\end{gathered}
$$
where in the last inequality, the last sum equals $+\infty$ if the partial sums are not bounded above.
Proof: The above theorem is really only a restatement of Theorem $4.4 .8$ on Page 55 and the above definitions of infinite series. Thus
$$
\sum_{k=m}^{\infty} a_{k}=\lim {n \rightarrow \infty} \sum{k=m}^{n} a_{k}=\lim {n \rightarrow \infty} \sum{k-m+1}^{n+j} a_{k-j}=\sum_{k-m+j}^{\infty} a_{k-j}
$$
To establish $5.2$ use Theorem $4.4 .8$ on Page 55 to write
$$
\begin{aligned}
\sum_{k=m}^{\infty} x a_{k}+y b_{k} &=\lim {n \rightarrow \infty} \sum{k=m}^{n} x a_{k}+y b_{k}=\lim {n \rightarrow \infty}\left(x \sum{k=m}^{n} a_{k}+y \sum_{k=m}^{n} b_{k}\right) \
&=x \sum_{k=m}^{\infty} a_{k}+y \sum_{k=m}^{\infty} b_{k}
\end{aligned}
$$
微积分note5.1 Basic Considerations
无限数列
$5.1$ 基本注意事项
前面在第 54 页的定义 4.4.1 中讨论了序列极限的概念。本节将讨论一个非常密切相关的概念,称为无限级数。
定义 5.1.1 定义
$$
\sum_{k=m}^{\infty} a_{k} \equiv \lim {n \rightarrow \infty} \sum{k=m}^{n} a_{k}
$$
只要极限存在并且是有限的。在这种情况下,级数被称为收敛。如果级数不收敛,则称其发散。上面的序列$\left{\sum_{k=m}^{n} a_{k}\right}_{n-m}^{\infty}$称为部分和序列。这始终是定义。这里可以理解 a $_{k}$ 在 $\mathrm{F}$ 中,要么是 $\mathbb{R}$ 要么是 $\mathbb{C}$,但在更一般的情况下它是相同的定义。
根据这个定义,应该清楚的是,无限和并不总是有意义的。有时他们会,有时他们不会,这取决于部分和的行为。例如,考虑 $\sum_{k-1}^{\infty}(-1)^{k}$。与此符号对应的部分和在 $-1$ 和 0 之间交替。因此,部分和的顺序没有限制。它跟刚才写的符号毫无意义,无穷和发散。
例 5.1.2 求无穷和,$\sum_{n-1}^{\infty} \frac{1}{n(n+1)}$。
注意 $\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$ 等 $\sum_{n-1}^{N} \frac{1}{n(n(n+1)}=\sum_{n-1}^{N}\left(\frac{1}{n}-\frac{1}{n+1}\right) =-\frac{1}{N+1}+1$。因此,$\lim {N \rightarrow \infty} \sum{n-1}^{N} \frac{1}{n(n+1)}=\lim _{N \rightarrow \infty}\left (-\frac{1}{N+1}+1\right)=1$。
命题 5.1.3 令 $a_{k} \geq 0$。那么 $\left{\sum_{k-m}^{n} a_{k}\right}_{n-m}^{\infty}$ 是一个递增序列。如果这个序列在上面有界,那么 $\sum_{k-m}^{\infty} a_{k}$ 收敛并且它的值等于
$$
\sup \left{\sum_{k=-m}^{n} a_{k}: n=m, m+1, \cdots\right} 。
$$
当序列没有上界时,$\sum_{k-\mathrm{m}}^{\infty} a_{k}$ 发散。
证明:它遵循 $\left{\sum_{k-m}^{n} a_{k}\right}_{n-m}^{\
infty}$ 是一个递增序列,因为 $\sum_{k-m}^{n+1} a_
{k}-$ $\sum_{k-m}^{n} a_{k}=a_{n+1} \geq 0 .$ 如果有界 abo
ve,然后由完整性形式找到 $$ 77 $$
在第 68 页的定理 $4.10 .2$ 中,它遵循部分和的序列收敛到 $\sup \left{\sum_{km}^{n} a_{k}:n=m, m+1, \cdots\对}$。如果部分和的序列是无界的,那么它不是柯西序列,因此它不会收敛。见第 57 页的定理 4.5.3
在 $a_{k} \geq 0$ 的情况下,上述命题表明只有两种选择。部分和的序列要么有界,要么没有界。在第一种情况下发生收敛,在第二种情况下,无穷级数发散。出于这个原因,人们有时会写成 $\sum_{k-\pi}^{\infty} a_{k}<\infty$ 来表示发生收敛的情况,而 $\sum_{km}^{\infty} a_ {k}=\infty$ 用于发生分歧的情况。要非常小心,在所有 $a_{k} \geq 0$ 都不正确的情况下,你永远不要这样想。例如,$\sum_{k-1}^{\infty}(-1)^{k}$ 的部分和是有界的,因为它们都是 $-1$ 或 0,但级数不收敛。
收敛级数最重要的例子之一是几何级数。这个系列是 $\sum_{-m=0}^{\infty} r^{n}$。本系列的学习依赖于简单的高中代数和第 56 页上的定理 $4.4 .11$。令$S_{n} \equiv \sum_{k=0}^{n} r^{k}$。然后
$$
S_{n}=\sum_{k=0}^{n} r^{k}, r S_{n}=\sum_{k=0}^{n} r^{k+1}=\sum_{ k=1}^{n+1} r^{k}
$$ 因此,从第一个方程中减去第二个方程得到 $(1-r) S_{n}=1-r^{n}+1.4$。因此可以使用 $S_{n}$ 的公式。事实上,如果$r \neq 1,S_{n}=\frac{1-r^{n+1}}{1-r}$.由定理$4.4$。 lim $_{n \rightarrow \infty} S_{n}=\frac{1}{1-r}$ 在 $|r|<1$ 的情况下。现在如果 $|r| \geq 1$,显然不存在限制,因为 $S_{n}$ 不是柯西序列(为什么?)。这显示了以下内容。
定理 5.1.4 几何级数 $\sum_{n-0}^{\infty} r^{n}$ 收敛并等于 $\frac{1}{1-r}$ 如果 $|r|<1$如果 $|r| 则发散\geq 1$。
如果级数确实收敛,则以下成立。
定理 $5.1 .5$ 如果 $\sum_{km}^{\infty} a_{k}$ 和 $\sum_{km}^{\infty} b_{k}$ 都收敛并且 $x, y$ 是数字, $$ \sum_{k=m}^{\infty} a_{k}=\sum_{k=m+j}^{\infty} a_{kj} $$ $\sum_{k=m}^{\ infty} x a_{k}+y b_{k}=x \sum_{k=m}^{\infty} a_{k}+y \sum_{k=m}^{\infty} b_{k}$ $\left|\sum_{k=m}^{\infty} a_{k}\right| \leq \sum_{k=m}^{\infty}\left|a_{k}\right|$
$$
\开始{聚集}
\sum_{k=\pi}^{\infty} x a_{k}+y b_{k}=x \sum_{k=m}^{\infty} a_{k}+y \sum_{k=m }^{\infty} b_{k} \
\left|\sum_{k=m}^{\infty} a_{k}\right| \leq \sum_{k=m}^{\infty}\left|a_{k}\right|
\结束{聚集}
$$
其中在最后一个不等式中,如果部分和不受上述限制,则最后一个和等于 $+\infty$。
证明:上述定理实际上只是第 55 页上定理 $4.4 .8$ 的重述

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。