统计代写|How to count stat 代写
统计代考
Calculating the naive probability of an event $A$ involves counting the number of pebbles in $A$ and the number of pebbles in the sample space $S$. Often the sets we need to count are extremely large. This section introduces some fundamental methods for counting; further methods can be found in books on combinatorics, the branch of mathematics that studies counting.
1.4.1 Multiplication rule
In some problems, we can directly count the number of possibilities using a basic but versatile principle called the multiplication rule. We’ll see that the multiplication rule leads naturally to counting rules for sampling with replacement and sampling without replacement, two scenarios that often arise in probability and statistics.
Theorem 1.4.1 (Multiplication rule). Consider a compound experiment consisting of two sub-experiments, Experiment A and Experiment B. Suppose that Experiment A has $a$ possible outcomes, and for each of those outcomes Experiment B has $b$ possible outcomes. Then the compound experiment has $a b$ possible outcomes.
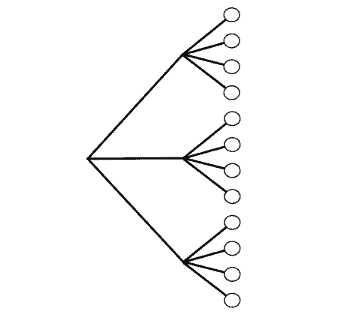
To see why the multiplication rule is true, imagine a tree diagram as in Figure 1.2. Let the tree branch $a$ ways according to the possibilities for Experiment A, and for each of those branches create $b$ further branches for Experiment B. Overall, there are $\underbrace{b+b+\cdots+b}_{a}=a b$ possibilities.
1.4.2. It is often easier to think about the experiments as being in chronological order, but there is no requirement in the multiplication rule that Experiment A has to be performed before Experiment $\mathrm{B}$.
Example 1.4.3 (Runners). Suppose that 10 people are running a race. Assume that ties are not possible and that all 10 will complete the race, so there will be welldefined first place, second place, and third place winners. How many possibilities are there for the first, second, and third place winners?
Solution: There are 10 possibilities for who gets first place, then once that is fixed there are 9 possibilities for who gets second place, and once these are both fixed there are 8 possibilities for third place. So by the multiplication rule, there are $10 \cdot 9 \cdot 8=720$ possibilities.
We did not have to consider the first place winner first. We could just as well have said that there are 10 possibilities for who got third place, then once that is fixed there are 9 possibilities for second place, and once those are both fixed there are 8 possibilities for first place. Or imagine that there are 3 platforms, which the first, second, and third place runners will stand on after the race. The platforms are gold, silver, and bronze, allocated to the first, second, and third place runners, respectively. Again there are $10 \cdot 9 \cdot 8=720$ possibilities for how the platforms will be occupied after the race, and there is no reason that the platforms must be considered in the order (gold, silver, bronze).
Example 1.4.4 (Chessboard). How many squares are there in an $8 \times 8$ chessboard, as in Figure $1.3 ?$ Even the name ” $8 \times 8$ chessboard” makes this easy: there are $8 \cdot 8=64$ squares on the board. The grid structure makes this clear, but we can also think of this as an example of the multiplication rule: to specify a square, we can specify which row and which column it is in. There are 8 choices of row, for each of which there are 8 choices of column.
Furthermore, we can see without doing any calculations that half the squares are white and half are black. Imagine rotating the chessboard 90 degrees clockwise. Then all the positions that had a white square now contain a black square, and vice versa, so the number of white squares must equal the number of black squares. We
统计代考
计算事件 $A$ 的天真概率涉及计算 $A$ 中的卵石数量和样本空间 $S$ 中的卵石数量。通常我们需要计算的集合非常大。本节介绍一些基本的计数方法;更多的方法可以在关于组合数学的书籍中找到,组合数学是研究计数的数学分支。
1.4.1 乘法规则
在某些问题中,我们可以使用称为乘法规则的基本但通用的原理直接计算可能性的数量。我们将看到,乘法规则自然会导致有放回抽样和无放回抽样的计数规则,这两种情况经常出现在概率和统计中。
定理 1.4.1(乘法规则)。考虑一个由两个子实验组成的复合实验,实验 A 和实验 B。假设实验 A 有 $a$ 个可能的结果,并且对于这些结果中的每一个,实验 B 有 $b$ 个可能的结果。那么复合实验就有$a b$可能的结果。
要了解为什么乘法规则是正确的,请想象一个如图 1.2 所示的树形图。根据实验 A 的可能性让树分支 $a$ 路,并为每个分支为实验 B 创建 $b$ 更多分支。总体而言,有 $\underbrace{b+b+\cdots+b}_{ a}=ab$ 的可能性。
1.4.2.通常更容易将实验视为按时间顺序排列,但乘法规则中没有要求实验 A 必须在实验 $\mathrm{B}$ 之前执行。
示例 1.4.3(跑步者)。假设有 10 个人在赛跑。假设不可能出现平局,并且所有 10 人都将完成比赛,因此将有明确的第一名、第二名和第三名获胜者。一、二、三等奖有多少种可能?
解:第一名有10种可能性,一旦确定了第二名就有9种可能性,如果都确定了第三名就有8种可能性。所以根据乘法规则,有 $10 \cdot 9 \cdot 8=720$ 的可能性。
我们不必首先考虑第一名的获胜者。我们也可以说,谁获得第三名有 10 种可能性,那么一旦确定了第二名的可能性,就有 9 种可能性,一旦两者都确定了,就有 8 种可能性获得第一名。或者想象有 3 个平台,一、二、三名选手在赛后会站在上面。平台是金、银和铜牌,分别分配给第一名、第二名和第三名选手。同样有 $10 \cdot 9 \cdot 8=720$ 的可能性来决定如何在比赛结束后占据平台,并且没有理由必须按顺序(金、银、铜)考虑平台。
示例 1.4.4(棋盘)。 $8 \times 8$ 棋盘中有多少个方格,如图 $1.3 ?$ 甚至名称“$8 \times 8$ chessboard”也很容易:棋盘上有 $8 \cdot 8=64$ 个方格。网格结构清楚地表明了这一点,但我们也可以将其视为乘法规则的一个示例:指定一个正方形,我们可以指定它在哪一行和哪一列。行有 8 种选择,每一种列有 8 种选择。
此外,我们无需进行任何计算就可以看到一半的正方形是白色的,一半是黑色的。想象一下将棋盘顺时针旋转 90 度。那么所有有白色方块的位置现在都包含一个黑色方块,反之亦然,所以白色方块的数量必须等于黑色方块的数量。我们
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。