统计代写|Random variables stat代写
统计代考
To see why our current notation can quickly become unwieldy, consider again the gambler’s ruin problem from Chapter 2 . In this problem, we may be very interested in how much wealth each gambler has at any particular time. So we could make up notation like letting $A_{j k}$ be the event that gambler A has exactly $j$ dollars after $k$ rounds, and similarly defining an event $B_{j k}$ for gambler $\mathrm{B}$, for all $j$ and $k$.
This is already too complicated. Furthermore, we may also be interested in other quantities, such as the difference in their wealths (gambler A’s minus gambler B’s) after $k$ rounds, or the duration of the game (the number of rounds until one player is bankrupt). Expressing the event “the duration of the game is $r$ rounds” in terms of the $A_{j k}$ and $B_{j k}$ would involve a long, awkward string of unions and intersections. And then what if we want to express gambler A’s wealth as the equivalent amount in euros rather than dollars? We can multiply a number in dollars by a currency exchange rate, but we can’t multiply an event by an exchange rate.
Instead of having convoluted notation that obscures how the quantities of interest are related, wouldn’t it be nice if we could say something like the following?
Let $X_{k}$ be the wealth of gambler A after $k$ rounds. Then $Y_{k}=N-X_{k}$ is the wealth of gambler B after $k$ rounds (where $N$ is the fixed total wealth); $X_{k}-Y_{k}=2 X_{k}-N$ is the difference in wealths after $k$ rounds; $c_{k} X_{k}$ is the wealth of gambler $\mathrm{A}$ in euros after $k$ rounds, where $c_{k}$ is the euros per dollar exchange rate after $k$ rounds; and the duration is $R=\min \left{n: X_{n}=0\right.$ or $\left.Y_{n}=0\right}$.
The notion of a random variable will allow us to do exactly this! It needs to be introduced carefully though, to make it both conceptually and technically correct. Sometimes a definition of “random variable” is given that is a barely paraphrased
104
103
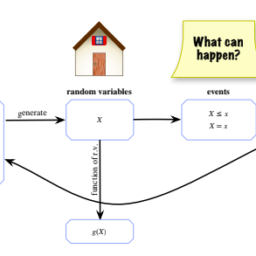
version of “a random variable is a variable that takes on random values”, but such a feeble attempt at a definition fails to say where the randomness come from. Nor does it help us to derive properties of random variables: we’re familiar with working with algebraic equations like $x^{2}+y^{2}=1$, but what are the valid mathematical operations if $x$ and $y$ are random variables? To make the notion of random variable precise, we define it as a function mapping the sample space to the real line. (See the math appendix for review of some concepts about functions.)
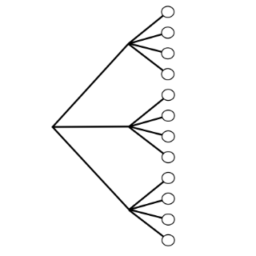
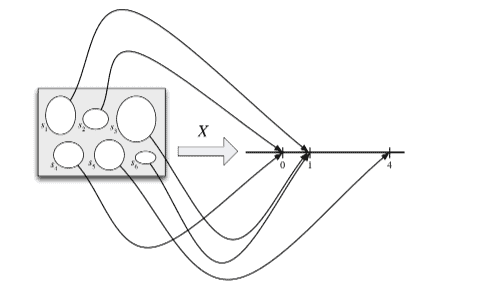
FIGURE $3.1$
A random variable maps the sample space into the real line. The r.v. $X$ depicted here is defined on a sample space with 6 elements, and has possible values 0,1 , and 4. The randomness comes from choosing a random pebble according to the probability function $P$ for the sample space.
Definition 3.1.1 (Random variable). Given an experiment with sample space $S$, a random variable (r.v.) is a function from the sample space $S$ to the real numbers $\mathbb{R}$. It is common, but not required, to denote random variables by capital letters.
Thus, a random variable $X$ assigns a numerical value $X(s)$ to each possible outcome $s$ of the experiment. The randomness comes from the fact that we have a random experiment (with probabilities described by the probability function P); the mapsimpler way in the left panel of Figure $3.2$, in which we inscribe the values inside the pebbles.
This definition is abstract but fundamental; one of the most important skills to develop when studying probability and statistics is the ability to go back and forth between abstract ideas and concrete examples. Relatedly, it is important to work on recognizing the essential pattern or structure of a problem and how it connects
Random variables and their distributions
105
to problems you have studied previously. We will often discuss stories that involve tossing coins or drawing balls from urns because they are simple, convenient scenarios to work with, but many other problems are isomorphic: they have the same essential structure, but in a different guise.
To start, let’s consider a coin-tossing example. The structure of the problem is that we have a sequence of trials where there are two possible outcomes for each trial. Here we think of the possible outcomes as $H$ (Heads) and $T$ (Tails), but we could just as well think of them as “success” and “failure” or as 1 and 0 , for example.
Example 3.1.2 (Coin tosses). Consider an experiment where we toss a fair coin twice. The sample space consists of four possible outcomes: $S=$ ${H H, H T, T H, T T}$. Here are some random variables on this space (for practice, you can think up some of your own). Each r.v. is a numerical summary of some aspect of the experiment.
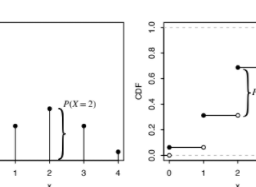
- Let $X$ be the number of Heads. This is a random variable with possible values 0 , 1 , and 2. Viewed as a function, $X$ assigns the value 2 to the outcome $H H, 1$ to the outcomes $H T$ and $T H$, and 0 to the outcome TT. That is,
$$
X(H H)=2, X(H T)=X(T H)=1, X(T T)=0 .
$$ - Let $Y$ be the number of Tails. In terms of $X$, we have $Y=2-X$. In other words, $Y$ and $2-X$ are the same r.v.: $Y(s)=2-X(s)$ for all $s$.
- Let $I$ be 1 if the first toss lands Heads and 0 otherwise. Then $I$ assigns the value 1 to the outcomes $H H$ and $H T$ and 0 to the outcomes $T H$ and TT. This r.v. is an example of what is called an indicator random variable since it indicates whether the first toss lands Heads, using 1 to mean “yes” and 0 to mean “no”.
We can also encode the sample space as ${(1,1),(1,0),(0,1),(0,0)}$, where 1 is the code for Heads and 0 is the code for Tails. Then we can give explicit formulas for $X, Y, I$
$$
X\left(s_{1}, s_{2}\right)=s_{1}+s_{2}, Y\left(s_{1}, s_{2}\right)=2-s_{1}-s_{2}, I\left(s_{1}, s_{2}\right)=s_{1},
$$
where for simplicity we write $X\left(s_{1}, s_{2}\right)$ to mean $X\left(\left(s_{1}, s_{2}\right)\right)$, etc.
For most r.v.s we will consider, it is tedious or infeasible to write down an explicit formula in this way. Fortunately, it is usually unnecessary to do so, since (as we saw in this example) there are other ways to define an r.v., and (as we will see throughout the rest of this book) there are many ways to study the properties of each outcome $s$ to.
As in the previous chapters, for a sample space with a finite number of outcomes we can visualize the outcomes as pebbles, with the mass of a pebble corresponding to its probability, such that the total mass of the pebbles is 1 . A random variable simply labels each pebble with a number. Figure $3.2$ shows two random variables
统计代考
要了解为什么我们当前的符号会很快变得笨拙,请再次考虑第 2 章中的赌徒破产问题。在这个问题中,我们可能对每个赌徒在任何特定时间拥有多少财富非常感兴趣。所以我们可以组成符号,比如让 $A_{jk}$ 是赌徒 A 在 $k$ 轮之后恰好有 $j$ 美元的事件,并且类似地为赌徒 $\mathrm{B 定义一个事件 $B_{jk}$ }$,对于所有的 $j$ 和 $k$。
这已经太复杂了。此外,我们还可能对其他数量感兴趣,例如在 $k$ 回合后他们的财富差异(赌徒 A 减去赌徒 B),或者游戏的持续时间(直到一个玩家破产的回合数)。用 $A_{j k}$ 和 $B_{j k}$ 表示事件“游戏的持续时间是 $r$ 轮”将涉及一长串尴尬的联合和交叉。那么如果我们想将赌徒 A 的财富表示为等值的欧元而不是美元呢?我们可以将美元数乘以货币汇率,但不能将事件乘以汇率。
与其使用复杂的符号来掩盖感兴趣的数量之间的关系,不如说像下面这样的话不是很好吗?
设 $X_{k}$ 是赌徒 A 在 $k$ 轮之后的财富。那么$Y_{k}=N-X_{k}$是赌徒B在$k$轮后的财富(其中$N$是固定的总财富); $X_{k}-Y_{k}=2 X_{k}-N$是$k$轮后的财富差; $c_{k} X_{k}$ 是赌徒 $\mathrm{A}$ 在 $k$ 轮之后以欧元计的财富,其中 $c_{k}$ 是在 $k$ 轮之后欧元兑美元汇率;持续时间为 $R=\min \left{n: X_{n}=0\right.$ 或 $\left.Y_{n}=0\right}$。
随机变量的概念将使我们能够做到这一点!但是,需要仔细介绍它,以使其在概念上和技术上都正确。有时给出的“随机变量”定义几乎没有解释
104
103
“随机变量是一个具有随机值的变量”的版本,但是对定义的这种微弱尝试未能说明随机性来自何处。它也不能帮助我们推导出随机变量的性质:我们熟悉代数方程,如 $x^{2}+y^{2}=1$,但是如果 $x$ 和$y$ 是随机变量吗?为了使随机变量的概念更精确,我们将其定义为将样本空间映射到实线的函数。 (有关函数的一些概念的回顾,请参见数学附录。)
图 $3.1$
随机变量将样本空间映射到实线。房车此处描述的 $X$ 是在具有 6 个元素的样本空间上定义的,并且具有可能的值 0,1 和 4。随机性来自根据样本空间的概率函数 $P$ 选择随机卵石。
定义 3.1.1(随机变量)。给定样本空间 $S$ 的实验,随机变量 (r.v.) 是从样本空间 $S$ 到实数 $\mathbb{R}$ 的函数。用大写字母表示随机变量是常见的,但不是必需的。
因此,随机变量 $X$ 将数值 $X(s)$ 分配给实验的每个可能结果 $s$。随机性来自于我们有一个随机实验(概率由概率函数 P 描述);图 $3.2$ 左侧面板中的 mapsimpler 方式,我们在其中将值刻在鹅卵石内。
这个定义是抽象但基本的;在学习概率和统计学时,最重要的技能之一是在抽象概念和具体例子之间来回切换的能力。相关地,重要的是要努力识别问题的基本模式或结构以及它是如何联系起来的
随机变量及其分布
105
对于你之前研究过的问题。我们会经常讨论抛硬币或从瓮中抽球的故事,因为它们是简单、方便的场景,但许多其他问题是同构的:它们具有相同的基本结构,但形式不同。
首先,让我们考虑一个抛硬币的例子。问题的结构是我们有一系列试验,其中每个试验有两种可能的结果。在这里,我们将可能的结果视为 $H$(正面)和 $T$(反面),但我们也可以将它们视为“成功”和“失败”或 1 和 0 等。
示例 3.1.2(抛硬币)。考虑一个实验,我们将一枚公平的硬币抛两次。样本空间由四种可能的结果组成:$S=$${H H, H T, T H, T T}$。这里有一些关于这个空间的随机变量(为了练习,你可以自己想出一些)。每个房车是实验某些方面的数字总结。
- 设 $X$ 为正面数。这是一个随机变量,可能值为 0 、 1 和 2。作为一个函数,$X$ 将值 2 分配给结果 $HH,将 1$ 分配给结果 $HT$ 和 $TH$,并将 0 分配给结果
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。