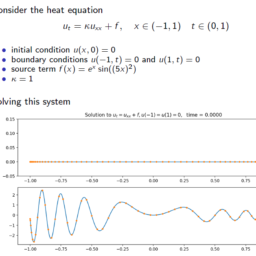
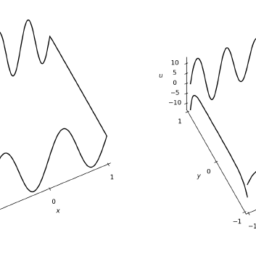
数学代写| Chebyshev differentiation matrix 数值分析代考
数值分析代写
Let $\left{x_{i}\right}_{i=0}^{n}$ denote the Chebyshev points $x_{i}=\cos (i \pi / n)$.
Theorem $\mathbf{0 . 4}$.
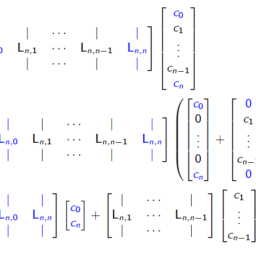
For $n \geq 1$ the Chebyshev differentiation matrix $D_{n} \in \mathbb{R}^{(n+1) \times(n+1)}$ is given by (indexing starts from 0)
$$
\begin{aligned}
{\left[\mathrm{D}{n}\right]{00} } &=\frac{2 n^{2}+1}{6} \
{\left[\mathrm{D}{n}\right]{n n} } &=-\frac{2 n^{2}+1}{6} \
{\left[\mathrm{D}{n}\right]{j j} } &=-\frac{x_{j}}{2\left(1-x_{j}^{2}\right)}, \quad j=1, \ldots, n-1 \
{\left[\mathrm{D}{n}\right]{i j} } &=\frac{c_{i}}{c_{j}} \frac{(-1)^{i+j}}{\left(x_{i}-x_{j}\right)}, \quad i \neq j, \quad i, j=0, \ldots, n
\end{aligned}
$$
where $c_{i}= \begin{cases}2 & i=0, n, \ 1 & \text { otherwise }\end{cases}$
Chebyshev differentiation matrix
- By the property of $\log$,
$$
\log L_{j}(x)=\left(\sum_{i=0 \atop i \neq j}^{n} \log \left(x-x_{i}\right)\right)-\log \left(\prod_{i=0 \atop i \neq j}^{n}\left(x_{j}-x_{i}\right)\right)
$$ - Thus, we can take the derivative of $\log L_{j}$,
$$
\left(\log L_{j}(x)\right)^{\prime}=\frac{L_{j}^{\prime}(x)}{L_{j}(x)}=\left(\sum_{i=0 \atop i \neq j}^{n} \log \left(x-x_{i}\right)\right)^{\prime}=\sum_{i=0 \atop i \neq j}^{n} \frac{1}{x-x_{i}}
$$ - That is,
$$
L_{j}^{\prime}(x)=L_{j}(x) \sum_{i=0 \atop i \neq j}^{n} \frac{1}{x-x_{i}}
$$ - Evaluating $L_{j}^{\prime}\left(x_{j}\right)$, we have
$$
L_{j}^{\prime}\left(x_{j}\right)=L_{j}\left(x_{j}\right) \sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i}}=\sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i}}
$$ - Evaluating $L_{j}^{\prime}\left(x_{i}\right)$ for $i \neq j$, we have
$$
\begin{aligned}
L_{j}^{\prime}\left(x_{i}\right) &=\lim {x \rightarrow x{i}} L_{j}(x) \sum_{k=0 \atop k \neq j}^{n} \frac{1}{x-x_{k}} \
&=\lim {x \rightarrow x{i}} \sum_{k=0 \atop k \neq j}^{n} \frac{L_{j}(x)}{x-x_{k}}=\lim {x \rightarrow x{i}} \frac{L_{j}(x)}{x-x_{i}} \
&=\lim {x \rightarrow x{i}} \prod_{k=0 \atop k \neq i, j}^{n \atop k \neq j}\left(x-x_{k}\right) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right) \
&=\prod_{k=0 \atop k \neq i, j}^{n}\left(x_{i}-x_{k}\right) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right)
\end{aligned}
$$- Evaluating $L_{j}^{\prime}\left(x_{j}\right)$, we have
$$
L_{j}^{\prime}\left(x_{j}\right)=L_{j}\left(x_{j}\right) \sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i}}=\sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i}}
$$ - Evaluating $L_{j}^{\prime}\left(x_{i}\right)$ for $i \neq j$, we have
$$
\begin{aligned}
L_{j}^{\prime}\left(x_{i}\right) &=\lim {x \rightarrow x{i}} L_{j}(x) \sum_{k=0 \atop k \neq j}^{n} \frac{1}{x-x_{k}} \
&=\lim {x \rightarrow x{i}} \sum_{k=0 \atop k \neq j}^{n} \frac{L_{j}(x)}{x-x_{k}}=\lim {x \rightarrow x{i}} \frac{L_{j}(x)}{x-x_{i}} \
&=\lim {x \rightarrow x{i}} \prod_{k=0 \atop k \neq i, j}^{n \atop k \neq j}\left(x-x_{k}\right) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right) \
&=\prod_{k=0 \atop k \neq i, j}^{n}\left(x_{i}-x_{k}\right) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right)
\end{aligned}
$$
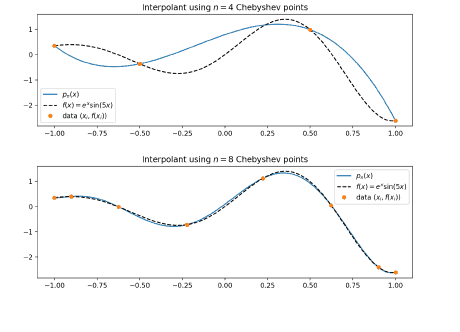
数值分析代考
令 $\left{x_{i}\right}_{i=0}^{n}$ 表示切比雪夫点 $x_{i}=\cos (i \pi / n)$。
定理 $\mathbf{0 . 4}$。
对于 $n \geq 1$,切比雪夫微分矩阵 $D_{n} \in \mathbb{R}^{(n+1) \times(n+1)}$ 由下式给出(索引从 0 开始)
$$
\开始{对齐}
{\left[\mathrm{D}{n}\right]{00} } &=\frac{2 n^{2}+1}{6} \
{\left[\mathrm{D}{n}\right]{n n} } &=-\frac{2 n^{2}+1}{6} \
{\left[\mathrm{D}{n}\right]{jj} } &=-\frac{x_{j}}{2\left(1-x_{j}^{2}\right) }, \quad j=1, \ldots, n-1 \
{\left[\mathrm{D}{n}\right]{ij} } &=\frac{c_{i}}{c_{j}} \frac{(-1)^{i+j} }{\left(x_{i}-x_{j}\right)}, \quad i \neq j, \quad i, j=0, \ldots, n
\end{对齐}
$$
其中 $c_{i}= \begin{cases}2 & i=0, n, \ 1 & \text { 否则 }\end{cases}$
切比雪夫微分矩阵
- 通过 $\log$ 的属性,
$$
\log L_{j}(x)=\left(\sum_{i=0 \atop i \neq j}^{n} \log \left(x-x_{i}\right)\right)-\log \left(\prod_{i=0 \atop i \neq j}^{n}\left(x_{j}-x_{i}\right)\right)
$$ - 因此,我们可以取 $\log L_{j}$ 的导数,
$$
\left(\log L_{j}(x)\right)^{\prime}=\frac{L_{j}^{\prime}(x)}{L_{j}(x)}=\left( \sum_{i=0 \atop i \neq j}^{n} \log \left(x-x_{i}\right)\right)^{\prime}=\sum_{i=0 \atop i \ neq j}^{n} \frac{1}{x-x_{i}}
$$ - 那是,
$$
L_{j}^{\prime}(x)=L_{j}(x) \sum_{i=0 \atop i \neq j}^{n} \frac{1}{x-x_{i}}
$$ - 评估 $L_{j}^{\prime}\left(x_{j}\right)$,我们有
$$
L_{j}^{\prime}\left(x_{j}\right)=L_{j}\left(x_{j}\right) \sum_{i=0 \atop i \neq j}^{n } \frac{1}{x_{j}-x_{i}}=\sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i} }
$$ - 为 $i \neq j$ 计算 $L_{j}^{\prime}\left(x_{i}\right)$,我们有
$$
\开始{对齐}
L_{j}^{\prime}\left(x_{i}\right) &=\lim {x \rightarrow x{i}} L_{j}(x) \sum_{k=0 \atop k \ neq j}^{n} \frac{1}{x-x_{k}} \
&=\lim {x \rightarrow x{i}} \sum_{k=0 \atop k \neq j}^{n} \frac{L_{j}(x)}{x-x_{k}} =\lim {x \rightarrow x{i}} \frac{L_{j}(x)}{x-x_{i}} \
&=\lim {x \rightarrow x{i}} \prod_{k=0 \atop k \neq i, j}^{n \atop k \neq j}\left(x-x_{k}\right ) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right) \
&=\prod_{k=0 \atop k \neq i, j}^{n}\left(x_{i}-x_{k}\right) / \prod_{k=0 \atop k \neq j} ^{n}\left(x_{j}-x_{k}\right)
\end{对齐}
$$- 计算 $L_{j}^{\prime}\left(x_{j}\right)$,我们有
$$
L_{j}^{\prime}\left(x_{j}\right)=L_{j}\left(x_{j}\right) \sum_{i=0 \atop i \neq j}^{n } \frac{1}{x_{j}-x_{i}}=\sum_{i=0 \atop i \neq j}^{n} \frac{1}{x_{j}-x_{i} }
$$ - 为 $i \neq j$ 计算 $L_{j}^{\prime}\left(x_{i}\right)$,我们有
$$
\开始{对齐}
L_{j}^{\prime}\left(x_{i}\right) &=\lim {x \rightarrow x{i}} L_{j}(x) \sum_{k=0 \atop k \ neq j}^{n} \frac{1}{x-x_{k}} \
&=\lim {x \rightarrow x{i}} \sum_{k=0 \atop k \neq j}^{n} \frac{L_{j}(x)}{x-x_{k}} =\lim {x \rightarrow x{i}} \frac{L_{j}(x)}{x-x_{i}} \
&=\lim {x \rightarrow x{i}} \prod_{k=0 \atop k \neq i, j}^{n \atop k \neq j}\left(x-x_{k}\right ) / \prod_{k=0 \atop k \neq j}^{n}\left(x_{j}-x_{k}\right) \
&=\prod_{k=0 \atop k \neq i, j}^{n}\left(x_{i}-x_{k}\right) / \prod_{k=0 \atop k \neq j} ^{n}\left(x_{j}-x_{k}\right)
\end{对齐}
$$

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程