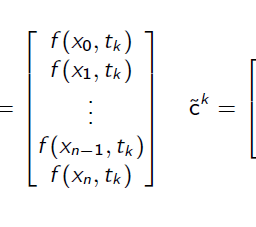数学代写| Chebyshev differentiation matrix 数值分析代考
数值分析代写
A simple boundary value problem
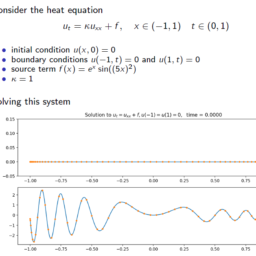
- Consider the Poisson problem
$$
u_{x x}(x)=f(x) \quad \text { for } x \in(-1,1), \quad u(-1)=0, \quad u(1)=0 .
$$
(here $\left.u_{x x}=u^{\prime \prime} .\right)$ The source term is given as $f(x)=e^{-x} \sin \left((5 x)^{2}\right)$ - The plan is to approximate $u$ by its interpolant $u_{n}$,
$$
u_{n}(x):=\sum_{i=0}^{n} c_{i} L_{i}(x)
$$ - The derivative of $u_{n}$ is approximated by
$$
u_{x, n}(x):=\sum_{i=0}^{n} u_{n}^{\prime}\left(x_{i}\right) L_{i}(x)
$$ - Similarly,
$$
u_{x x, n}(x):=\sum_{i=0}^{n} u_{n}^{\prime \prime}\left(x_{i}\right) L_{i}(x)
$$ - We can run the following code
1 import numpy as np
$\begin{aligned}&2 \&3\end{aligned} \quad x=n p \cdot \cos (n p \cdot$ linspace $(0, n p \cdot p i, N))$
$\begin{array}{ll}4 & \text { DN }=\text { df_mat }(x)\end{array}$
$\begin{array}{ll}5 & \mathrm{DN}=\mathrm{df}_{-} \text {mat }(\mathrm{x}) \ 6 & \mathrm{D} 2=\mathrm{DN} \cdot \operatorname{dot}(\mathrm{DN})\end{array}$
$\begin{array}{ll}7 & \mathrm{c}=\mathrm{np} \cdot \mathrm{zeros}((\mathrm{N}))\end{array}$
$f=f \operatorname{unc}(x)$
tD2 $=$ D2 $[1:(N-1), 1:(N-1)]$
$t f=f[1:(N-1)]$
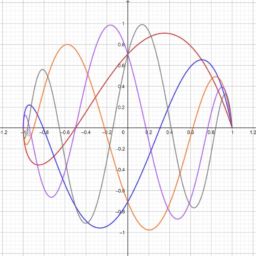
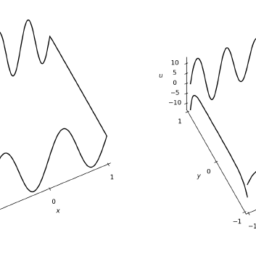
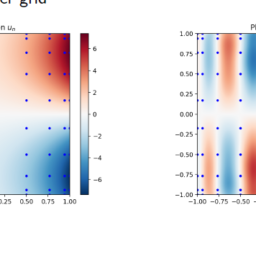
$c[1:(N-1)]=n p \cdot l i n a l g \cdot s o l v e(t D 2, t f)$ - Plotting the resulting solution using a finer grid
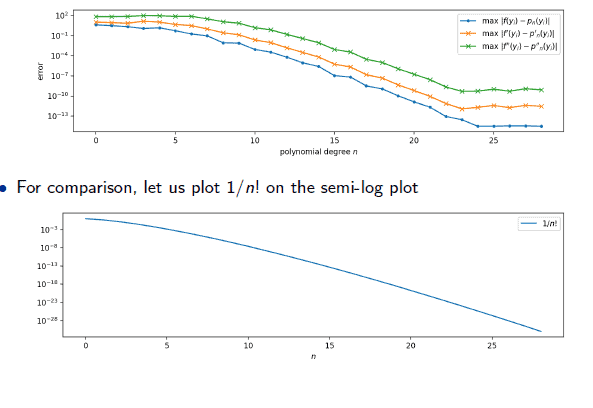
数值分析代考
一个简单的边值问题
- 考虑泊松问题
$$
u_{x x}(x)=f(x) \quad \text { for } x \in(-1,1), \quad u(-1)=0, \quad u(1)=0 。
$$
(这里 $\left.u_{xx}=u^{\prime \prime} .\right)$ 源项给出为 $f(x)=e^{-x} \sin \left((5 x )^{2}\右)$ - 该计划是通过其插值 $u_{n}$ 来近似 $u$,
$$
u_{n}(x):=\sum_{i=0}^{n} c_{i} L_{i}(x)
$$ - $u_{n}$ 的导数近似为
$$
u_{x, n}(x):=\sum_{i=0}^{n} u_{n}^{\prime}\left(x_{i}\right) L_{i}(x)
$$ - 相似地,
$$
u_{x x, n}(x):=\sum_{i=0}^{n} u_{n}^{\prime \prime}\left(x_{i}\right) L_{i}(x)
$$ - 我们可以运行以下代码
1 将 numpy 导入为 np
$\begin{对齐}&2 \&3\end{对齐} \quad x=n p \cdot \cos (n p \cdot$ linspace $(0, n p \cdot p i, N))$
$\begin{array}{ll}4 & \text { DN }=\text { df_mat }(x)\end{array}$
$\begin{数组}{ll}5 & \mathrm{DN}=\mathrm{df}_{-} \text {mat }(\mathrm{x}) \ 6 & \mathrm{D} 2=\ mathrm{DN} \cdot \operatorname{dot}(\mathrm{DN})\end{array}$
$\begin{array}{ll}7 & \mathrm{c}=\mathrm{np} \cdot \mathrm{zeros}((\mathrm{N}))\end{array}$
$f=f \operatorname{unc}(x)$
tD2 $=$ D2 $[1:(N-1), 1:(N-1)]$
$t f=f[1:(N-1)]$
$c[1:(N-1)]=n p \cdot l i n a l g \cdot s o l v e(t D 2, t f)$ - 使用更精细的网格绘制得到的解决方案

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程