数学代写|Differentiation in matrix form 数值分析代写
数值分析代写
The application of differentiation matrix in the $x$-direction can be written for the vector $c \in \mathbb{R}^{n^{2}}$ as the product
$$\mathrm{D}{n}^{(x)}:=\mathrm{I}{n} \otimes \mathrm{D}_{n}$$
where $\otimes$ denotes the Kronecker delta
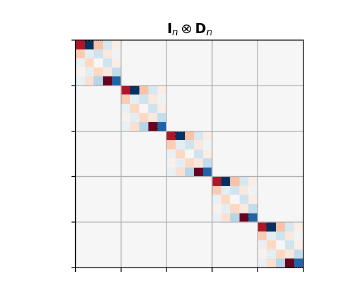
This matrix is simply multiple copies of $\mathrm{D}_{n}$. Visualizing the entries,
In numpy, this matrix can be computed
$$\mathrm{Dxn}=\mathrm{np} \cdot \mathrm{kron}(\mathrm{In}, \mathrm{Dn})$$
As we briefly discussed last lecture, higher order derivatives can be taken as
$$\left(\mathrm{D}{n}^{(y)}\right)^{k}:=\left(\mathrm{D}{n}\right)^{k} \otimes \mathrm{I}{n} $$ and similarly, $$ \left(\mathrm{D}{n}^{(x)}\right)^{k}:=\mathrm{I}{n} \otimes\left(\mathrm{D}{n}\right)^{k}$$
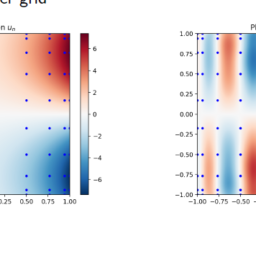
For example, the Laplacian of $u_{n}(x, y)=\sum_{i, j=0}^{n} c_{j, i} L_{i}(x) L_{j}(y)$,
$$u_{x x, n}+u_{y y, n}$$
can be computed by
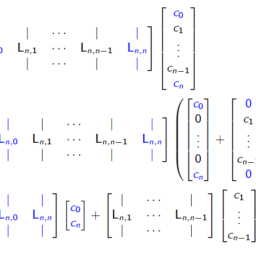
$$
\left[L_{n}^{(x)}+L_{n}^{(y)}\right] \mathrm{c} \quad L_{n}^{(x)}:=\left(D_{n}^{(x)}\right)^{2} \quad L_{n}^{(y)}:=\left(D_{n}^{(y)}\right)^{2}
$$
where $c \in \mathbb{R}^{(n+1)^{2}}$ is the flattened version of $c_{j, i}$.
We wish to impose the equations arising in the differential equation for the Chebyshev points in the interior only (\bullet)
Assign boundary values for the Chebyshev points on the boundary $(x)$.
$$
数值分析代考
微分矩阵在$x$ 方向的应用可以写成向量$c \in \mathbb{R}^{n^{2}}$ 为乘积
$$
\mathrm{D}{n}^{(x)}:=\mathrm{I}{n} \otimes \mathrm{D}_{n}
$$
其中$\otimes$ 表示克罗内克三角洲
- 这个矩阵只是 $\mathrm{D}_{n}$ 的多个副本。可视化条目,
- 在numpy中,可以计算这个矩阵
$$
\mathrm{Dxn}=\mathrm{np} \cdot \mathrm{kron}(\mathrm{In}, \mathrm{Dn})
$$ - 正如我们在上一课中简要讨论过的,高阶导数可以被视为
$$
\left(\mathrm{D}{n}^{(y)}\right)^{k}:=\left(\mathrm{D}{n}\right)^{k} \otimes \mathrm {在}
$$
同样,
$$
\left(\mathrm{D}{n}^{(x)}\right)^{k}:=\mathrm{I}{n} \otimes\left(\mathrm{D}_{n} \对)^{k}
$$ - 例如,$u_{n}(x, y)=\sum_{i, j=0}^{n} c_{j, i} L_{i}(x) L_{j}(y )$
$$
u_{x x, n}+u_{y y, n}
$$
可以通过计算
$$
\left[L_{n}^{(x)}+L_{n}^{(y)}\right] \mathrm{c} \quad L_{n}^{(x)}:=\left(D_ {n}^{(x)}\right)^{2} \quad L_{n}^{(y)}:=\left(D_{n}^{(y)}\right)^{2}
$$
其中 $c \in \mathbb{R}^{(n+1)^{2}}$ 是 $c_{j, i}$ 的扁平化版本。 - 我们希望仅将微分方程中出现的方程应用于内部的切比雪夫点 (\bullet)
- 为边界 $(x)$ 上的切比雪夫点分配边界值。
$$

数学代写|Differentiation in matrix form 数值分析代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程