数学代写代考| Finite-State Machines 离散数学代写 - 代考代写：100%准时可靠您的作业代写专家

The neurophysiologists Warren McCulloch and Walter Pitts published early work on finite-state automata in 1943 . They were interested in modelling the thought process for humans and machines. Moore and Mealy developed this work further in the mid-1950s, and their finite-state machines are referred to as the ‘Mealy machine’ and the ‘Moore machine’. The Mealy machine determines its outputs through the current state and the input, whereas the output of Moore’s machine is based upon the current state alone.

Definition 7.1 (Finite-State Machine) A finite-state machine (FSM) is an abstract mathematical machine that consists of a finite number of states. It includes a start state $q_{0}$ in which the machine is in initially; a finite set of states $Q$; an input alphabet $\Sigma ;$ a state transition function $\delta$ and a set of final accepting states $\mathrm{F}$ (where $F \subseteq Q$ ).
The state transition function $\delta$ takes the current state and an input symbol, and returns the next state. That is, the transition function is of the form:
$$
\delta: \mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}
$$
The transition function provides rules that define the action of the machine for each input symbol, and its definition may be extended to provide output as well as a transition of the state. State diagrams are used to represent finite-state machines, and each state accepts a finite number of inputs. A finite-state machine (Fig. 7.1) may be deterministic or non-deterministic, and a deterministic machine changes to exactly machine may have a choice of states to move for a particular input symbol.
Finite-state automata can compute only very primitive functions, and so they are not adequate as a model for computing. There are more powerful automata such as the Turing machine that is essentially a finite automaton with a potentially infinite storage (memory). Anything that is computable by a Turing machine.

A finite-state machine can model a system that has a finite number of states, and a finite number of inputs/events that can trigger transitions between states. The behaviour of the system at a point in time is determined from the current state and input, with behaviour defined for the possible input to that state. The system starts in a particular initial state.

A finite-state machine (also known as finite-state automata) is a quintuple $(\Sigma, Q,$, $\left.\delta, q_{0}, F\right) .$ The alphabet of the FSM is given by $\Sigma$; the set of states is given by $Q$; the transition function is defined by $\delta: Q \times \Sigma \rightarrow Q$; the initial state is given by $q_{0}$ and the set of accepting states is given by $F$ where $F$ is a subset of $Q .$ A string is given by a sequence of alphabet symbols: i.e. $s \in \Sigma^{}$, and the transition function $\delta$ can be extended to $\delta^{}: Q \times \Sigma^{} \rightarrow Q$ $\overline{{ }^{1} \text { The transition function may be undefined for a particular input symbol and state. }}$ $7.2$ Finite-State Machines 123 Fig. 7.1 Finite-state machine Fig. $7.2$ Deterministic FSM \begin{tabular}{l|l|l|l|l|} \hline Table table & State transition & 0 & 1 \ \hline \end{tabular} A string $s \in \Sigma^{}$ is accepted by the finite-state machine if $\delta^{*}\left(q_{0}, s\right)=q_{f}$ where $q_{f} \in F$, and the set of all strings accepted by a finite-state machine is the language generated by the machine. A finite-state machine is termed deterministic (Fig. 7.2) if the transition function $\delta$ is a function, ${ }^{2}$ and otherwise (where it is a relation) it is said to be non-deterministic. A non-deterministic automata is one for which the next state is not uniquely determined from the present state and input symbol, and the transition may be to a set of states rather than a single state.

For the example above the input alphabet is given by $\Sigma={0,1}$; the set of states by ${\mathrm{A}, \mathrm{B}, \mathrm{C}}$; the start state by $\mathrm{A}$; the final state by ${\mathrm{C}}$ and the transition function is given by the state transition table below (Table 7.1). The language accepted by the automata is the set of all binary strings that end with a one that contain exactly two ones.

A non-deterministic automaton (NFA) or non-deterministic finite-state machine is a finite-state machine where from each state of the machine and any given input, the machine may jump to several possible next states. However, a non-deterministic automaton (Fig. 7.3) is equivalent to a deterministic automaton, in that they both recognize the same formal language (i.e. regular languages as defined in Chomsky’s
${ }^{2}$ It may be a total or a partial function (as discussed in Chap. 2).
124
7 Automata Theory
$a, b$
Fig. $7.3$ Non-deterministic finite-state machine
classification). Further, for any non-deterministic automaton, it is possible to construct the equivalent deterministic automaton using power set construction.

NFAs were introduced by Scott and Rabin in 1959 , and a NFA is defined formally as a 5-tuple $\left(\mathrm{Q}, \Sigma, \delta, q_{\mathrm{o}}, F\right)$ as in the definition of a deterministic automaton, and the only difference is in the transition function $\delta$.
$$
\delta: Q \times \Sigma \rightarrow \mathbb{P} Q
$$
The non-deterministic finite-state machine $M_{1}=\left(Q, \Sigma, \delta, q_{o}, F\right)$ may be converted to the equivalent deterministic machine $M_{2}=\left(Q \prime, \Sigma, \delta \prime, q \prime_{o}, F \prime\right)$ where
$$
\begin{aligned}
Q^{\prime} &=\mathbb{P} Q(\text { the set of all subsets of } Q) \
q_{o}^{\prime} &=\left{q_{o}\right} \
F^{\prime} &=\left{q \in Q^{\prime} \text { and } q \cap F \neq \emptyset\right} \
\delta^{\prime}(q, \sigma) &=\cup_{p \in q} \delta(p, \sigma) \text { for each state } q \in Q^{\prime} \text { and } \sigma \in \Sigma .
\end{aligned}
$$
The set of strings (or language) accepted by an automaton $M$ is denoted $L(M)$. That is, $L(M)=\left{s: \mid \delta^{}\left(q_{0}, s\right)=q_{f}\right.$ for some $\left.q_{f} \in F\right} .$ A language is termed regular if it is accepted by some finite-state machine. Regular sets are closed under union, intersection, concatenation, complement and transitive closure. That is, for regular sets $A, B \subseteq \Sigma^{}$ then

$\mathrm{A} \cup \mathrm{B}$ and $\mathrm{A} \cap \mathrm{B}$ are regular.
$\Sigma^{*} \backslash$ A (i.e. $A^{c}$ ) is regular.
$\mathrm{AB}$ and $\mathrm{A}^{*}$ is regular.
The proof of these properties is demonstrated by constructing finite-state machines to accept these languages. For example, the proof that $A \cap B$ is regular is to construct a machine $\mathrm{M}{\mathrm{A} \cap \mathrm{B}}$ that mimics the execution of $\mathrm{M}{\mathrm{A}}$ and $\mathrm{M}{\mathrm{B}}$ and is in a final state if and only if both $\mathrm{M}{\mathrm{A}}$ and $\mathrm{M}_{\mathrm{B}}$ are in a final state. Finite-state machines are useful in designing systems that process sequences of data.

神经生理学家 Warren McCulloch 和 Walter Pitts 于 1943 年发表了关于有限状态自动机的早期工作。他们对模拟人类和机器的思维过程很感兴趣。 Moore 和 Mealy 在 1950 年代中期进一步发展了这项工作，他们的有限状态机被称为“Mealy 机器”和“Moore 机器”。 Mealy 机器通过当前状态和输入确定其输出，而 Moore 机器的输出仅基于当前状态。

定义 7.1（有限状态机）有限状态机 (FSM) 是一种抽象的数学机器，由有限数量的状态组成。它包括机器最初处于的起始状态$q_{0}$；有限状态集$Q$；一个输入字母 $\Sigma ;$ 一个状态转换函数 $\delta$ 和一组最终接受状态 $\mathrm{F}$ （其中 $F \subseteq Q$ ）。
状态转换函数 $\delta$ 接受当前状态和输入符号，并返回下一个状态。也就是说，转移函数的形式为：
$$
\delta: \mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}
$$
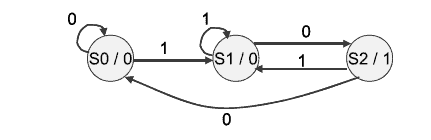
转换函数提供了为每个输入符号定义机器动作的规则，并且可以扩展其定义以提供输出以及状态转换。状态图用于表示有限状态机，每个状态接受有限数量的输入。有限状态机（图 7.1）可能是确定性的或非确定性的，而确定性机器更改为精确机器可能具有针对特定输入符号移动的状态选择。
有限状态自动机只能计算非常原始的函数，因此它们不足以作为计算模型。还有更强大的自动机，例如图灵机，它本质上是一个具有潜在无限存储（内存）的有限自动机。任何可由图灵机计算的东西。

有限状态机可以对具有有限数量的状态以及可以触发状态之间转换的有限数量的输入/事件的系统进行建模。系统在某个时间点的行为由当前状态和输入确定，并为该状态的可能输入定义行为。系统以特定的初始状态启动。

有限状态机（也称为有限状态自动机）是五元组 $(\Sigma, Q,$, $\left.\delta, q_{0}, F\right) .$ FSM 的字母表是由 $\Sigma$ 给出；状态集由 $Q$ 给出；转换函数由 $\delta 定义：Q \times \Sigma \rightarrow Q$；初始状态由 $q_{0}$ 给出，接受状态集由 $F$ 给出，其中 $F$ 是 $Q 的子集。$ 字符串由一系列字母符号给出：即 $s \in \Sigma^{}$，转移函数$\delta$可以扩展为$\delta^{}：Q \times \Sigma^{} \rightarrow Q$ $\overline{{ }^{1} \text { 对于特定的输入符号和状态，转换函数可能是未定义的。 }}$ $7.2$ 有限状态机 123 图 7.1 有限状态机图 $7.2$ 确定性 FSM \begin{表格}{l|l|l|l|l|} \hline 表表 & 状态转换 & 0 & 1 \ \hline \end{表格} 如果 $\delta^{}\left(q_{0}, s\right)=q_{f}$ where $q_ 则字符串 $s \in \Sigma^{*}$ 被有限状态机接受{f} \in F$，有限状态机接受的所有字符串的集合就是机器生成的语言。如果转移函数 $\delta$ 是一个函数 ${ }^{2}$ ，则一个有限状态机被称为确定性的（图 7.2），否则（如果它是一个关系）它被称为是非确定性的.非确定性自动机是下一个状态不是从当前状态和输入符号唯一确定的自动机，并且转换可能是到一组状态而不是单个状态。

对于上面的示例，输入字母表由 $\Sigma={0,1}$; ${\mathrm{A}, \mathrm{B}, \mathrm{C}}$ 的状态集； $\mathrm{A}$ 的起始状态；最终状态由 ${\mathrm{C}}$ 给出，转换函数由下面的状态转换表给出（表 7.1）。自动机接受的语言是所有以一个结尾的二进制字符串的集合，该字符串恰好包含两个字符串。

非确定性自动机 (NFA) 或非确定性有限状态机是一种有限状态机，其中从机器的每个状态和任何给定的输入，机器可以跳转到几个可能的下一个状态。然而，非确定性自动机（图 7.3）等价于确定性自动机，因为它们都识别相同的形式语言（即乔姆斯基定义的常规语言）
${ }^{2}$ 它可以是全函数或部分函数（如第 2 章所述）。
124
7 自动机理论
$a, b$
图 $7.3$ 非确定性有限状态机
分类）。此外，对于任何非确定性自动机，可以使用幂集构造来构造等价的确定性自动机。

NFA 由 Scott 和 Rabin 引入

在 1959 年，NFA 被正式定义为 5 元组 $\left(\mathrm{Q}, \Sigma, \delta, q_{\mathrm{o}}, F\right)$确定性自动机，唯一的区别在于转移函数$\delta$。
$$
\delta: Q \times \Sigma \rightarrow \mathbb{P} Q
$$
非确定性有限状态机 $M_{1}=\left(Q, \Sigma, \delta, q_{o}, F\right)$ 可以转换为等效的确定性机器 $M_{2}=\左（Q \prime，\Sigma，\delta \prime，q \prime_{o}，F \prime\right）$ 其中
$$
\开始{对齐}
Q^{\prime} &=\mathbb{P} Q(\text { } Q 的所有子集的集合) \
q_{o}^{\prime} &=\left{q_{o}\right} \
F^{\prime} &=\left{q \in Q^{\prime} \text { 和 } q \cap F \neq \emptyset\right} \
\delta^{\prime}(q, \sigma) &=\cup_{p \in q} \delta(p, \sigma) \text { 对于每个状态 } q \in Q^{\prime} \text {和 } \sigma \in \Sigma 。
\end{对齐}
$$
自动机 $M$ 接受的字符串（或语言）集合记为 $L(M)$。也就是说，对于某些 $\left，$L(M)=\left{s: \mid \delta^{}\left(q_{0}, s\right)=q_{f}\right.$。 q_{f} \in F\right} .$ 如果一种语言被某个有限状态机接受，则它被称为规则语言。正则集在并集、交集、连接、补集和传递闭包下是封闭的。也就是说，对于正则集 $A, B \subseteq \Sigma^{}$ 那么

$\mathrm{A} \cup \mathrm{B}$ 和 $\mathrm{A} \cap \mathrm{B}$ 是正则的。
$\Sigma^{*} \backslash$ A（即 $A^{c}$ ）是常规的。
$\mathrm{AB}$ 和 $\mathrm{A}^{*}$ 是正则的。
这些属性的证明是通过构造有限状态机来接受这些语言来证明的。例如，$A \cap B$ 是正则的证明是构造一个机器 $\mathrm{M}{\mathrm{A} \cap \mathrm{B}}$ 模仿 $\mathrm{ 的执行M}{\mathrm{A}}$ 和 $\mathrm{M}{\mathrm{B}}$ 当且仅当 $\mathrm{M}{\mathrm{A }}$ 和 $\mathrm{M}_{\mathrm{B}}$ 处于最终状态。有限状态机在设计处理数据序列的系统时很有用。

图论代考

排列是给定数量的对象的排列，一次取其中的一些或全部。组合是对多个对象的选择，其中选择的顺序并不重要。排列和组合是根据第 1 章中定义的阶乘函数定义的。 4.
计数原理
(a) 假设一个操作有 $m$ 个可能的结果，而第二个操作有 $n$ 个可能的结果，那么执行第一个操作后执行第二个操作时可能结果的总数是 $m \times n$ (Product Rule )。
(b) 假设一个操作有 $m$ 个可能的结果，而第二个操作有 $n$ 个可能的结果，那么第一个操作或第二个操作的可能结果总数由 $m+n$ 给出（求和规则） .
示例（计数原理 $(a)$ ）
假设掷骰子，然后掷硬币。有多少种不同的结果，它们是什么？
解决方案
掷骰子有六种可能的结果，$1,2,3,4,5$ 或 6，掷硬币有两种可能的结果，$\mathrm{H}$ 或 $\mathrm{ T}$。因此，结果的总数由乘积规则确定为 $6 \times 2=12$。结果由下式给出
$(1, \mathrm{H}),(2, \mathrm{H}),(3, \mathrm{H}),(4, \mathrm{H}),(5, \mathrm{H}) ,(6, \mathrm{H}),(1, \mathrm{~T}),(2, \mathrm{~T}),(3, \mathrm{~T}),(4, \mathrm{ ~T}),(5, \mathrm{~T}),(6, \mathrm{~T})$
示例（计数原理$(b)）$
假设掷骰子，如果数字是偶数，则掷硬币，如果是奇数，则第二次掷骰子。有多少种不同的结果？
解决方案
第一个实验涉及两个实验，涉及偶数和抛硬币。有 3 种可能的结果导致偶数和 2 种来自抛硬币的结果。因此，第一个实验有 $3 \times 2=6$ 的结果。

第二个实验涉及掷骰子和进一步掷骰子的奇数。掷骰子有 3 种可能的结果，导致奇数和 6 种结果。因此，第二个实验有 $3\times 6=18$ 的结果。
5.7 排列组合
97
最后，第一个实验有 6 个结果，第二个实验有 18 个结果，因此根据求和规则，总共有 $6+18=24$ 个结果。
鸽巢原理
鸽巢原则规定，如果将 $n$ 个项目放入 $m$ 个容器（其中 $n>m$），那么至少一个容器必须包含多个项目（图 5.1）。
示例（鸽洞原理）
(a) 假设有一组 367 人，那么必须至少有两个人的生日相同。

这很清楚，因为一年有 365 天（闰年有 366 天），所以一年最多有 366 个可能的生日。团体人数为 367 人，因此必须至少有两个人的生日相同。
(b) 假设有 102 名学生参加了一次考试（考试的结果是 0 到 100 之间的分数）。然后，至少有两名学生获得相同的分数。
这很清楚，因为测试有 101 种可能的结果（因为学生可能达到的分数介于 0 和 100 之间），并且班上有 102 名学生和 101 种可能的测试结果，那么必须至少有两名学生获得相同的分数。

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]