数学代写| Business Applications of Matrices 代考
离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法, 语言理论, 可计算性, 人工智能, 理论 数据库和软件的可靠性。 离散数学的重点是理论和应用,而不是为了数学本身而研究数学。 一切算法的基础都是离散数学一切加密的理论基础都是离散数学
编程时候很多奇怪的小技巧(特别是所有和位计算相关的东西)核心也是离散数学
其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
离散数学代写
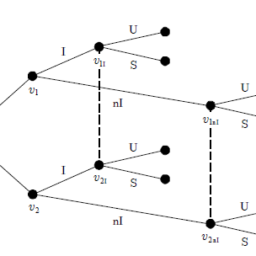
There are many applications of matrices in business and economics, and the field of linear programming often involves solving systems of linear equations. The organization structure of many organizations today is matrix orientated rather than the traditional functional structure with single managerial responsibility for a functional area in the organization. A matrix organization is one in which there is dual or multiple managerial accountability and responsibility, and there are generally two chains of command, with the first being along traditional functional lines and the second being along project or client Fig. 8.6.
That is, each person in a matrix organization is essentially reporting to two managers: their line manager for the functional area that they work in, and the project manager for the project that they are assigned to. The project is a temporary activity and so this reporting line ceases on project closure, whereas the functional line is more permanent (subject to the regular changes following company reorganizations as part of continuous improvement).
Another application of matrices in business is that of a decision matrix that allows an organization to make decisions objectively based on criteria. For example, the tool evaluation matrix in Table $8.1$ lists all of the requirements vertically that the tool is to satisfy, and the candidate tools that are to be evaluated and rated against each requirement are listed horizontally. Various rating schemes may be employed, and a simple numeric mechanism is employed in the example. The tool evaluation criteria are used to rate the effectiveness of each candidate tool, and
8.7 Business Applications of Matrices
145
\begin{tabular}{|l|l|l|l|l|l|l|}
\hline Table 8.1 Tool evaluation & & Tool 1 & Tool 2 & $\ldots$ & Tool $k$ \
\hline matrix & Requirement 1 & 8 & 7 & 9 \
\hline Requirement 2 & 4 & 6 & 8 \
\hline$\ldots$ & $\ldots$ & & & \
\hline & Requirement $n$ & 3 & 6 & & 8 \
\hline Total & 35 & 38 & $\ldots$ & 45 \
\hline
\end{tabular}
indicate the extent to which the tool satisfies the defined requirements. The chosen tool in this example is Tool $k$ as it is the most highly rated of the evaluated tools.
There are many applications of matrices in the computing field including in cryptography, coding theory and graph theory. For more detailed information on matrix theory see [2].、
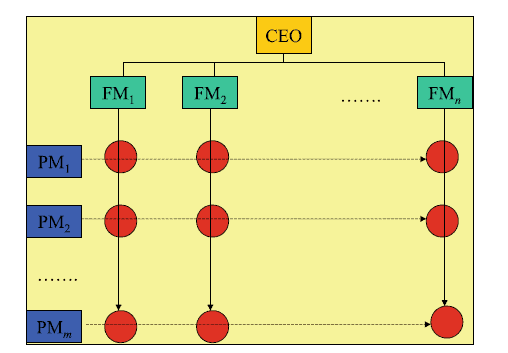
矩阵在商业和经济学中有很多应用,线性规划领域经常涉及求解线性方程组。当今许多组织的组织结构是矩阵导向的,而不是传统的职能结构,对组织中的一个职能领域具有单一的管理责任。矩阵式组织是一种具有双重或多重管理责任和责任的组织,通常有两条指挥链,第一条沿着传统的职能线,第二条沿着项目或客户图 8.6。
也就是说,矩阵式组织中的每个人基本上都向两个经理汇报:他们工作的职能领域的直线经理,以及他们被分配到的项目的项目经理。该项目是一项临时活动,因此该报告线在项目结束时停止,而职能线则更为永久(受公司重组后的定期更改作为持续改进的一部分)。
矩阵在商业中的另一个应用是决策矩阵,它允许组织根据标准客观地做出决策。例如,表 $8.1$ 中的工具评估矩阵垂直列出了该工具要满足的所有要求,而要针对每个要求进行评估和评级的候选工具则水平列出。可以采用各种评级方案,并且在示例中采用了简单的数字机制。工具评估标准用于评估每个候选工具的有效性,以及
8.7 矩阵的商业应用
145
\begin{表格}{|l|l|l|l|l|l|l|}
\hline 表 8.1 工具评估 & & 工具 1 & 工具 2 & $\ldots$ & 工具 $k$ \
\hline 矩阵 & 要求 1 & 8 & 7 & 9 \
\hline 要求 2 & 4 & 6 & 8 \
\hline$\ldots$ & $\ldots$ & & & \
\hline & 需求 $n$ & 3 & 6 & & 8 \
\hline 总计 & 35 & 38 & $\ldots$ & 45 \
\hline
\end{表格}
指出工具满足定义要求的程度。本例中选择的工具是 Tool $k$,因为它是评估工具中评价最高的。
矩阵在计算领域有很多应用,包括密码学、编码理论和图论。有关矩阵理论的更多详细信息,请参见 [2]。
图论代考
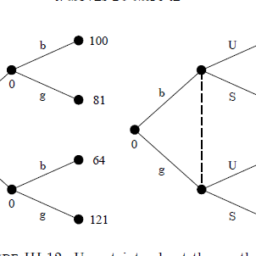
自然数 $\mathbb{N}$ 由数字 $\{1,2,3, \ldots\}$ 组成。整数 $\mathbb{Z}$ 由 $\{\ldots-2,-1,0,1,2, \ldots\}$ 组成。有理数 $\mathbb{Q}$ 由 $\left\{{ }^{p} /_{q}\right.$ 形式的所有数字组成,其中 $p$ 和 $q$ 是整数,$ \left.q \neq 0\right\}$。实数 $\mathbb{R}$ 被定义为有理数收敛序列的集合,它们是有理数的超集。它们包含有理数和无理数。复数 $\mathbb{C}$ 由 $\{a+bi$ 形式的所有数字组成,其中 $a, b \in \mathbb{R}$ 和 $i=\sqrt{-} 1\}美元。 毕达哥拉斯三元组(图 3.2)是满足毕达哥拉斯方程 $x^{2}+y^{2}=z^{2}$ 的三个整数的组合。有无数个这样的三元组,这种三元组的一个例子是 $3,4,5$,因为 $3^{2}+4^{2}=5^{2}$。 毕达哥拉斯学派发现了音乐和数字之间的数学关系,他们的哲学是数字隐藏在从音乐到科学和自然的一切事物中。这导致了他们的哲学,即“一切都是数字”。

数学代写| DISCRETE MATHEMATICS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
抽象代数代考
抽象代数就是一门概念繁杂的学科,我们最重要的一点我想并不是掌握多少例子。即便是数学工作者也不会刻意记住Jacobson环、正则环这类东西,重要的是你要知道这门学科的基本工具和基本手法,对概念理解了没有,而这一点不需要用例子来验证,只需要看看你的理解和后续概念是否相容即可。
矩阵论代考matrix theory
数学,矩阵理论是一门研究矩阵在数学上的应用的科目。矩阵理论本来是线性代数的一个小分支,但其后由于陆续在图论、代数、组合数学和统计上得到应用,渐渐发展成为一门独立的学科。
密码学代考
密码学是研究编制密码和破译密码的技术科学。 研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。 电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。
- Cryptosystem
- A system that describes how to encrypt or decrypt messages
- Plaintext
- Message in its original form
- Ciphertext
- Message in its encrypted form
- Cryptographer
- Invents encryption algorithms
- Cryptanalyst
- Breaks encryption algorithms or implementations
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。