MY-ASSIGNMENTEXPERT™可以为您提供 handbook MTH3330 Operations research运筹学的代写代考和辅导服务!
这是莫纳什大学 运筹学的代写成功案例。
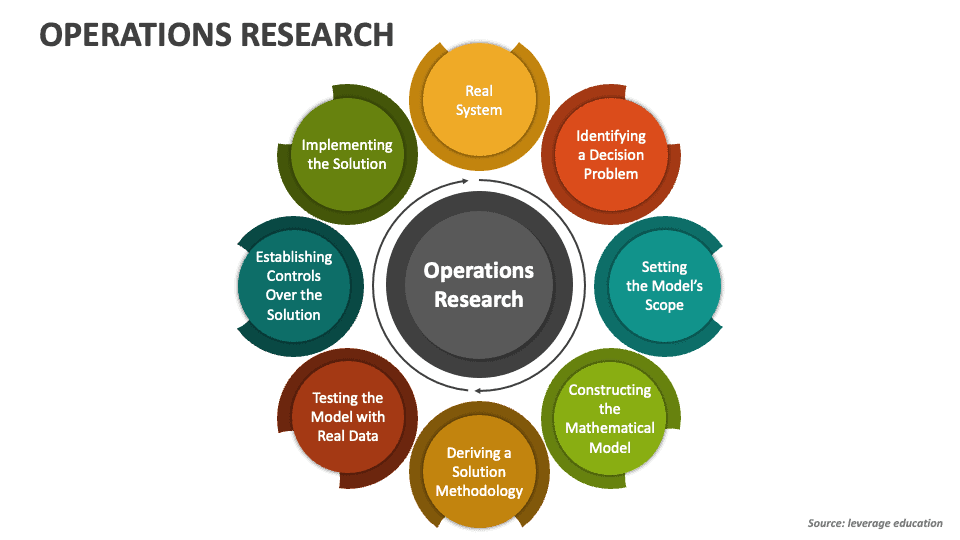
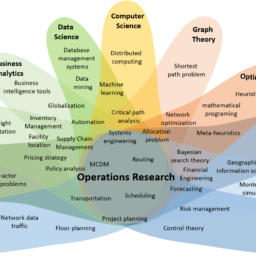
MATH3330课程简介
This unit introduces some of the fundamental methods from operations research and computational mathematics for continuous optimisation problems. A range of such optimisation problems arise in economics, engineering, finance, business, data science and many other application areas. You will receive an introduction to the mathematical theory of continuous optimisation with a focus on linear programming methods and smooth non-linear programming. This will broadly include duality theory, the simplex method for linear programming, network optimisation and iterative methods for unconstrained nonlinear optimisation. You will also learn to implement the computational methods efficiently, how to test their implementations for accuracy and performance, and to interpret the results. You will work on optimisation models for applications in a variety of fields. Applications may include examples of supply chain optimisation, economic modelling (including shadow prices), product mix optimisation, portfolio optimisation, parameter estimation and machine learning.
Prerequisites
Enrolment Rule
keyboard_arrow_down
PREREQUISITE: You must have passed one of MTH2051 or MTH3051 or if you are enrolled in the Bachelor of Applied Data Science MTH2019 or both of (MTH2010 or MTH2015) and (MTH2021 or MTH2025) or if you are enrolled in the Honours of Econometrics, ETC2440 (this requires manual enrolment).
Alternatively you must be enrolled in the Master of Financial Mathematics, the Master of Mathematics, or receive special permission from the unit coordinator.
MTH3330 Operations research HELP(EXAM HELP, ONLINE TUTOR)
Since $T$ is exponential with mean $1 / 2$ hour,
$$
P(T>t)=e^{-2 t}, \quad t>0 .
$$
Hence,
(a)
$$
P(T>1 / 2)=e^{-2(1 / 2)}=e^{-1} \approx \frac{1}{2.71828} .
$$
(b) By the lack-of-memory property (see Section 5.2.2),
$$
P(T>12.5 \mid T>12)=P(T>1 / 2)=e^{-2(1 / 2)}=e^{-1} .
$$
The time you spend in the system, say $T$, is the sum of 6 IID (independent and identically distributed) exponential random variables, each with mean $1 / \mu$. Hence,
$$
E T=6 / \mu .
$$
The conditional distribution of $X$ given that $X>1$ is the same as the unconditional distribution of $1+X$. Hence
$$
E\left[X^2 \mid X>1\right]=E\left[(X+1)^2\right] ;
$$
i.e., (a) is correct.
(a) 0 , (b) one way: $\left(1 / 3^3=1 / 27\right.$, (c) $1 / 4$ because
$$
\begin{aligned}
(A \text { last to leave }) & =P(B \text { served before } A) \times P(C \text { served before } A \mid B \text { served before } A) \
& =(1 / 2) \times(1 / 2)=1 / 4
\end{aligned}
$$
Let $T$ be the lifetime of the radio. Then
$$
P(T>t \text { years })=e^{-0.1 t}, \quad t>0 .
$$
Hence, by the lack-of-memory property (again see Section 5.2.2),
$$
P(T>20 \mid T>10)=P(T>10)=e^{-0.1(10)}=e^{-1} .
$$

MY-ASSIGNMENTEXPERT™可以为您提供 HANDBOOK MATH3202 OPERATIONS RESEARCH运筹学的代写代考和辅导服务!