MY-ASSIGNMENTEXPERT™可以为您提供 soe.ucsc.edu STAT209 Generalized Linear Models广义线性模型的代写代考和辅导服务!
这是圣克鲁斯加利福尼亚大学 广义线性模型的代写成功案例。
STAT209课程简介
Theory, methods, and applications of generalized linear statistical models; review of linear models; binomial models for binary responses (including logistical regression and probit models); log-linear models for categorical data analysis; and Poisson models for count data. Case studies drawn from social, engineering, and life sciences.
Course description and background: This is a graduate-level course on the theory, methods and applications of Generalized Linear Models (GLMs). Emphasis will be placed on statistical modeling, building from standard normal linear models, extending to GLMs, and briefly covering more specialized topics. With regard to inference, prediction, and model assessment, we will study both likelihood and Bayesian methods. In particular, within the Bayesian modeling framework, we will discuss practically important hierarchical extensions of the standard GLM setting.
Prerequisites
Note that this is a course on methods for GLMs, rather than a course on using software for data analysis with GLMs. Students will be expected to be familiar with statistical software R, which will be used to illustrate the methods with data examples as part of the homework assignments (and exam). For data analysis problems involving Bayesian GLMs, you will be expected to write your own programs to fit Bayesian models using Markov chain Monte Carlo posterior simulation methods (R will suffice for this).
STAT209 Generalized Linear Models HELP(EXAM HELP, ONLINE TUTOR)
Let $X$ be a random variable with mean $\mu$ and variance $\sigma^2$ and let $g$ be a twice differentiable function. A Taylor expansion about $\mu$ gives
$$
g(X)-g(\mu)=(X-\mu) g^{\prime}(\mu)+\frac{1}{2} g^{\prime \prime}(\mu)(X-\mu)^2+\ldots
$$
ignoring all but the first term on the right hand side. Show that
$$
E[g(X)] \simeq g(\mu) \text { and } \operatorname{Var}[g(X)] \simeq \sigma^2\left[g^{\prime}(\mu)\right]^2
$$
Hence
(a) show that the variance-covariance matrix for the ML estimates $\widehat{\boldsymbol{\theta}}$ using the NewtonRaphson procedures is
$$
\operatorname{var}(\widehat{\boldsymbol{\theta}}) \simeq[\boldsymbol{I}(\widehat{\boldsymbol{\theta}})]^{-1}
$$
where $\boldsymbol{I}(\boldsymbol{\theta})$ is the informative matrix.
(b) find a function $g$ such that $\operatorname{Var}(g(X))$ is approximately constant when $X \sim \operatorname{Poisson}(\lambda)$.
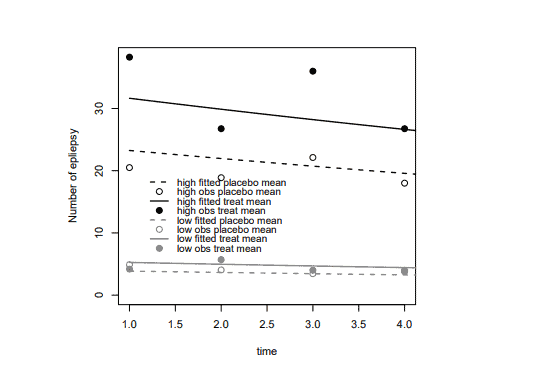
The following is the Leukaemia data which contain two samples: one sample of 21 patients was treated with 6-mercaptopurine and the other sample received a placebo. The time of remission in weeks is given below.
\begin{tabular}{lllrrr}
\multicolumn{2}{c}{ 6-MCP Group } & & \multicolumn{3}{r}{ Control Group } \
\hline $6^$ & 10 & 22 & 1 & 5 & 11 \ 6 & $11^$ & 23 & 1 & 5 & 12 \
6 & 13 & $25^$ & 2 & 8 & 12 \ 6 & 16 & $32^$ & 2 & 8 & 15 \
7 & $17^$ & $32^$ & 3 & 8 & 17 \
$9^$ & $19^$ & $34^$ & 4 & 8 & 22 \ $10^$ & $20^$ & $35^$ & 4 & 11 & 23 \
\hline
\end{tabular}
An asterisk denotes right-censored data.
Assume that the survival time $Y_i$ follows an exponential distribution, that is, $Y_i \sim \mathcal{E} x p\left(\lambda_i\right), i=$ $1, \ldots, 42$ where $f\left(y_i\right)=\lambda_i \exp \left(-\lambda_i y_i\right), E\left(Y_i\right)=\mu_i=\lambda_i^{-1}=\beta_0+\beta_1 x_i$ and $x_i=1$ if $Y_i$ comes
from the treatment group and 0 otherwise. The observed data is
$$
\left{\begin{array}{ll}
Y_i & \text { if } Y_i \text { is uncensored, } \
C_i & \text { if } Y_i \text { is censored at } C_i
\end{array} .\right.
$$
(a) Write down the log-likelihood function $\ell$ for the survival times $\boldsymbol{Y}=\left(Y_1, \ldots, Y_n\right)$ where $n=42$. Show that its first order derivative functions are
$$
\frac{\partial \ell}{\partial \beta_0}=\sum_{i=1}^n \frac{r_i}{\mu_i^2} \text { and } \frac{\partial \ell}{\partial \beta_1}=\sum_{i=1}^n \frac{x_i r_i}{\mu_i^2}
$$
and its second order derivative functions are
$$
\frac{\partial^2 \ell}{\partial \beta_0^2}=-\sum_{i=1}^n \frac{r_i+y_i}{\mu_i^3}, \quad \frac{\partial^2 \ell}{\partial \beta_1^2}=-\sum_{i=1}^n \frac{x_i^2\left(r_i+y_i\right)}{\mu_i^3} \text { and } \frac{\partial^2 \ell}{\partial \beta_0 \partial \beta_1}=-\sum_{i=1}^n \frac{x_i\left(r_i+y_i\right)}{\mu_i^3}
$$
where $r_i=y_i-\mu_i$.
(b) Show that the conditional expectation of $Y_i$ when it is censored at $C_i=c_i$ is
$$
E\left(Y_i \mid Y_i>c_i\right)=\int_{c_i}^{\infty} y_i \lambda_i e^{-\lambda_i\left(y_i-c_i\right)} d y_i=c_i+\beta_0+\beta_1 x_i
$$
where $\lambda_i e^{-\lambda_i\left(y_i-c_i\right)}$ is the pdf for the truncated exponential distribution.
(c) Using the result in (a) for the M-step and (b) for the E-step, estimate the model parameters using the EM algorithm and R. You should calculate the standard error estimates and AIC for each iteration.
Using the result in (a) for the M-step and (b) for the E-step, estimate the model parameters using the EM algorithm and R. You should calculate the standard error estimates and AIC for each iteration.
You may set the starting values for $\left(\beta_0, \beta_1\right)$ to be $(1,0.5)$ and use the following $\mathrm{R}$ codes.
$c y=c(6,6,6,6,7,9,10,10,11,13,16,17,19,20,22,23,25,32,32,34,35$,
$1,1,2,2,3,4,4,5,5,8,8,8,8,11,11,12,12,15,17,22,23)$
$w=c(0,1,1,1,1,0,0,1,0,1,1,0,0,0,1,1,0,0,0,0,0$
$1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)$
$x=c(r e p(1,21), \operatorname{rep}(0,21))$
$\mathrm{n}=\operatorname{length}(y)$
$p=2$
iterE=10
iterM=5
dim1=iterEiterM dim2=2p+3
dl=c(rep(0,p))
result=matrix(0, dim1, dim2)
theta=c(1,0.5)
se=c(0,0)
$c y=c(6,6,6,6,7,9,10,10,11,13,16,17,19,20,22,23,25,32,32,34,35$,
$1,1,2,2,3,4,4,5,5,8,8,8,8,11,11,12,12,15,17,22,23)$
$\mathrm{w}=\mathrm{c}(0,1,1,1,1,0,0,1,0,1,1,0,0,0,1,1,0,0,0,0,0$,
$1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)$
$x=c(\operatorname{rep}(1,21), \operatorname{rep}(0,21))$
$\mathrm{n}=$ length (y)
$p=2$
iter $E=10$
iterm $=5$
$\operatorname{dim} 1=i$ terE*iterM
$\operatorname{dim} 2=2 * p+3$
$d l=c(\operatorname{rep}(0, p))$
result=matrix $(0, \operatorname{dim} 1, \operatorname{dim} 2)$
theta $=c(1,0.5)$
$\mathrm{se}=\mathrm{c}(0,0)$
for (k in 1:iterE) ${\quad #$ E-step
$\ldots$
for (i in $1: i t e r M){\quad #$ M-step
$\ldots$
$\quad$ row $=(k-1) * i t e r M+i$
$\quad$ result $[$ row $]=c(k, i, \operatorname{theta}[1]$, se $[1], \operatorname{theta}[2]$, se $[2]$, aic $)$
}
}
colnames (result) $=c(” i E “$, “iM”, “beta0”, “se”, “beta1”, “se”, “aic”)
result
for ( $k$ in 1:iterE) ${\quad #$ E-step
…
for (i in $1:$ iterM) ${\quad #$ M-step
…
row $=(\mathrm{k}-1) *$ iterM $+\mathrm{i}$
result $[\operatorname{row}]=,c(k, i, \operatorname{theta}[1]$, se $[1]$, theta $[2]$, se $[2]$, aic $)$
}
}
colnames (result)=c(“iE”, “iM”, “beta0”, “se”, “beta1”, “se”, “aic”)
result
Hint: Because of the ordering of the censored data, it is more convenient to use a vector of indicators $w$ for the uncensored data. Then the vector of complete data is $\mathrm{y}=\mathrm{w} * \mathrm{cy}+(1-\mathrm{w}) * \mathrm{ey}$ where wcy gives a vector of observed cy and 0 for the censored data and (1-w)ey gives a vector of the conditional expectation ey in (b) for the censored data and 0 for the uncensored data.
Suppose the sample $t_i, i=1, \ldots, n$ follow a Rayleigh distribution $R(\sigma)$ with pdf
$$
f(t)=\frac{t}{\sigma^2} \exp \left(-\frac{t^2}{2 \sigma^2}\right), \quad t \geq 0
$$
and cdf
$$
F(t)=1-\exp \left(-\frac{t^2}{2 \sigma^2}\right) .
$$
Rayleigh distribution is shown to be a member of the exponential family with sufficient statistics $\sum_{i=1}^n t_i^2$ and
$$
E\left(T^2\right)=2 \sigma^2 \quad \text { and } \quad \operatorname{Var}\left(T^2\right)=4 \sigma^4
$$
(a) Use the inverse transform method to suggest a method to simulate Rayleigh distributed random variables.
(b) Show that $E\left(T^2\right)=2 \sigma^2$ by definition. Hence show that the mean and variance for Rayleigh distribution are respectively
$$
E(T)=\sqrt{\frac{\pi}{2}} \sigma \quad \text { and } \quad \operatorname{Var}(T)=\frac{4-\pi}{2} \sigma^2 .
$$
You may use the result: $\int_0^{\infty} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{t^2}{2 \sigma^2}\right) d t=\frac{1}{2}$.
(c) Show that the maximum likelihood estimator (MLE) of $\sigma$ is
$$
\hat{\sigma}=\sqrt{\frac{1}{2 n} \sum_{i=1}^n t_i^2}
$$
and find its standard error (se).
(d) By expressing $\operatorname{Var}(T)$ in terms of $\mu=E(T)$, show that the quasi-likelihood is
$$
Q(\mu, t)=\frac{\pi}{4-\pi}\left(-\frac{t}{\mu}+1-\ln \mu+\ln t\right) .
$$
Hence show that the maximum quasi-likelihood estimator (MQLE) $\tilde{\sigma}$ of $\sigma$ is a moment estimator and find its se. Explain why the MQLE of $\sigma$ is less efficient than the MLE.
(e) An estimator of $\sigma^2$ is defined to be $\widehat{\sigma^2}=(\hat{\sigma})^2$. Find the se of $\widehat{\sigma^2}$ using
(i) result of $(\mathrm{b})$,
(ii) Taylor expansion method: $\operatorname{Var}(g(\hat{\vartheta})) \simeq\left[g^{\prime}(\vartheta)\right]^2 \operatorname{Var}(\hat{\vartheta})$ where $\hat{\vartheta}$ is an estimator of $\vartheta$
which give the same se.

MY-ASSIGNMENTEXPERT™可以为您提供 SOE.UCSC.EDU STAT209 GENERALIZED LINEAR MODELS广义线性模型的代写代考和辅导服务