MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH3078 Partial Differential Equations偏微分方程的代写代考和辅导服务!
这是悉尼大学 偏微分方程的代写成功案例。
MATH3078课程简介
The aim of this unit is to introduce some fundamental concepts of the theory of partial differential equations (PDEs) arising in Physics, Chemistry, Biology and Mathematical Finance. The focus is mainly on linear equations but some important examples of nonlinear equations and related phenomena re introduced as well. After an introductory lecture, we proceed with first-order PDEs and the method of characteristics. Here, we also nonlinear transport equations and shock waves are discussed. Then the theory of the elliptic equations is presented with an emphasis on eigenvalue problems and their application to solve parabolic and hyperbolic initial boundary-value problems. The Maximum principle and Harnack’s inequality will be discussed and the theory of Green’s functions.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. demonstrating the ability to recognize different types of partial differential equations: “linear” or “nonlinear”, “order of the given equation”, “homogeneous” or “inhomogeneous”, and if it concerns 2nd-order equations, whether they are of “elliptic”, “parabolic”, or “hyperbolic” type
- LO2. demonstrating the conceptional understanding of how to apply different methods for solving different types of partial differential equations. Those methods include the use of classical ODE-concepts to solve PDEs
- LO3. understanding the definitions, main theorem, and corollaries of Green’s functions and Poisson kernel
- LO4. be fluent with “change of variable” into polar, cylindrical and spherically coordinates and to be able to compute partial derivatives in these coordinates
- LO5. develop an appreciation and strong working knowledge of the theory and application of elementary partial differential equations
- LO6. be fluent in using generalized Fourier transforms to solve parabolic and hyperbolic initial boundary value problems where the spatial variable might be of more than one variable
MATH3078 Partial Differential Equations HELP(EXAM HELP, ONLINE TUTOR)
This exercise is partly reprinted from [Strauss], §1.5, Exercise 5.
Consider the following PDE:
$$
\frac{\partial u}{\partial x}-y \frac{\partial u}{\partial y}=0
$$
of a function $u \equiv u(x, y)$ of two variables, together with the boundary condition $u(x, 0)=\varphi(x)$, where $\varphi(x)$ is a given function.
(1) What is the general solution to this equation (i.e. without considering boundary conditions) ?
(2) Show that, if $\varphi(x) \equiv x$, the considered system has no solution.
(3) Show that, if $\varphi(x) \equiv 1$, the considered system has an infinity of solutions.
This exercise is partly reprinted from [Strauss], 1.5 , Exercise 4.
Consider the Laplace problem with homogeneous Neumann boundary conditions, posed in a threedimensional domain $\Omega$ :
$$
\left{\begin{array}{c}
\Delta u=f \quad \text { in } \Omega \
\frac{\partial u}{\partial n}=0 \quad \text { on } \partial \Omega
\end{array},\right.
$$
where $f \equiv f(x, y, z)$ is a given source term, and $n$ is the unit normal vector to $\partial \Omega$, pointing outward $\Omega$.
(1) What can be added to any solution $u$ of the problem (1), so as to end up with another solution of this problem ? Conclude that there is no unicity of solutions to (1).
(2) Assume that there exists a solution $u$ to (1). By using the Green formula, show that necessarily, one then has:
$$
\int_{\Omega} f(x, y, z) d x d y d z=0 .
$$
Hence, does a solution to (1) always exist?
(3) Provide a physical interpretation to your answers to questions (1) and (2).
This exercise is partly reprinted from [Haberman], 1.4 , Exercise 3.
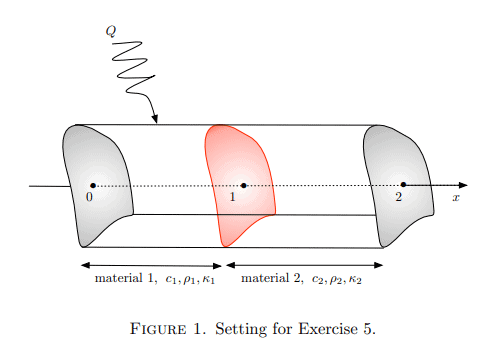
Consider a three dimensional rod oriented along the $x$-axis. The rod is very thin, and lies in the region $(0<x<2)$, so that we assume its temperature $u$ only depends on the time $t$ and on $x$. It is composed of two parts (see Figure 1):
- The first one, lying between $00,0<x<1$ the temperature in this part.
- The second one, lying between $10,1<x<2$ the temperature in this part.
The system is endowed with homogeneous Dirichlet boundary conditions:
$$
\forall t>0, u(t, 0)=0, v(t, 2)=0
$$
and the two materials are assumed to be in perfect thermal contact, i.e.:
$$
\forall t>0, u(t, 1)=v(t, 1), \kappa_1 \frac{\partial u}{\partial x}(t, 1)=\kappa_2 \frac{\partial v}{\partial x}(t, 1)
$$
(1) Provide a physical interpretation of the conditions (2). In the mechanical literature, such conditions are called transmission boundary conditions.
(2) Write the two PDEs satisfied by $u$ and $v$.
(3) We now assume that a steady state $(u(x), v(x))$ exists for this system. Find the expression of $u(x)$, $0<x<1$ and $v(x), 1<x<2$.
Find all solutions of the following system of equations using GaussJordan elimination. As usual, you need to show all work.
$$
\begin{aligned}
4 x_1+3 x_2+2 x_3-x_4 & =4 \
5 x_1+4 x_2+3 x_3-x_4 & =4 \
-2 x_1-2 x_2-x_3+2 x_4 & =-3 \
11 x_1+6 x_2+4 x_3+x_4 & =11
\end{aligned}
$$
Two $n \times m$ matrices in reduced row-echelon form are called of the same type if they contain the same number of leading l’s in the same positions. For example, $\left[\begin{array}{lll}1 & 2 & 0 \ 0 & 0 & 1\end{array}\right]$ and $\left[\begin{array}{lll}1 & 3 & 0 \ 0 & 0 & 1\end{array}\right]$ are of the same type. How many types of $2 \times 2$ matrices in reduced row-echelon form are there?

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH3078 PARTIAL DIFFERENTIAL EQUATIONS偏微分方程的代写代考和辅导服务!