如果你也在 怎样代写量子场论Quantum field theory 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。商量子场论Quantum field theory是经典场论、量子力学和狭义相对论结合的结果。最早成功的经典场论是由牛顿的万有引力定律产生的,尽管在他1687年的论文《Philosophiæ Naturalis Principia Mathematica》中完全没有场的概念。牛顿所描述的引力是一种 “远距离作用”–它对远处物体的影响是瞬间的,无论距离多远。
量子场论Quantum field theory通过博恩、海森堡和帕斯卡尔-乔丹在1925-1926年的工作,自由电磁场(没有与物质相互作用的电磁场)的量子理论通过经典量子化被开发出来,将电磁场视为一组量子谐波振荡器。 然而,由于排除了相互作用,这样的理论还不能对现实世界作出定量预测。
my-assignmentexpert™量子场论Quantum field theory代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的量子场论Quantum field theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此量子场论Quantum field theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在澳洲代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的澳洲代写服务。我们的专家在量子场论Quantum field theory代写方面经验极为丰富,各种量子场论Quantum field theory相关的作业也就用不着 说。
我们提供的量子场论Quantum field theory及其相关学科的代写,服务范围广, 其中包括但不限于:
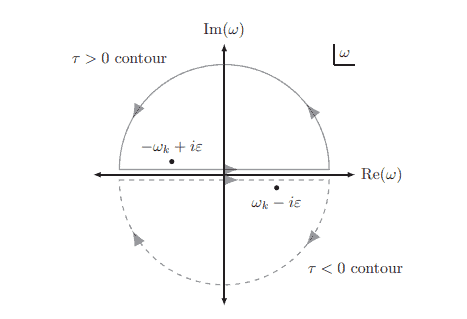
物理代考|量子场论代考Quantum field theory代考|The Feynman propagator
To recap, our immediate goal, as motived in Chapter 5 , is to calculate cross sections, which are determined by $S$-matrix elements. We now have an expression, the LSZ reduction formula, for $S$-matrix elements in terms of time-ordered products of fields. Next, we need to figure out how to compute those time-ordered products. As an example, we will now calculate a time-ordered product in the free theory. In Chapter 7 , we will derive a method for computing time-ordered products in interacting theories using perturbation theory.
We start with the free-field operator:
$$
\phi_0(x, t)=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{\sqrt{2 \omega_k}}\left(a_k e^{-i k x}+a_k^{\dagger} e^{i k x}\right),
$$
where $k_0=\omega_k=\sqrt{m^2+\vec{k}^2}$ and $a_k$ and $a_k^{\dagger}$ are time independent (all time dependence is in the phase). Then, using $|0\rangle$ instead of $|\Omega\rangle$ to denote the vacuum in the free theory,
$$
\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle=\int \frac{d^3 k_1}{(2 \pi)^3} \int \frac{d^3 k_2}{(2 \pi)^3} \frac{1}{\sqrt{2 \omega_{k_1}}} \frac{1}{\sqrt{2 \omega_{k_2}}}\left\langle 0\left|a_{k_1} a_{k_2}^{\dagger}\right| 0\right\rangle e^{i\left(k_2 x_2-k_1 x_1\right)} .
$$
The $\left\langle 0\left|a_{k_1} a_{k_2}^{\dagger}\right| 0\right\rangle$ gives $(2 \pi)^3 \delta^3\left(\vec{k}_1-\vec{k}_2\right)$ so that
$$
\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k} e^{i k\left(x_2-x_1\right)} .
$$
Now, we are interested in $\left\langle 0\left|T\left{\phi\left(x_1\right) \phi\left(x_2\right)\right}\right| 0\right\rangle$. Recalling that time ordering puts the later field on the left, we get
$$
\begin{aligned}
\left\langle 0\left|T\left{\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right}\right| 0\right\rangle & =\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle \theta\left(t_1-t_2\right)+\left\langle 0\left|\phi_0\left(x_2\right) \phi_0\left(x_1\right)\right| 0\right\rangle \theta\left(t_2-t_1\right) \
& =\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k}\left[e^{i k\left(x_2-x_1\right)} \theta\left(t_1-t_2\right)+e^{i k\left(x_1-x_2\right)} \theta\left(t_2-t_1\right)\right] \
& =\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k}\left[e^{i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)} e^{-i \omega_k \tau} \theta(\tau)+e^{-i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)} e^{i \omega_k \tau} \theta(-\tau)\right],
\end{aligned}
$$
where $\tau=t_1-t_2$. Taking $k \rightarrow-k$ in the first term leaves the volume integral $\int d^3 k$ invariant and gives
$$
\left\langle 0\left|T\left{\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right}\right| 0\right\rangle=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 i v} e^{-i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)}\left[e^{i \omega_k \tau} \theta(-\tau)+e^{-i \omega_k \tau} \theta(\tau)\right]
$$
物理代考|量子场论代考Quantum field theory代考|Lagrangian derivation
In Section 2.3 we showed that free quantum fields satisfy
$$
\begin{aligned}
{\left[\phi(\vec{x}, t), \phi\left(\vec{x}^{\prime}, t\right)\right] } & =0, \
{\left[\phi(\vec{x}, t), \partial_t \phi\left(\vec{x}^{\prime}, t\right)\right] } & =i \hbar \delta^3\left(\vec{x}-\vec{x}^{\prime}\right)
\end{aligned}
$$
(we have temporarily reinstated $\hbar$ to clarify the classical limit). We also showed that free quantum fields satisfy the free scalar field Euler-Lagrange equation $\left(\square+m^2\right) \phi=0$. In an arbitrary interacting theory, we must generalize these equations to specify how the dynamics is determined. In quantum mechanics, this is done with the Hamiltonian. So, one natural approach is to assume that $i \partial_t \phi(x)=[\phi, H]$ for an interacting quantum field theory, which leads to the Hamiltonian derivation of the Feynman rules in Section 7.2. In this section we discuss the simpler Lagrangian approach based on the Schwinger-Dyson equations, which has the advantage of being manifestly Lorentz invariant from start to finish.
In the Lagrangian approach, Hamilton’s equations are replaced by the Euler-Lagrange equations. We therefore assume that our interacting fields satisfy the Euler-Lagrange equations derived from a Lagrangian $\mathcal{L}$ (the generalization of $\left(\square+m^2\right) \phi=0$ ), just like classical fields. We will also assume Eqs. (7.3) and (7.4) are still satisfied. This is a natural assumption, since at any given time the Hilbert space for the interacting theory is the same as that of a free theory. Equation (7.3) is a necessary condition for causality: at the same time but at different points in space, all operators, in particular fields, should be simultaneously observable and commute (otherwise there could be faster-than-light communication). This causality requirement will be discussed more in the context of the spin-statistics theorem in Section 12.6. Equation (7.4) is the equivalent of the canonical commutation relation from quantum mechanics: $[\hat{x}, \hat{p}]=i \hbar$. It indicates that a quantity and its time derivative are not simultaneously observable – the hallmark of the uncertainty principle.
At this point we only know how to calculate $\left\langle 0\left|T\left{\phi(x) \phi\left(x^{\prime}\right)\right}\right| 0\right\rangle$ in the free theory. To calculate this commutator in an interacting theory, it is helpful to have the intermediate result
$$
\left(\square+m^2\right)\left\langle\Omega\left|T\left{\phi(x) \phi\left(x^{\prime}\right)\right}\right| \Omega\right\rangle=\left\langle\Omega\left|T\left{\left(\square+m^2\right) \phi(x) \phi\left(x^{\prime}\right)\right}\right| \Omega\right\rangle-i \hbar \delta^4\left(x-x^{\prime}\right),
$$
where $|\Omega\rangle$ is the vacuum in the interacting theory. The $\delta^4\left(x-x^{\prime}\right)$ on the right side of this equation is critically important. It signifies the difference between the classical and quantum theories in a way that will be clear shortly.
量子场论代考
物理代考|量子场论代考Quantum field theory代考|The Feynman propagator
回顾一下,我们的直接目标,正如第5章所述,是计算截面,这是由$S$ -矩阵元素决定的。我们现在有了一个表达式,LSZ约简公式,对于$S$ -矩阵元素,用时间顺序的域积表示。接下来,我们需要弄清楚如何计算这些时间顺序的乘积。作为一个例子,我们现在将计算自由理论中的时间顺序乘积。在第七章中,我们将利用摄动理论推导出一种计算相互作用理论中时间顺序积的方法。
我们从自由场算子开始:
$$
\phi_0(x, t)=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{\sqrt{2 \omega_k}}\left(a_k e^{-i k x}+a_k^{\dagger} e^{i k x}\right),
$$
其中$k_0=\omega_k=\sqrt{m^2+\vec{k}^2}$、$a_k$和$a_k^{\dagger}$是时间无关的(所有时间相关的都在相位中)。然后,用$|0\rangle$代替$|\Omega\rangle$来表示自由理论中的真空,
$$
\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle=\int \frac{d^3 k_1}{(2 \pi)^3} \int \frac{d^3 k_2}{(2 \pi)^3} \frac{1}{\sqrt{2 \omega_{k_1}}} \frac{1}{\sqrt{2 \omega_{k_2}}}\left\langle 0\left|a_{k_1} a_{k_2}^{\dagger}\right| 0\right\rangle e^{i\left(k_2 x_2-k_1 x_1\right)} .
$$
$\left\langle 0\left|a_{k_1} a_{k_2}^{\dagger}\right| 0\right\rangle$给出$(2 \pi)^3 \delta^3\left(\vec{k}_1-\vec{k}_2\right)$,因此
$$
\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k} e^{i k\left(x_2-x_1\right)} .
$$
现在,我们对$\left\langle 0\left|T\left{\phi\left(x_1\right) \phi\left(x_2\right)\right}\right| 0\right\rangle$感兴趣。回想一下,时间排序将后面的字段放在左边,我们得到
$$
\begin{aligned}
\left\langle 0\left|T\left{\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right}\right| 0\right\rangle & =\left\langle 0\left|\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right| 0\right\rangle \theta\left(t_1-t_2\right)+\left\langle 0\left|\phi_0\left(x_2\right) \phi_0\left(x_1\right)\right| 0\right\rangle \theta\left(t_2-t_1\right) \
& =\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k}\left[e^{i k\left(x_2-x_1\right)} \theta\left(t_1-t_2\right)+e^{i k\left(x_1-x_2\right)} \theta\left(t_2-t_1\right)\right] \
& =\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 \omega_k}\left[e^{i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)} e^{-i \omega_k \tau} \theta(\tau)+e^{-i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)} e^{i \omega_k \tau} \theta(-\tau)\right],
\end{aligned}
$$
其中$\tau=t_1-t_2$。第一项取$k \rightarrow-k$使体积积分$\int d^3 k$不变,得到
$$
\left\langle 0\left|T\left{\phi_0\left(x_1\right) \phi_0\left(x_2\right)\right}\right| 0\right\rangle=\int \frac{d^3 k}{(2 \pi)^3} \frac{1}{2 i v} e^{-i \vec{k}\left(\vec{x}_1-\vec{x}_2\right)}\left[e^{i \omega_k \tau} \theta(-\tau)+e^{-i \omega_k \tau} \theta(\tau)\right]
$$
物理代考|量子场论代考Quantum field theory代考|Lagrangian derivation
在2.3节中,我们证明了自由量子场满足
$$
\begin{aligned}
{\left[\phi(\vec{x}, t), \phi\left(\vec{x}^{\prime}, t\right)\right] } & =0, \
{\left[\phi(\vec{x}, t), \partial_t \phi\left(\vec{x}^{\prime}, t\right)\right] } & =i \hbar \delta^3\left(\vec{x}-\vec{x}^{\prime}\right)
\end{aligned}
$$
(我们暂时恢复$\hbar$以澄清经典极限)。我们还证明了自由量子场满足自由标量场欧拉-拉格朗日方程$\left(\square+m^2\right) \phi=0$。在任意的相互作用理论中,我们必须推广这些方程来说明动力学是如何确定的。在量子力学中,这是用哈密顿量来完成的。因此,一种自然的方法是假设$i \partial_t \phi(x)=[\phi, H]$是一个相互作用的量子场论,这导致了第7.2节中费曼规则的哈密顿推导。在本节中,我们讨论基于Schwinger-Dyson方程的更简单的拉格朗日方法,它具有从头到尾明显的洛伦兹不变的优点。
在拉格朗日方法中,汉密尔顿方程被欧拉-拉格朗日方程所取代。因此,我们假设我们的相互作用场满足由拉格朗日方程$\mathcal{L}$ ($\left(\square+m^2\right) \phi=0$的推广)导出的欧拉-拉格朗日方程,就像经典场一样。我们也会假设等式。(7.3)和(7.4)仍然满意。这是一个自然的假设,因为在任何给定时间,相互作用理论的希尔伯特空间与自由理论的希尔伯特空间是相同的。式(7.3)是因果关系的必要条件:在同一时间,但在空间的不同点上,所有的算子,在特定的领域,应该同时被观察和交换(否则可能会有超光速通信)。这个因果关系要求将在第12.6节的自旋统计定理中进行更多的讨论。式(7.4)等价于量子力学中的正则换易关系:$[\hat{x}, \hat{p}]=i \hbar$。它表明一个量和它的时间导数不是同时可观测的——这是测不准原理的标志。
在这一点上,我们只知道如何计算$\left\langle 0\left|T\left{\phi(x) \phi\left(x^{\prime}\right)\right}\right| 0\right\rangle$在自由理论。为了在相互作用理论中计算换向子,有中间结果是有帮助的
$$
\left(\square+m^2\right)\left\langle\Omega\left|T\left{\phi(x) \phi\left(x^{\prime}\right)\right}\right| \Omega\right\rangle=\left\langle\Omega\left|T\left{\left(\square+m^2\right) \phi(x) \phi\left(x^{\prime}\right)\right}\right| \Omega\right\rangle-i \hbar \delta^4\left(x-x^{\prime}\right),
$$
$|\Omega\rangle$是相互作用理论中的真空。等式右边的$\delta^4\left(x-x^{\prime}\right)$是至关重要的。它标志着经典理论和量子理论之间的区别,我们很快就会明白。

物理代考|量子场论代考Quantum field theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。