MY-ASSIGNMENTEXPERT™可以为您提供math Math46400 Number theory 数论的代写代考和辅导服务!
这是纽约市立学院数论课程的代写成功案例。
Math46400简介
A first course in algebraic number theory which assumes some abstract algebra. Topics include: unique factorization in the integers and Euclidean domains, structure of the groups Z/mZ and their multiplicative units, quadratic residues and quadratic reciprocity, algebraic number fields, finite fields.
Prerequisites: Grade of C or better in MATH 34700 or departmental permission.
Contact Hours: 4 hr./wk.
Credits: 4
This is an undergraduate version of Math A6400. You must take the graduate version if you want graduate credit.
Prerequisites
Number theory or arithmetic or higher arithmetic in older usage is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, “Mathematics is the queen of the sciences—and number theory is the queen of mathematics.”
Math46400 Number theory HELP(EXAM HELP, ONLINE TUTOR)
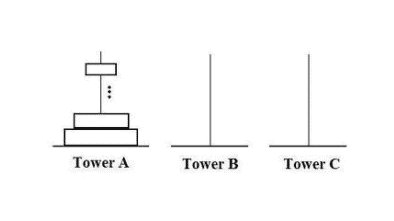
Prove a formula for the least number of moves required to move a Tower of Hanoi with $n$ disks to another pole.
Solution:
We shall prove using induction that the least number of moves is $2^n-1$, for all $n \geq 1$. The base case is trivial: if you only have one disk, then it only takes one move to take one disk to another pole.
Now, suppose that the least number of moves to take a tower of $n$ disks to another pole is exactly $2^n-1$. Let us suppose that we have a tower of $n+1$ disks. In order to move the tower, we will eventually have to move the last disk at the bottom of the pile. In order to access the last disk, we first need to move the $n$ disks on top to another pole. Notice that we need them all in one single pole to allow space to move the largest disk to another pole. This will take at least $2^n-1$ moves, by the induction hypothesis. Then we can move the $(n+1)$ th disk to another pole (at least 1 extra move) and, last, we need to move the other $n$ disks back on top of the largest disk. This last procedure is identical
(a) Show that $n ! \leq n^n$ for all $n>0$.
(b) $(n+1)^{(n-1)} \leq n^n$ for all $n>0$.
Solution:
(a). For $n=1$ we have $1 !=1 \leq 1^1=1$. Now suppose that $n ! \leq n^n$. Then:
$$
(n+1) !=(n+1) \cdot n ! \leq(n+1) n^n \leq(n+1)(n+1)^n \leq(n+1)^{(n+1)},
$$
since $n<(n+1)$. Therefore, by the principle of mathematical induction, the result is true for all $n \geq 1$.
(b). Let us start with the base case $n=1: 1=2^0 \leq 1^1=1$. Now, let us assume that $(n+1)^{(n-1)} \leq n^n$ for some $n \geq 1$. Equivalently, we may assume that:
$$
\left(\frac{n+1}{n}\right)^n \leq n+1 \text {. }
$$
We shall prove that:
$$
\left(\frac{n+2}{n+1}\right)^{n+1} \leq^? n+2 .
$$
Indeed, notice that $\frac{n+2}{n+1} \leq \frac{n+1}{n}$, for all $n \geq 1$ and therefore:
$$
\begin{aligned}
\left(\frac{n+2}{n+1}\right)^{n+1} & =\left(\frac{n+2}{n+1}\right)^n \cdot\left(\frac{n+2}{n+1}\right) \leq\left(\frac{n+1}{n}\right)^n \cdot\left(\frac{n+2}{n+1}\right) \
& \leq(n+1) \cdot \frac{(n+2)}{(n+1)} \leq n+2 .
\end{aligned}
$$
Therefore, by the principle of mathematical induction, the result is true for all $n \geq 1$.
Note: Have you noticed how HARD it is to prove, using Calculus, that the function $F(x)=(x+1)^{(x-1)}$ is less than $G(x)=x^x$ ? However, induction makes it easy!
What is wrong with the following proof? Theorem. All babies have the same color eyes. “Proof”. The base case is clear: one baby has the same color eyes as helself or himself. Now suppose we have $n+1$ babies, and name them $\left{B_1, \ldots, B_n, B_{n+1}\right}$. By the induction hypothesis, the babies in sets $\left{B_1, \ldots, B_n\right}$ and those in $\left{B_2, \ldots, B_{n+1}\right}$ have the same color eyes, and hence all of the babies $B_1, \ldots, B_{n+1}$ have the same color eyes.
Solution:
The problem is at the base case. The theorem can be restated as “Any subset of $n$ babies have the same color eyes”. Since the statement is a comparison among babies, the base case should be the case $n=2$, and not the case $n=1$. In other words, to use the induction step mentioned in the “proof”, one would have to first prove the case $n=2$ : any two babies have the same color eyes. But, of course, this is already false.
Prove that any natural number $n \geq 2$ either is a prime or factors into a product of primes.
Solution:
We shall prove this using complete induction. The base case $n=2$ is clear, since 2 is prime. Now suppose that all integers $2 \leq k<n$ are either a prime or factor into a product of primes. If $n$ is prime, then we are done. Otherwise, if $n$ is not prime, then it is composite. Thus there exist positive integers $a, b$ with $1<a, b<n$ and $n=a \cdot b$. By the induction hypothesis, both $a$ and $b$ are either primes or a product of primes, and hence $n=a b$ is a product of primes. Hence, the induction step is proven, and by the Principle of Mathematical Induction, the property is true for all $n \geq 2$.

MY-ASSIGNMENTEXPERT™可以为您提供MATH MATH46400 NUMBER THEORY 数论的代写代考和辅导服务!