MY-ASSIGNMENTEXPERT™可以为您提供online STAT501 Linear RegressioN线性回归的代写代考和辅导服务!
这是宾夕法尼亚州立大学线性回归课程的代写成功案例。
STAT501 课程简介
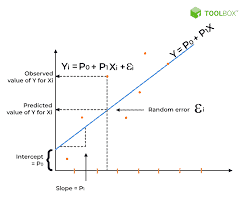
This graduate level course offers an introduction into regression analysis. A researcher is often interested in using sample data to investigate relationships, with an ultimate goal of creating a model to predict a future value for some dependent variable. The process of finding this mathematical model that best fits the data involves regression analysis.
STAT 501 is an applied linear regression course that emphasizes data analysis and interpretation. Generally, statistical regression is collection of methods for determining and using models that explain how a response variable (dependent variable) relates to one or more explanatory variables (predictor variables).
Prerequisites
This graduate level course covers the following topics:
- Understanding the context for simple linear regression.
- How to evaluate simple linear regression models
- How a simple linear regression model is used to estimate and predict likely values
- Understanding the assumptions that need to be met for a simple linear regression model to be valid
- How multiple predictors can be included into a regression model
- Understanding the assumptions that need to be met when multiple predictors are included in the regression model for the model to be valid
- How a multiple linear regression model is used to estimate and predict likely values
- Understanding how categorical predictors can be included into a regression model
- How to transform data in order to deal with problems identified in the regression model
- Strategies for building regression models
- Distinguishing between outliers and influential data points and how to deal with these
- Handling problems typically encountered in regression contexts
- Alternative methods for estimating a regression line besides using ordinary least squares
- Understanding regression models in time dependent contexts
- Understanding regression models in non-linear contexts
STAT501 Linear Regression HELP(EXAM HELP, ONLINE TUTOR)
Let $X$ be a random variable that you know is in the range $[-1,2]$ and you know has expected value of $\mathbf{E}[X]=0$. Use the Markov Inequality to upper bound $\operatorname{Pr}[X>1.5]$ ?
(Hint: you will need to use a change of variables.)
Consider a matrix
$$
A=\left[\begin{array}{ccc}
2 & 2 & 3 \
-2 & 7 & 4 \
-3 & -3 & -6 \
-8 & 2 & 3
\end{array}\right]
$$
(a) Add a column to $A$ so that it is invertable.
(b) Remove a row from $A$ so that it is invertable.
(c) Is $A A^T$ invertable?
(d) Is $A^T A$ invertable?
[50 points] Let the first column of the data set be the explanatory variable $\mathrm{x}$, and let the fourth column be the dependent variable $\mathrm{y}$.
(a) [10 points] Run simple linear regression to predict y from x. Report the linear model you found. Predict the value of $\mathrm{y}$ for new $\mathrm{x}$ values 1 , for 2 , and for 3 .
(b) [10 points] Use cross-validation to predict generalization error, with error of a single data point $(\mathrm{x}, \mathrm{y})$ from a model $M$ as $(M(\mathrm{x})-\mathrm{y})^2$. Describe how you did this, and which data was used for what.
(c) [20 points] On the same data, run polynomial regression for $p=2,3,4,5$. Report polynomial models for each. With each of these models, predict the value of $\mathrm{y}$ for a new $\mathrm{x}$ values of 1 , for 2 , and for 3 .
(d) [10 points] Cross-validate to choose the best model. Describe how you did this, and which data was used for what.
[25 points] Now let the first three columns of the data set be separate explanatory variables $\mathrm{x} 1, \mathrm{x} 2, \mathrm{x} 3$. Again let the fourth column be the dependent variable $\mathrm{y}$.
- Run linear regression simultaneously using all three explanatory variables. Report the linear model you found. Predict the value of $y$ for new $(\mathrm{x} 1, \mathrm{x} 2, \mathrm{x} 3)$ values $(1,1,1)$, for $(2,0,4)$, and for $(3,2,1)$.
- Use cross-validation to predict generalization error, with error of a single data point ( $\mathrm{x} 1$, $\mathrm{x} 2, \mathrm{x} 3, \mathrm{y})$ from a model $M$ as $(M(\mathrm{x} 1, \mathrm{x} 2, \mathrm{x} 3)-\mathrm{y})^2$. Describe how you did this, and which data was used for what.
[25 points] Consider two functions
$$
f_1(x, y)=(x-2)^2+(y-3)^2 \quad f_2(x, y)=(1-(y-3))^2+20\left((x+3)-(y-3)^2\right)^2
$$
Starting with $(x, y)=(0,0)$ run the gradient descent algorithm for each function. Run for $T$ iterations, and report the function value at the end of each step.
(a) First, run with a fixed learning rate of $\gamma=0.5$.
(b) Second, run with any variant of gradient descent you want. Try to get the smallest function value after $T$ steps.
For $f_1$ you are allowed only $T=10$ steps. For $f_2$ you are allowed $T=100$ steps.
[ +5 points] If any students do significantly better than the rest of the class on $f_2$ in part (b), we will award up to 5 extra credit points.

MY-ASSIGNMENTEXPERT™可以为您提供ONLINE STAT501 LINEAR REGRESSION线性回归的代写代考和辅导服务!