如果你也在 怎样代写随机过程Stochastic Process这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。随机过程Stochastic Process是描述随机现象在时间上的演变的任何过程。从数学的角度来看,随机过程的理论在1950年左右得到解决。从那时起,随机过程已经成为数学家、物理学家、工程师和其他研究人员的一个常用工具。
数学家、物理学家和工程师的常用工具,该理论的应用领域包括股票定价建模、合理期权定价理论和微分几何。
一个随机过程,也被称为随机过程,是一个由一些数学集合索引的随机变量的集合。每个概率和随机过程都与该集合中的一个元素唯一相关。索引集是用于索引随机变量的集合。索引集传统上是实线的一个子集,如自然数,这为索引集提供了时间解释。
随机过程的含义是指有一个系统,在一定时间内有观察结果,而结果,也就是每个时间的观察值是一个随机变量。
数值集合中的每个随机变量都取自同一个数学空间,称为状态空间。例如,这个状态空间可以是整数、实线或$eta$-dimensional Euclidean空间。一个随机过程的增量是一个随机过程在两个索引值之间的变化量,这两个索引值经常被解释为两个时间点。由于其随机性,一个随机过程可以有许多结果,而一个随机过程的单一结果被称为,除其他外,一个样本函数或实现。
A population starts with one individual at time $n=0: Z_{0}=1$.
After one unit of time (at time $n=1$ ) the sole individual produces $Z_{1}$ identical clones of itself and dies. $Z_{1}$ is an $\mathbb{N}_{0}$-valued random variable.
(a) If $Z_{1}$ happens to be equal to 0 the population is dead and nothing happens at any future time $n \geq 2$.
(b) If $Z_{1}>0$, a unit of time later, each of $Z_{1}$ individuals gives birth to a random number of children and dies. The first one has $Z_{1,1}$ children, the second one $Z_{1,2}$ children, etc. The last, $Z_{1}^{\text {th }}$ one, gives birth to $Z_{1, Z_{1}}$ children. We assume that the distribution of the number of children is the same for each individual in every generation and independent of either the number of individuals in the generation and of the number of children the others have. This distribution, shared by all $Z_{n, i}$ and $Z_{1}$, is called the offspring distribution. The total number of individuals in the second generation is now
$$
Z_{2}=\sum_{k=1}^{Z_{1}} Z_{1, k}
$$
(c) The third, fourth, etc. generations are produced in the same way. If it ever happens that $Z_{n}=0$, for some $n$, then $Z_{m}=0$ for all $m \geq n$ – the population is extinct. Otherwise,
$$
Z_{n+1}=\sum_{k=1}^{Z_{n}} Z_{n, k}
$$
my-assignmentexpert™ 随机过程Stochastic Process作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的随机过程Stochastic Process作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此随机过程Stochastic Process作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计Statistics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在随机过程Stochastic Process代写方面经验极为丰富,各种随机过程Stochastic Process相关的作业也就用不着 说。
我们提供的随机过程Stochastic Process及其相关学科的代写,服务范围广, 其中包括但不限于:
- 时间序列分析Time-Series Analysis
- 马尔科夫过程 Markov process
- 随机最优控制stochastic optimal control
- 粒子滤波 Particle Filter
- 采样理论 sampling theory
数学代写| 随机过程作业代写Stochastic Process代考|Law of Large Numbers
Let $X_{1}, X_{2}, \ldots$ be a sequence of identically distributed random variables, and let $g: \mathbb{R} \rightarrow \mathbb{R}$ be function such that $\mu=\mathbb{E}\left[g\left(X_{1}\right)\right]\left(=\mathbb{E}\left[g\left(X_{2}\right)\right]=\ldots\right)$ exists. Then
$$
\frac{g\left(X_{1}\right)+g\left(X_{2}\right)+\cdots+g\left(X_{n}\right)}{n} \rightarrow \mu=\int_{-\infty}^{\infty} g(x) f_{X_{1}}(x) d x, \text { as } n \rightarrow \infty
$$
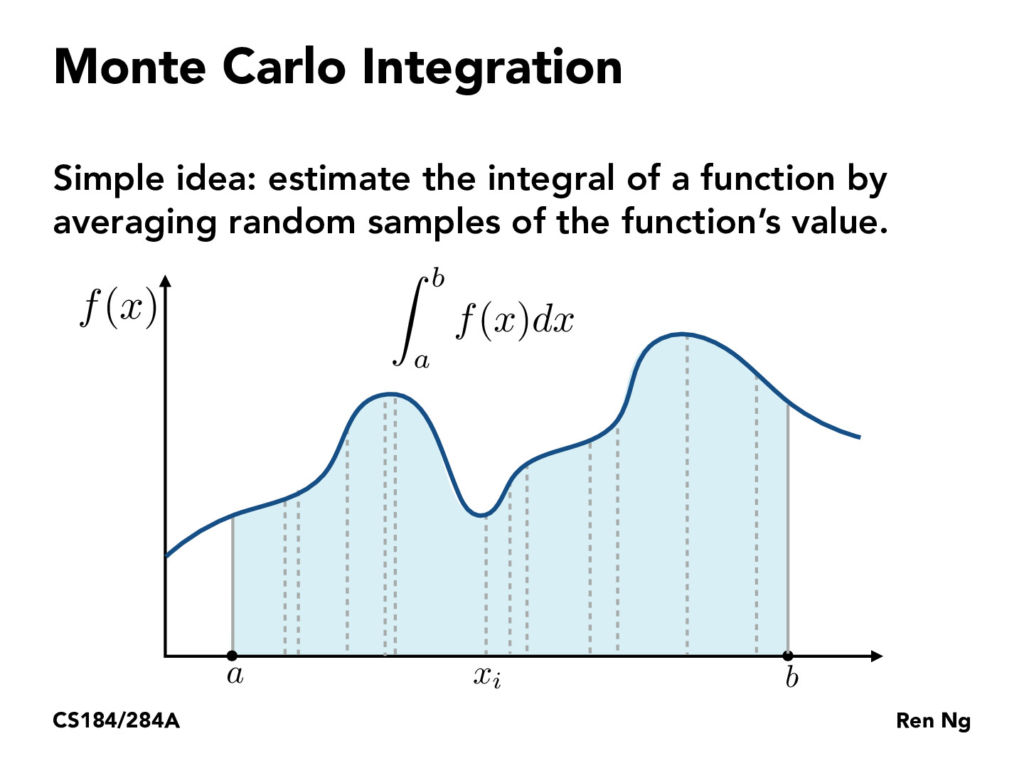
The key idea of Monte Carlo integration is the following
Suppose that the quantity $y$ we are interested in can be written as $y=\int_{-\infty}^{\infty} g(x) f_{X}(x) d x$ for some random variable $X$ with density $f_{X}$ and come function $g$, and that $x_{1}, x_{2}, \ldots$ are random numbers distributed according to the distribution with density $f_{X}$. Then the average
$$
\frac{1}{n}\left(g\left(x_{1}\right)+g\left(x_{2}\right)+\cdots+g\left(x_{n}\right)\right),
$$
will approximate $y$.
It can be shown that the accuracy of the approximation behaves like $1 / \sqrt{n}$, so that you have to quadruple the number of simulations if you want to double the precision of you approximation.
数学代写| 随机过程作业代写STOCHASTIC PROCESS代考|numerical integration
- (numerical integration) Let $g$ be a function on $[0,1]$. To approximate the integral $\int_{0}^{1} g(x) d x$ we can take a sequence of $n(\mathrm{U}[0,1])$ random numbers $x_{1}, x_{2}, \ldots$,
$$
\int_{0}^{1} g(x) d x \approx \frac{g\left(x_{1}\right)+g\left(x_{2}\right)+\cdots+g\left(x_{n}\right)}{n}
$$
because the density of $X \sim U[0,1]$ is given by
$$
f_{X}(x)= \begin{cases}1, & 0 \leq x \leq 1 \ 0, & \text { otherwise }\end{cases}
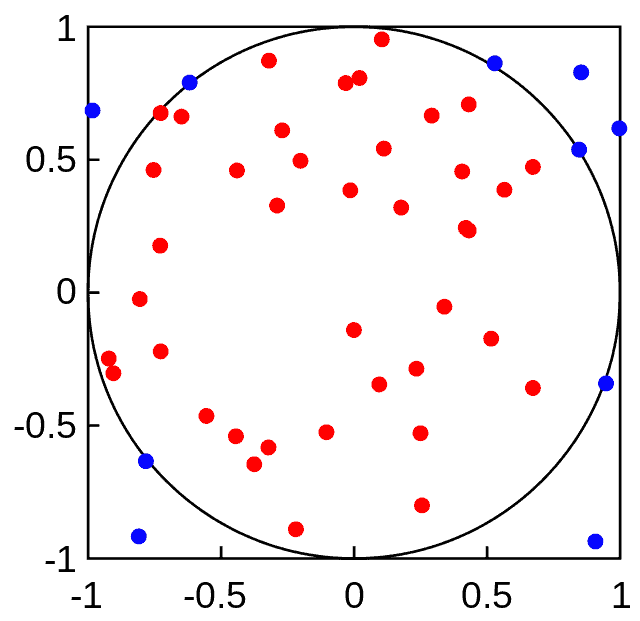
$$ - (estimating probabilities) Let $Y$ be a random variable with the density function $f_{Y}$. If we are interested in the probability $\mathbb{P}[Y \in[a, b]]$ for some $a<b$, we simulate $n$ draws $y_{1}, y_{2}, \ldots, y_{n}$ from the distribution $F_{Y}$ and the required approximation is
$$
\mathbb{P}[Y \in[a, b]] \approx \frac{\text { number of } y_{n} \text { ‘s falling in the interval }[a, b]}{n} .
$$
One of the nicest things about the Monte-Carlo method is that even if the density of the random variable is not available, but you can simulate draws from it, you can still preform the calculation above and get the desired approximation. Of course, everything works in the same way for probabilities involving random vectors in any number of dimensions.
随机过程代考
数学代写| 随机过程作业代写STOCHASTIC PROCESS代考|LAW OF LARGE NUMBERS
设是一串相同分布的随机变量,设是函数,以便存在。那么$g: \mathbb{R} \rightarrow \mathbb{R}$ be function such that $\mu=\mathbb{E}\left[g\left(X_{1}\right)\right]\left(=\mathbb{E}\left[g\left(X_{2}\right)\right]=\ldots\right)$ exists. Then
$$
\frac{g\left(X_{1}\right)+g\left(X_{2}\right)+\cdots+g\left(X_{n}\right)}{n} \rightarrow \mu=\int_{-\infty}^{\infty} g(x) f_{X_{1}}(x) d x, \text { as } n \rightarrow \infty
$$
蒙特卡洛积分的关键思想如下
假设我们感兴趣的数量可以写成:$y=\int_{-\infty}^{\infty} g(x) f_{X}(x) d x$对于一些具有密度和来函数的随机变量,并且是按照密度分布的随机数。那么平均数
$$
\mathbb{P}[Y \in[a, b]] \approx \frac{\text { number of } y_{n} \text { ‘s falling in the interval }[a, b]}{n} .
$$
将近似于 .
可以证明,近似的精度表现为 ,因此,如果你想把近似的精度提高一倍,你就必须把模拟的次数增加四倍。
数学代写| 随机过程作业代写STOCHASTIC PROCESS代考|NUMERICAL INTEGRATION
设是一个在…上的函数。为了近似该积分,我们可以取一串随机数,
因为的密度是由
设是一个随机变量,其密度函数为 . 如果我们对某一概率感兴趣,我们从分布中模拟抽取,所需的近似值是
蒙特卡洛方法最棒的一点是,即使随机变量的密度不可用,但你可以模拟它的抽样,你仍然可以预先进行上述计算并得到所需的近似值。当然,对于涉及任何数量维度的随机向量的概率,一切都以同样的方式进行。

数学代写| 随机过程作业代写Stochastic Process代考|Random variables 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
统计代考
统计是汉语中的“统计”原有合计或汇总计算的意思。 英语中的“统计”(Statistics)一词来源于拉丁语status,是指各种现象的状态或状况。
数论代考
数论(number theory ),是纯粹数学的分支之一,主要研究整数的性质。 整数可以是方程式的解(丢番图方程)。 有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。 透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)
数值分析代考
数值分析(Numerical Analysis),又名“计算方法”,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。 它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。