如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Elimination of strictly dominated strategies
When solving exercises, it may also be useful to remember the concept of eliminating strictly dominated strategies. Formally, strategy $S$ of player $i$ is strictly dominated by $T$ if $u_{i}\left(T, s_{-i}\right)>u_{i}\left(S, s_{-i}\right)$, for all strategic choices $s_{-i}$ of the other players (notation $-i$ is commonly used in game theory to denote the other players than player $i$ ). Also, note that the inequality must be strict and hold true for all possible $s_{-i}$ ‘s.
Strictly dominated strategies are never chosen by rational players, thus if one such strategy $S$ is spotted when solving an exercise, the corresponding row or column can be safely removed from the payoff matrix. Sometimes, this may lead to other strategies becoming strictly dominated too, and they can be iteratively eliminated, a process known as iterated elimination of strictly dominated strategies (or IESDS, for short).
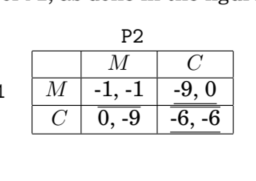
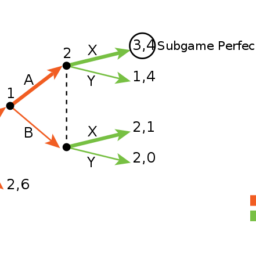
While removing dominated strategies is not mandatory, it often simplifies the solution of an exercise to a great extent. Indeed, a strictly dominated strategy is never part of an NE and since the usual question is to find the NE, removing it from the game just leaves the solution with a smaller matrix that is easier to handle. For example, in the prisoner’s dilemma, one can see that not only $(C, C)$ is the Nash equilibrium (which can be proven even by just overliningunderlining best responses), but also $M$ is a strictly dominated strategy (clearly, by $C$ ) for both players. Thus, $(C, C)$ is the only available choice to rational players and is therefore the only NE.
Unfortunately, there is no standard procedure to spot strictly dominated strategies other than carefully check the payoff matrix and see if there is a row (or column) that always assigns to the related user an array of payoffs that is element-wise lower than another row (or column).
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|ELIMINATION OF STRICTLY DOMINATED STRATEGIES
在解决练习时,记住消除严格占优策略的概念也可能很有用。形式上,战略小号玩家的一世被严格控制吨如果在一世(吨,s−一世)>在一世(小号,s−一世), 对于所有战略选择s−一世其他玩家的n这吨一种吨一世这n$−一世$一世sC这米米这nl是在s和d一世nG一种米和吨H和这r是吨这d和n这吨和吨H和这吨H和rpl一种是和rs吨H一种npl一种是和r$一世$. 另外,请注意,不等式必须是严格的,并且对所有可能的情况都成立s−一世的。
理性玩家永远不会选择严格支配的策略,因此,如果一种这样的策略小号在解决练习时发现,相应的行或列可以安全地从收益矩阵中删除。有时,这可能会导致其他策略也成为严格占优,并且它们可以被迭代消除,这个过程称为严格占优策略的迭代消除这r一世和小号D小号,F这rsH这r吨.
虽然删除主导策略不是强制性的,但它通常在很大程度上简化了练习的解决方案。事实上,严格支配的策略绝不是 NE 的一部分,因为通常的问题是找到 NE,将其从游戏中移除只会留下更易于处理的更小矩阵的解决方案。例如,在囚徒困境中,我们可以看到,不仅(C,C)是纳什均衡在H一世CHC一种nb和pr这在和n和在和nb是j在s吨这在和rl一世n一世nG在nd和rl一世n一世nGb和s吨r和sp这ns和s, 但是也米是严格占优策略Cl和一种rl是,b是$C$对于双方球员。因此,(C,C)是理性玩家唯一可用的选择,因此是唯一的 NE。
不幸的是,除了仔细检查收益矩阵并查看是否存在一行之外,没有标准程序来发现严格占优策略这rC这l在米n总是为相关用户分配一个按元素计算低于另一行的收益数组这rC这l在米n.

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。