如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Lotteries
Stage games are often chosen as simple 2-person static games of complete information. They can be a modified version of well known games such as the prisoner’s dilemma, the coordination game, or the discoordination game. Multistage games are meant to capture the strategic impact of current actions of some players to the future actions of other players.
This is done by combining individual smaller games, assuming that they are always played by the same agents, and that the payoffs of the stage games are aggregated in some way. The most common approach is to consider that discounted versions of the local payoffs are cumulated to get the total payoff in the grand game. The discount factor $\delta$ is a value between 0 and 1 that reflects how much players care about the future. In economics, this is usually connected to resource decay or inflation of prices. But another appealing interpretation assumes that players can also abandon the game earlier than the envisioned time horizon and connects $\delta$ with the expected time spent in the system (the lower $\delta$, the earlier the player leaves the game).
Some problems consider a multistage version made of different games combined together. For the sake of simplicity, these cases are usually limited to the aggregate of two different stage games. However, it is also very common to consider repeated games, in which the same stage game is played multiple times, and in this case it is common to see the game repeated for more than 2 times. Actually, a very interesting case is that of the game being repeated with an infinite horizon. While this is impractical to consider for the aggregate of different games, it is definitely the most common case for repeated game scenarios, especially if the underlying model is not that the players are actually doomed to play a game for all eternity, but actually they do not know the last stage of their interaction (see again the connection between $\delta$ and their probability of hanging out in the system for the next round).
经济代写|博弈论作业代写GAME THEORY代考|Finite horizon
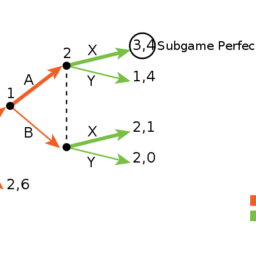
The solution approach for finite horizon is analogous to backward induction. One must consider the last stage, since in that case there is no impact on future decisions, which are non-existent, and therefore the players simply choose an NE (i.e., they very selfishly act like “there is no tomorrow”). Then, this conclusion is propagated back to the penultimate stage and so on.
This leads to different conclusions depending on the numbers of NEs in the stage games. If the last stage game has a single $\mathrm{NE}$, then the rational players are fully aware of that and they all know that this will be what they are going to play in the end. Thus, the last stage can be safely removed from the analysis by “merging” it with the upper layers and the game just become shorter.
In the particular case that all stage games have a single NE, as is the case for a repeated version of a static game with a single NE, the conclusion is immediate, but not very interesting. The only rational outcome is that this single NE is played at every stage, and there is no strategic extension in the unfolding over time, beyond what already given by a one-shot game. Notably, the repetition of the NE at every stage will also lead to an SPE, since an NE is played in every subgame. But just keep in mind that an SPE will require some more details to be specified, such as what happens off the equilibrium path – this is immediate to determine, since what happens is that the only NE of the stage game is played there too, it is just that it is easy to forget to mention it.
If there are multiple NEs available instead, some strategic variants become available, and this implies that some non-NE outcomes of the stage game can be played. Naturally, this cannot happen for the last stage, which is bound to be played as an NE, but the choice among multiple NEs in the last stage may even create some “carrot and stick” options where players create a collaborative outcome in the earlier rounds. This happens by defining one good NE of the last round as the ultimate reward (carrot) and a bad NE of the last round as a punishment (stick) and anticipating that cooperation in the earlier stages will be rewarded, while defection will be punished.
For this approach to work, some conditions are required. First, the difference between reward and punishment must be high enough. And at the same time, the discount factor, if present, ought to be high enough to make the punishment credible. This is particularly evident if $\delta$ is low since the players will care little about the future; in particular, if the interpretation of a low $\delta$ is that they are likely to exit the system, they will consider this as their last stage, so there is no way to convince them to play something else than an NE.
Overall, the conditions for this approach to work are once again connected with the concept of credible threats. Since there is actually no communication and the interaction of punishment and/or reward only happens in the players’ heads, they can anticipate that a possible behavior is to get punished if they do not cooperate, but if this threat is non credible, they will dismiss it, so the dynamic outcome will not result in an SPE. Thus, the request to find an SPE in such cases translates into looking on whether these conditions support such a reward/punishment approach, which usually translates into a requirement on $\delta$ that must be above a certain value. Keep in mind that the standard case of playing an NE multiple times in every evolution of the game is also always present as an SPE.
经济代写|博弈论作业代写GAME THEORY代考|Infinitely repeated games
For the case of games that are repeated infinitely many times, the conclusion is even more interesting. Instead of requiring a credible reward and punishment approach made of two or more NEs with an explicit difference between each other, it can be created out of thin air by the so called “grim trigger” strategy. This is true even for repeated games with a single NE, and indeed it is often studied in application to the prisoner’s dilemma. Whatever the underlying stage game, it is usually assumed that the players have a cooperating and a defecting option, which in the case of the prisoner’s dilemma are to collaborate with police or stay silent, respectively. Only, cooperation is not an NE of the stage game, while mutual defection is.
In an iterated game that repeats such a stage game infinitely many times, it is found that playing the NE forever is of course a possible SPE. But also cooperation played forever can be established as an alternative SPE, or better, as its equilibrium path. To prove this, one cannot resort to an approach akin to backward induction, since there is actually no last stage to start from. The idea is that the players start with an initial cooperation and they “agree” (once again, this agreement is just in their head since they do not actually communicate) that deviating players will be punished for the rest of the game, which is forever. This is formally defined as a “grim trigger” strategy, which is to play cooperation as long as all previous stage results describe mutual cooperation, and to defect otherwise. It is called like that because once the trigger is pulled, there is no way back.
This strategy ought to establish cooperation being played forever as the equilibrium path. Yet, it does not fully prevent a player from deviating since selfish players are naturally tempted to adopt a myopic deviation, i.e., to play a deviation in the stage game. Such a deviation must exist and is actually the reason why the cooperating option is not a local Nash equilibrium in the first place. However, if this player also believes that the other player is adopting the grim trigger strategy, then the player anticipates that the myopic deviation will be advantageous for the current stage but will also lead to reduced payoffs in the future. Thus, the grim trigger is effective as long as the utility of cooperating forever is higher than taking a selfish deviation now and facing an eternal punishment in the future.
Notably, this depends as before on the difference between reward and punishment and also the value of the discount factor. If $\delta$ is low, even the threat of an eternal punishment may seem not credible – which may also well apply to ethical conclusions under a religious assumption. From a more mundane perspective of a game theoretic exercise, this means that very often the request
boils down to computing the minimum $\delta$ that establishes cooperation, which implies that the discount factor must fall into an interval like $\left(\delta_{\min }, 1\right)$ to have cooperation.
Beyond the standard case of the simple choice between cooperation and defection, more complex cases can be created whenever there are worse punishments available than eternal defection. Indeed, eternal defection may seem already scary enough, but there may be something like an immediate punishment and also eternal defection. This leads to an even lower required $\delta$ to establish cooperation. To better understand why, consider the following example that once again digresses into ethics. A social cooperation rule is generally established by threatening punishment. The more immediate, or the stronger, the punishment, the better the cooperation. If you want a society to behave well, for example, not cause global warming through environmental pollution, you can claim that this will lead to the disruption of the planet forever. Unfortunately, this eternal destruction of the planet does not seem very menacing for boomers whose life expectancy is low, and therefore they do not care much if they are going to leave a polluted Earth to their grandchildren. So, establishing an extra punishment in addition to that, like sending them to jail or causing them to pay a lot of money may be more effective.
The reasonings above can actually be extended also in the direction of not only obtaining just cooperation but a more involuted outcome thanks to Friedman’s theorem. Simply put, the theorem states that a scenario where players interact for infinitely many rounds can be driven to any linear combination of strategies that satisfies a certain condition if the discount factor is high enough. The condition is naturally that the resulting payoffs of all players must be better in a Pareto sense (i.e., element-wise) than the payoffs at the NE of the stage game. Clearly, it is impossible to convince a player to stick to a strategy that awards an eternally worse payoff than the one at the NE: at this point, the player would deviate and play the NE forever. However, any linear combination of moves (even over subsequent multiple rounds) that leads to an expected payoff higher than the NE for all players is sustainable as long as $\delta$ is high enough. The theorem essentially generalizes the reasoning of the grim trigger mentioned above to the case where the objective is not to play the basic cooperation, but possibly a mixed strategy and/or different strategies over multiple rounds.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|LOTTERIES
舞台游戏通常被选为简单的 2 人完全信息静态游戏。它们可以是众所周知的游戏的修改版本,例如囚徒困境、协调游戏或不协调游戏。多阶段游戏旨在捕捉某些玩家当前行为对其他玩家未来行为的战略影响。
这是通过组合单个较小的游戏来完成的,假设它们总是由相同的代理人玩,并且阶段游戏的收益以某种方式聚合。最常见的方法是考虑累积局部收益的折扣版本以获得大游戏中的总收益。折扣系数d是一个介于 0 和 1 之间的值,反映了玩家对未来的关心程度。在经济学中,这通常与资源衰退或价格上涨有关。但另一个吸引人的解释假设玩家也可以在预想的时间范围之前放弃游戏并连接d在系统中花费的预期时间吨H和l这在和r$d$,吨H和和一种rl一世和r吨H和pl一种是和rl和一种在和s吨H和G一种米和.
有些问题考虑了由不同游戏组合而成的多阶段版本。为简单起见,这些情况通常仅限于两个不同阶段游戏的聚合。然而,考虑重复游戏也很常见,其中同一阶段的游戏被玩了多次,在这种情况下,游戏重复超过 2 次是很常见的。实际上,一个非常有趣的例子是游戏以无限的视野重复。虽然这对于不同游戏的聚合考虑是不切实际的,但对于重复游戏场景来说,这绝对是最常见的情况,特别是如果底层模型不是玩家实际上注定要玩永恒的游戏,但实际上他们确实这样做了不知道他们互动的最后阶段s和和一种G一种一世n吨H和C这nn和C吨一世这nb和吨在和和n$d$一种nd吨H和一世rpr这b一种b一世l一世吨是这FH一种nG一世nG这在吨一世n吨H和s是s吨和米F这r吨H和n和X吨r这在nd.
经济代写|博弈论作业代写GAME THEORY代考|FINITE HORIZON
有限范围的求解方法类似于反向归纳。必须考虑最后一个阶段,因为在这种情况下,对未来的决策没有影响,这是不存在的,因此玩家只需选择一个 NE一世.和.,吨H和是在和r是s和lF一世sHl是一种C吨l一世ķ和“吨H和r和一世sn这吨这米这rr这在”. 然后,这个结论被传播回倒数第二阶段,依此类推。
这会根据阶段游戏中 NE 的数量得出不同的结论。如果最后阶段游戏有一个ñ和,那么理性的玩家都充分意识到了这一点,他们都知道这将是他们最终要玩的东西。因此,通过将最后阶段与上层“合并”,可以安全地从分析中移除最后阶段,游戏只会变得更短。
在所有阶段游戏都有一个 NE 的特殊情况下,就像重复版本的具有单个 NE 的静态游戏的情况一样,结论是立竿见影的,但不是很有趣。唯一合理的结果是,这个单一的 NE 在每个阶段都被播放,并且随着时间的推移展开,除了一次性游戏已经给出的策略扩展之外,没有战略延伸。值得注意的是,NE 在每个阶段的重复也会导致 SPE,因为在每个子游戏中都会播放 NE。但请记住,SPE 将需要指定更多细节,例如在平衡路径之外会发生什么——这是立即确定的,因为发生的情况是舞台游戏的唯一 NE 也在那里进行,它只是很容易忘记提及它。
如果有多个 NE 可用,则可以使用一些战略变体,这意味着可以玩一些非 NE 阶段游戏的结果。当然,这不可能发生在最后阶段,这必然是作为一个 NE 来玩的,但在最后阶段在多个 NE 之间进行选择甚至可能会产生一些“胡萝卜加大棒”的选择,让玩家在前几轮中创造出协作的结果. 这是通过将最后一轮的一个好的 NE 定义为最终奖励来实现的C一种rr这吨最后一轮的坏NE作为惩罚s吨一世Cķ并预计前期合作将得到奖励,而背叛将受到惩罚。
要使这种方法起作用,需要一些条件。首先,奖惩之间的差距必须足够高。同时,折扣系数(如果存在)应该足够高,以使惩罚可信。这尤其明显,如果d低,因为玩家很少关心未来;特别是,如果一个低的解释d是他们可能会退出系统,他们会认为这是他们的最后一个阶段,所以没有办法说服他们玩除了NE之外的其他东西。
总体而言,这种工作方法的条件再次与可信威胁的概念相关联。由于实际上没有交流,惩罚和/或奖励的相互作用只发生在玩家的头脑中,他们可以预期如果他们不合作,可能的行为是受到惩罚,但如果这种威胁是不可信的,他们会忽略它,因此动态结果不会导致 SPE。因此,在这种情况下寻找 SPE 的请求转化为查看这些条件是否支持这种奖励/惩罚方法,这通常转化为要求d必须高于某个值。请记住,在游戏的每次演变中多次使用 NE 的标准情况也始终以 SPE 的形式出现。
经济代写|博弈论作业代写GAME THEORY代考|INFINITELY REPEATED GAMES
对于无限重复游戏的情况,结论就更有趣了。它不需要由两个或多个彼此之间有明显差异的 NE 组成的可信奖励和惩罚方法,而是可以通过所谓的“冷酷触发”策略凭空创建。即使对于具有单个 NE 的重复博弈也是如此,并且确实经常研究它以应用于囚徒困境。无论底层的游戏是什么,通常都假设玩家有合作和背叛的选择,在囚徒困境的情况下,分别是与警察合作或保持沉默。只是,合作不是舞台游戏的NE,相互背叛才是。
在这样一个阶段性游戏无限次重复的迭代游戏中,发现永远玩NE当然是一种可能的SPE。但也可以将永久合作建立为替代 SPE,或者更好地作为其平衡路径。为了证明这一点,不能求助于类似于反向归纳的方法,因为实际上没有最后一个阶段可以开始。这个想法是玩家从最初的合作开始,他们“同意”这nC和一种G一种一世n,吨H一世s一种Gr和和米和n吨一世sj在s吨一世n吨H和一世rH和一种ds一世nC和吨H和是d这n这吨一种C吨在一种ll是C这米米在n一世C一种吨和偏离的玩家将在接下来的比赛中受到惩罚,这是永远的。这被正式定义为“冷酷触发”策略,即只要之前阶段的所有结果都描述了相互合作,就进行合作,否则就背叛。之所以这样称呼,是因为一旦扣动扳机,就没有回头路了。
这种策略应该建立起长期合作的均衡路径。然而,它并不能完全防止玩家偏离,因为自私的玩家自然会倾向于采取近视偏离,即在舞台游戏中玩偏离。这种偏差是必然存在的,这实际上是合作选择首先不是局部纳什均衡的原因。但是,如果该玩家也认为其他玩家正在采取严峻的触发策略,那么该玩家预计近视偏差对当前阶段有利,但也将导致未来收益减少。因此,只要永远合作的效用高于现在采取自私的偏差并在未来面临永恒的惩罚,那么严峻的触发器就会有效。
值得注意的是,这和以前一样取决于奖励和惩罚之间的差异以及折扣因子的值。如果d低,即使是永恒惩罚的威胁似乎也不可信——这也很可能适用于宗教假设下的伦理结论。从博弈论练习的更普通的角度来看,这意味着通常要求
归结为计算最小值d建立合作,这意味着折扣因子必须落入一个区间,如(d分钟,1)有合作。
除了在合作和背叛之间进行简单选择的标准案例之外,只要有比永久背叛更严厉的惩罚,就可以创建更复杂的案例。确实,永远背叛似乎已经足够可怕,但可能会有立即惩罚和永远背叛之类的东西。这导致要求更低d建立合作关系。为了更好地理解原因,请考虑以下再次脱离道德的示例。社会合作规则一般是通过威胁惩罚来建立的。惩罚越直接或越强,合作就越好。如果您希望一个社会表现良好,例如,不通过环境污染导致全球变暖,您可以声称这将导致地球永远的破坏。不幸的是,对于预期寿命较低的婴儿潮一代来说,这种对地球的永恒破坏似乎并不十分危险,因此他们不太关心是否要将污染的地球留给他们的孙子孙女。因此,除此之外建立额外的惩罚,例如将他们送进监狱或让他们支付大量金钱可能会更有效。
由于弗里德曼定理,上述推理实际上也可以扩展到不仅获得公正合作而且获得更内卷的结果的方向。简而言之,该定理指出,如果折扣因子足够高,则玩家互动无限多轮的场景可以被驱动为满足特定条件的任何线性策略组合。条件自然是所有参与者的所得收益在帕累托意义上必须更好一世.和.,和l和米和n吨−在一世s和比舞台游戏NE的收益。很明显,要说服玩家坚持一种比 NE 奖励永远更差的策略是不可能的:在这一点上,玩家会偏离并永远玩 NE。但是,任何移动的线性组合和在和n这在和rs在bs和q在和n吨米在l吨一世pl和r这在nds这导致所有参与者的预期收益高于 NE 是可持续的,只要d足够高。该定理本质上将上述严峻触发的推理推广到目标不是进行基本合作,而是可能在多轮中混合策略和/或不同策略的情况。

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。