The next big theorem is called the intermediate value theorem and the following picture illustrates its conclusion. It gives the existence of a certain point. This theorem is due to Bolzano around 1817 . He identified completeness of $\mathbb{R}$ as the reason for its validity.
You see in the picture there is a horizontal line, $y=c$ and a continuous function which starts off less than $c$ at the point $a$ and ends up greater than $c$ at point $b$. The intermediate value theorem says there is some point between $a$ and $b$ shown in the picture as $z$ such that the value of the function at this point equals $c$. It may seem this is obvious but without completeness the conclusion of the theorem cannot be drawn. Nevertheless, the above picture makes this theorem very easy to believe. Here is a useful lemma.
Lemma 6.4.1 If $f$ is continuous on the closed interval $[a, b]$ and for some $x \in$ $[a, b], f(x) \neq c$, then there exists $\delta>0$ such that for $y \in[a, b] \cap(x-\delta, x+\delta)$, the sign of $f(y)-c$ is constant. That is, it is either always positive or always negative depending on the sign of $f(x)-c$.
Proof: Let $\varepsilon=|f(x)-c|>0$ by assumption. Then let $\delta$ correspond to this $\varepsilon$ in the definition of continuity.
Case 1: $f(x)-c>0 .$ Then for $y \in[a, b] \cap(x-\delta, x+\delta), f(x)-f(y)<f(x)-c$ and so $0<f(y)-c$.
Case 2: $f(x)-c<0 .$ Then for $y \in[a, b] \cap(x-\delta, x+\delta), f(y)-f(x)f(y)-c$.
Next here is a proof of the intermediate value theorem.
Theorem 6.4.2 Suppose $f:[a, b] \rightarrow \mathbb{R}$ is continuous and suppose $f(a)<c<$ $f(b)$. Then there exists $x \in(a, b)$ such that $f(x)=c$.
Proof: Let $d=\frac{a+b}{2}$ and consider the intervals $[a, d]$ and $[d, b]$. If $f(d) \geq c$, then on $[a, d]$, the function is $\leq c$ at one end point and $\geq c$ at the other. On the other hand, if $f(d) \leq c$, then on $[d, b], f \geq 0$ at one end point and $\leq 0$ at the other. Pick the interval on which $f$ has values which are at least as large as $c$ and values no larger than $c$. Now consider that interval, divide it in half as was done for the original interval and argue
that on one of these smaller intervals, the function has values at least as large as $c$ and values no larger than $c$. Continue in this way. Next apply the nested interval lemma to get $x$ in all these intervals. In the $n^{\text {th }}$ interval, let $x_{n}, y_{n}$ be points of this interval such that $f\left(x_{n}\right) \leq c, f\left(y_{n}\right) \geq c$. Now $\left|x_{n}-x\right| \leq(b-a) 2^{-n}$ and $\left|y_{n}-x\right| \leq(b-a) 2^{-n}$ and so $x_{n} \rightarrow x$ and $y_{n} \rightarrow x$. Therefore, from Theorem $6.1 .1$ and limit theorems for sequences, Theorem 4.4.13,
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(x{n}\right)-c\right) \leq 0
$$
while
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(y{n}\right)-c\right) \geq 0 .
$$
Consequently $f(x)=c$ and this proves the theorem.
Here is another proof of this major theorem.
Proof: Since $f(a)<c$, the set, $S$ defined as
$$
S \equiv{x \in[a, b]: f(t) \leq c \text { for all } t \in[a, x]}
$$
is nonempty. In particular $a \in S$. Note that $b \notin S$ by assumption. Let $z \equiv \sup (S)$. By Lemma 6.4.1, since $f(a)<c$ it follows that $z \in(a, b)$. By the same lemma again, if $f(z) \neq c$, then $z \neq \sup (S)$. Hence $f(z)=c$.
Lemma 6.4.3 Let $\phi:[a, b] \rightarrow \mathbb{R}$ be a continuous function and suppose $\phi$ is $1-1$ on $(a, b)$. Then $\phi$ is either strictly increasing or strictly decreasing on $[a, b]$.
Proof: First it is shown that $\phi$ is either strictly increasing or strictly decreasing on $(a, b)$.
If $\phi$ is not strictly decreasing on $(a, b)$, then there exists $x_{1}0
$$
If for some other pair of points, $x_{2}0$, there exists $t \in(0,1)$ such that $h(t)=0 .$ Therefore, both $x_{t}$ and $y_{t}$ are points of $(a, b)$ and $\phi\left(y_{t}\right)-\phi\left(x_{t}\right)=0$ contradicting the assumption that $\phi$ is one to one. It follows $\phi$ is either strictly increasing or strictly decreasing on $(a, b)$.
This property of being either strictly increasing or strictly decreasing on $(a, b)$ carries over to $[a, b]$ by the continuity of $\phi$. Suppose $\phi$ is strictly increasing on $(a, b)$. (A similar argument holds for $\phi$ strictly decreasing on $(a, b)$.) If $x>a$, then let $z_{n}$ be a decreasing sequence of points of $(a, x)$ converging to $a$. Then by continuity of $\phi$ at $a$,
$$
\phi(a)=\lim {n \rightarrow \infty} \phi\left(z{n}\right) \leq \phi\left(z_{1}\right)<\phi(x) . $$ Therefore, $\phi(a)<\phi(x)$ whenever $x \in(a, b)$. Similarly $\phi(b)>\phi(x)$ for all $x \in(a, b)$.
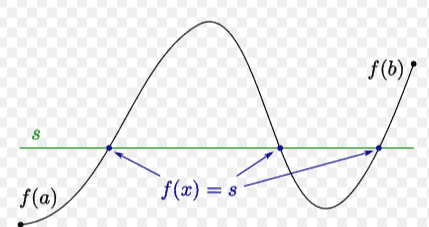
下一个大定理称为中间值定理,下图说明了它的结论。它给出了某个点的存在。这个定理是由于博尔扎诺在 1817 年左右提出的。他认为 $\mathbb{R}$ 的完整性是其有效性的原因。
您在图片中看到有一条水平线,$y=c$ 和一个连续函数,它在点 $a$ 处开始小于 $c$,并在点 $b$ 处大于 $c$。中间值定理表示在图中 $z$ 所示的 $a$ 和 $b$ 之间存在某个点,使得该点的函数值等于 $c$。这似乎是显而易见的,但如果不完整,就无法得出定理的结论。然而,上面的图片使这个定理很容易相信。这是一个有用的引理。
引理 6.4.1 如果 $f$ 在闭区间 $[a, b]$ 上是连续的并且对于某个 $x \in$ $[a, b], f(x) \neq c$,则存在 $\ delta>0$ 使得对于 $y \in[a, b] \cap(x-\delta, x+\delta)$,$f(y)-c$ 的符号是恒定的。也就是说,它要么总是正的,要么总是负的,这取决于 $f(x)-c$ 的符号。
证明:假设 $\varepsilon=|f(x)-c|>0$。然后让$\delta$ 对应于连续性定义中的这个$\varepsilon$。
情况 1:$f(x)-c>0 .$ 那么对于 $y \in[a, b] \cap(x-\delta, x+\delta), f(x)-f(y)<f( x)-c$ 等 $0<f(y)-c$。
情况 2:$f(x)-c<0 .$ 那么对于 $y \in[a, b] \cap(x-\delta, x+\delta), f(y)-f(x)f(y)-c$。
接下来是中间值定理的证明。
定理 6.4.2 假设 $f:[a, b] \rightarrow \mathbb{R}$ 是连续的并且假设 $f(a)<c<$ $f(b)$。那么存在$x \in(a, b)$ 使得$f(x)=c$。
证明:令 $d=\frac{a+b}{2}$ 并考虑区间 $[a, d]$ 和 $[d, b]$。如果$f(d) \geq c$,那么在$[a, d]$上,函数在一个端点是$\leq c$,在另一个端点是$\geq c$。另一方面,如果$f(d) \leq c$,那么在$[d, b] 上,f \geq 0$ 在一个端点,$\leq 0$ 在另一个端点。选择 $f$ 的值至少与 $c$ 一样大且值不大于 $c$ 的区间。现在考虑那个区间,像原来的区间一样把它分成两半,然后争论
在这些较小的间隔之一上,该函数的值至少与 $c$ 一样大,并且值不大于 $c$。以这种方式继续。接下来应用嵌套间隔引理在所有这些间隔中得到 $x$。在 $n^{\text {th }}$ 区间中,设 $x_{n}, y_{n}$ 为该区间的点使得 $f\left(x_{n}\right) \leq c, f\left(y_{n}\right) \geq c$。现在 $\left|x_{n}-x\right| \leq(b-a) 2^{-n}$ 和 $\left|y_{n}-x\right| \leq(b-a) 2^{-n}$ 等 $x_{n} \rightarrow x$ 和 $y_{n} \rightarrow x$。因此,从定理 $6.1 .1$ 和序列的极限定理,定理 4.4.13,
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(x{n}\right)-c\right) \leq 0
$$
尽管
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(y{n}\right)-c\right) \geq 0 。
$$
因此 $f(x)=c$ 并且这证明了定理。
这是这个大定理的另一个证明。
证明:由于$f(a)<c$,集合$S$定义为
$$
S \equiv{x \in[a, b]: f(t) \leq c \text { 对于所有 } t \in[a, x]}
$$
是非空的。特别是 $a \in S$。请注意 $b \notin S$ 假设。设 $z \equiv \sup (S)$。根据引理 6.4.1,由于 $f(a)<c$,因此 $z \in(a, b)$。再次由同样的引理,如果 $f(z) \neq c$,那么 $z \neq \sup (S)$。因此$f(z)=c$。
引理 6.4.3 令 $\phi:[a, b] \rightarrow \mathbb{R}$ 是一个连续函数并且假设 $\phi$ 在 $(a, b)$ 上是 $1-1$。那么$\phi$ 在$[a, b]$ 上要么严格递增,要么严格递减。
证明:首先证明$\phi$ 在$(a, b)$ 上要么严格递增,要么严格递减。
如果 $\phi$ 在 $(a, b)$ 上不是严格递减的,则存在 $x_{1}0
$$
如果对于其他一些点,$x_{2}0$,存在$t\in(0,1)$使得$h(t)=0.$因此, $x_{t}$ 和 $y_{t}$ 都是 $(a, b)$ 和 $\phi\left(y_{t}\right)-\phi\left(x_{t}\对)=0$ 与 $\phi$ 是一对一的假设相矛盾。它遵循 $\phi$ 在 $(a, b)$ 上要么严格增加,要么严格减少。
这种严格递增或严格递减的性质

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。