$5.5$ Double Series
Sometimes it is required to consider double series which are of the form
$$
\sum_{k=m}^{\infty} \sum_{j=m}^{\infty} a_{j k} \equiv \sum_{k=m}^{\infty}\left(\sum_{j=m}^{\infty} a_{j k}\right)
$$
In other words, first sum on $j$ yielding something which depends on $k$ and then sum these. The major consideration for these double series is the question of when
$$
\sum_{k=m}^{\infty} \sum_{j=m}^{\infty} a_{j k}=\sum_{j=m}^{\infty} \sum_{k=m}^{\infty} a_{j k}
$$
In other words, when does it make no difference which subscript is summed over first? In the case of finite sums there is no issue here. You can always write
$$
\sum_{k=m}^{M} \sum_{j=m}^{N} a_{j k}=\sum_{j=m}^{N} \sum_{k=m}^{M} a_{j k}
$$
because addition is commutative. However, there are limits involved with infinite sums and the interchange in order of summation involves taking limits in a different order. Therefore, it is not always true that it is permissible to interchange the two sums. A general rule of thumb is this: If something involves changing the order in which two limits are taken, you may not do it without agonizing over the question. In general, limits foul up algebra and also introduce things which are counter intuitive. Here is an example. This example is a little technical. It is placed here just to prove conclusively there is a question which needs to be considered.
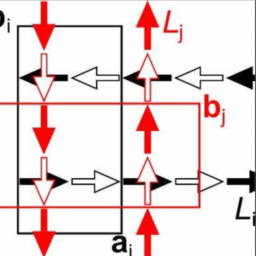
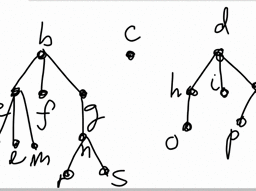
Example 5.5.1 Consider the following picture which depicts some of the ordered pairs $(m, n)$ where $m, n$ are positive integers.
The $a, b, c$ are the values of $a_{m n}$. Thus $a_{n n}=0$ for all $n \geq 1, a_{21}=a, a_{12}=b, a_{m(m+1)}=$ $-c$ whenever $m>1$, and $a_{m(m-1)}=c$ whenever $m>2$. The numbers next to the point are the values of $a_{\operatorname{mn}}$. You see $a_{n n}=0$ for all $n, a_{21}=a, a_{12}=b, a_{m n}=c$ for $(m, n)$ on the line $y=1+x$ whenever $m>1$, and $a_{m n}=-c$ for all $(m, n)$ on the line $y=x-1$ whenever $m>2$.
Then $\sum_{m-1}^{\infty} a_{m n}=a$ if $n=1, \sum_{m-1}^{\infty} a_{m n}=b-c$ if $n=2$ and if $n>2, \sum_{m-1}^{\infty} a_{m n}=$ 0. Therefore,
$$
\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} a_{m n}=a+b-c
$$
Next observe that $\sum_{n-1}^{\infty} a_{m n}=b$ if $m=1, \sum_{n-1}^{\infty} a_{m n}=a+c$ if $m=2$, and $\sum_{n-1}^{\infty} a_{m n}=$ 0 if $m>2$. Therefore,
$$
\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} a_{m n}=b+a+c
$$
and so the two sums are different. Moreover, you can see that by assigning different values of $a, b$, and $c$, you can get an example for any two different numbers desired.
Don’t become upset by this. It happens because, as indicated above, limits are taken in two different orders. An infinite sum always involves a limit and this illustrates why you must always remember this. This example in no way violates the commutative law of addition which has nothing to do with limits. Algebra is not analysis. Crazy things happen when you take limits. Intuition is routinely rendered useless.
However, it turns out that if $a_{i j} \geq 0$ for all $i, j$, then you can always interchange the order of summation. This is shown next and is based on the Lemms $2.10 .5$ which says you can intercange supremums.
Lemma $5.5 .2$ If $\left{A_{n}\right}$ is an increasing sequence in $[-\infty, \infty]$, then
$$
\sup \left{A_{n}\right}=\lim {n \rightarrow \infty} A{n-}
$$
Proof: Let sup $\left(\left{A_{n}: n \in \mathbb{N}\right}\right)=r$. In the first case, suppose $r<\infty$. Then letting $E>0$ be given, there exists $n$ such that $A_{n} \in(r-\varepsilon, r]$. Since $\left{A_{n}\right}$ is increasing, it follows if $m>n$, then $r-\varepsilon{n \rightarrow \infty} A{n}=r$ as claimed. In the case where $r=\infty$, then if $a$ is a real number, there exists $n$ such that $A_{n}>a$. Since $\left{A_{k}\right}$ is increasing, it follows that if $m>n, A_{m}>a$. But this is what is meant by $\lim {n \rightarrow \infty} A{n}=\infty$. The other case is that $r=-\infty$. But in this case, $A_{n}=-\infty$ for all $n$ and so $\lim {n \rightarrow \infty} A{n}=-\infty$.
Theorem $5.5 .3$ Let $a_{1 j} \geq 0$. Then
$$
\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} a_{i j}=\sum_{j=1}^{\infty} \sum_{i=1}^{\infty} a_{i j} .
$$
Proof: First note there is no trouble in defining these sums because the $a_{i j}$ are all nonnegative. If a sum diverges, it only diverges to $\infty$ and so $\infty$ is the value of the sum. Next note that $\sum_{j-r}^{\infty} \sum_{1-r}^{\infty} a_{i j} \geq \sup {n} \sum{j-r}^{\infty} \sum_{1-r}^{n} a_{i j}$ because for all $j, \sum_{1-r}^{\infty} a_{i j} \geq$ $\sum_{1-r}^{n} a_{1 j}$.Therefore, using Lemma 5.5.2,
$$
\begin{aligned}
&\sum_{j=r}^{\infty} \sum_{i=r}^{\infty} a_{i j} \geq \sup {n} \sum{j=r}^{\infty} \sum_{i=r}^{n} a_{i j}=\sup {n} \lim {m \rightarrow \infty} \sum_{j=r}^{m} \sum_{t=r}^{n} a_{i j} \
&=\sup {n} \lim {m \rightarrow \infty} \sum_{i=r}^{n} \sum_{j=r}^{m} a_{i j}=\sup {n} \sum{i=r}^{n} \lim {m \rightarrow \infty} \sum{j=r}^{m} a_{i j} \
&=\sup {n} \sum{i=r}^{n} \sum_{j=r}^{\infty} a_{i j}=\lim {n \rightarrow \infty} \sum{i=r}^{n} \sum_{j=r}^{\infty} a_{i j}=\sum_{i=r}^{\infty} \sum_{j=r}^{\infty} a_{i j}
\end{aligned}
$$
Interchanging the $i$ and $j$ in the above argument proves the theorem.
The following is the fundamental result on double sums.
Theorem $5.5 .4$ Let $a_{1 j} \in \mathrm{F}$ and suppose
$$
\sum_{i=r}^{\infty} \sum_{j=r}^{\infty}\left|a_{i j}\right|<\infty
$$
Then
$$
\sum_{i=r}^{\infty} \sum_{j=r}^{\infty} a_{i j}=\sum_{j=r_{i}=r}^{\infty} \sum_{i j}^{\infty} a_{i j}
$$
and every infinite sum encountered in the above equation converges.
Proof: By Theorem $5.5 .3 \sum_{j-r}^{\infty} \sum_{-r-r}^{\infty}\left|a_{1 j}\right|=\sum_{t \rightarrow r}^{\infty} \sum_{j-r}^{\infty}\left|a_{1 j}\right|<\infty$. Therefore, for each $j, \sum_{t-r}^{\infty}\left|a_{i j}\right|<\infty$ and for each $i, \sum_{j-r}^{\infty}\left|a_{i j}\right|<\infty$. By Theorem $5.2 .2$ on Page $79, \sum_{i-r}^{\infty} a_{i j}, \sum_{j-r}^{\infty} a_{i j}$ both converge, the first one for every $j$ and the second for every i. Also, $\sum_{j-r}^{\infty}\left|\sum_{i-r}^{\infty} a_{i j}\right| \leq \sum_{j-r}^{\infty} \sum_{1-r}^{\infty}\left|a_{i j}\right|<\infty$ and $\sum_{i=r}^{\infty}\left|\sum_{j-r}^{\infty} a_{i j}\right| \leq$ $\sum_{1-r}^{\infty} \sum_{j-r}^{\infty}\left|a_{i j}\right|<\infty$ so by Theorem $5.2 .2$ again, $\sum_{j=r}^{\infty} \sum_{1-r}^{\infty} a_{i j}, \sum_{1-r}^{\infty} \sum_{j-r}^{\infty} a_{i j}$ both exist. It only remains to verify they are equal. By similar reasoning you can replace $a_{i j}$ with $\operatorname{Re} a_{1 j}$ or with $\operatorname{Im} a_{1 j}$ in the above and the two sums will exist.
The real part of a finite sum of complex numbers equals the sum of the real parts. Then passing to a limit, it follows $\operatorname{Re} \sum_{j-r}^{\infty} \sum_{t \rightarrow r}^{\infty} a_{i j}=\sum_{j-r}^{\infty} \sum_{j \rightarrow r}^{\infty} \operatorname{Re} a_{i j}$ and similarly, $\operatorname{Im} \sum_{1-r}^{\infty} \sum_{j-r}^{\infty} a_{1 j}=\sum_{1-r}^{\infty} \sum_{j=r}^{\infty} \operatorname{Im} a_{1 j} .$ Note $0 \leq\left(\left|a_{1 j}\right|+\operatorname{Re} a_{1 j}\right) \leq 2\left|a_{i j}\right| .$ Therefore, by Theorem $5.5 .3$ and Theorem 5.1.5 on Page 78
$$
\sum_{j=r}^{\infty} \sum_{i=r}^{\infty}\left|a_{i j}\right|+\sum_{j=r}^{\infty} \sum_{i=r}^{\infty} \operatorname{Re} a_{i j}=\sum_{j=r}^{\infty} \sum_{i=r}^{\infty}\left(\left|a_{i j}\right|+\operatorname{Re} a_{i j}\right)
$$
$$
=\sum_{i=r}^{\infty} \sum_{j=r}^{\infty}\left(\left|a_{i j}\right|+\operatorname{Re} a_{i j}\right)=\sum_{i=r}^{\infty} \sum_{j=r}^{\infty}\left|a_{i j}\right|+\sum_{i=r}^{\infty} \sum_{j=r}^{\infty} \operatorname{Re} a_{i j}=\sum_{j=r}^{\infty} \sum_{i=r}^{\infty}\left|a_{i j}\right|+\sum_{i=r}^{\infty} \sum_{j=r}^{\infty} \operatorname{Re} a_{i j}
$$
and 30
$$
\operatorname{Re} \sum_{j=r}^{\infty} \sum_{i=r}^{\infty} a_{i j}=\sum_{j=r}^{\infty} \sum_{i=r}^{\infty} \operatorname{Re} a_{i j}=\sum_{i=r}^{\infty} \sum_{j=r}^{\infty} \operatorname{Re} a_{i j}=\operatorname{Re} \sum_{i=r}^{\infty} \sum_{j=r}^{\infty} a_{i j}
$$
Similar reasoning applies to the imaginary parts. Since the real and imaginary parts of the two series are equal, it follows the two series are equal.
One of the most important applications of this theorem is to the problem of multiplication of series.
微积分note Double Series
$5.5$ 双系列
有时需要考虑以下形式的双系列
$$
\sum_{k=m}^{\infty} \sum_{j=m}^{\infty} a_{jk} \equiv \sum_{k=m}^{\infty}\left(\sum_{j= m}^{\infty} a_{jk}\right)
$$
换句话说,首先对 $j$ 求和,产生依赖于 $k$ 的东西,然后对这些求和。这些双系列的主要考虑因素是何时
$$
\sum_{k=m}^{\infty} \sum_{j=m}^{\infty} a_{jk}=\sum_{j=m}^{\infty} \sum_{k=m}^{ \infty} a_{jk}
$$
换句话说,什么时候先求和哪个下标没有区别?在有限和的情况下,这里没有问题。你总是可以写
$$
\sum_{k=m}^{M} \sum_{j=m}^{N} a_{jk}=\sum_{j=m}^{N} \sum_{k=m}^{M} a_ {jk}
$$
因为加法是可交换的。但是,无限和存在限制,并且求和顺序的交换涉及以不同的顺序取限制。因此,允许互换这两个总和并不总是正确的。一般的经验法则是:如果某件事涉及改变两个限制的顺序,你可能不会在不为这个问题苦恼的情况下做这件事。一般来说,限制会破坏代数并引入一些违反直觉的东西。这是一个例子。这个例子有点技术性。放在这里只是为了最终证明有一个需要考虑的问题。
例 5.5.1 考虑下图,它描述了一些有序对 $(m, n)$ 其中 $m, n$ 是正整数。
$a, b, c$ 是 $a_{m n}$ 的值。因此 $a_{nn}=0$ 对于所有 $n \geq 1, a_{21}=a, a_{12}=b, a_{m(m+1)}=$ $-c$ 每当 $m> 1$,并且只要 $m>2$,$a_{m(m-1)}=c$。该点旁边的数字是 $a_{\operatorname{mn}}$ 的值。你看到 $a_{nn}=0$ for all $n, a_{21}=a, a_{12}=b, a_{mn}=c$ for $(m, n)$ on the line $y= 1+x$ 每当 $m>1$ 时,$a_{mn}=-c$ 对于行 $y=x-1$ 上的所有 $(m, n)$ 每当 $m>2$ 时。
那么 $\sum_{m-1}^{\infty} a_{mn}=a$ 如果 $n=1, \sum_{m-1}^{\infty} a_{mn}=bc$ 如果 $n= 2$,如果 $n>2,\sum_{m-1}^{\infty} a_{mn}=$ 0。因此,
$$
\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} a_{m n}=a+b-c
$$
接下来观察 $\sum_{n-1}^{\infty} a_{mn}=b$ if $m=1, \sum_{n-1}^{\infty} a_{mn}=a+c$如果 $m=2$,如果 $m>2$,则 $\sum_{n-1}^{\infty} a_{mn}=$ 0。所以,
$$
\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} a_{m n}=b+a+c
$$
所以这两个总和是不同的。此外,您可以看到,通过分配 $a、b$ 和 $c$ 的不同值,您可以获得所需的任意两个不同数字的示例。
不要因此而心烦意乱。发生这种情况是因为,如上所述,限制采用两种不同的顺序。无限和总是包含一个限制,这说明了为什么你必须始终记住这一点。这个例子绝不违反与极限无关的加法交换律。代数不是分析。当你采取限制措施时,就会发生疯狂的事情。直觉通常变得无用。
然而,事实证明,如果 $a_{i j} \geq 0$ 对于所有 $i, j$,那么你总是可以互换求和的顺序。下面显示了它,它基于 Lemms $2.10 .5$,它说你可以互换 supremums。
引理 $5.5 .2$ 如果 $\left{A_{n}\right}$ 是 $[-\infty, \infty]$ 中的递增序列,则
$$
\sup \left{A_{n}\right}=\lim {n \rightarrow \infty} A{n-}
$$
证明:设$\left(\left{A_{n}: n \in \mathbb{N}\right}\right)=r$。在第一种情况下,假设 $r<\infty$。然后让 $E>0$ 给定,存在 $n$ 使得 $A_{n} \in(r-\varepsilon, r]$。因为 $\left{A_{n}\right}$ 是增加,如果 $m>n$,那么 $r-\varepsilon{n \rightarrow \infty} A{n}= r$ 如所声称的。在 $r=\infty$ 的情况下,如果 $a$ 是实数,则存在 $n$ 使得 $A_{n}>a$。由于 $\left{A_{ k}\right}$ 正在增加,因此如果 $m>n,A_{m}>a$。但这就是 $\lim {n \rightarrow \infty} A{n}= 的意思\infty$。另一种情况是 $r=-\infty$。但在这种情况下,对于所有 $n$,$A_{n}=-\infty$ 等 $\lim {n \rightarrow \infty} A{n}=-\infty$。
定理 $5.5 .3$ 令 $a_{1 j} \geq 0$。然后
$$
\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} a_{ij}=\sum_{j=1}^{\infty} \sum_{i=1}^{ \infty} a_{ij} 。
$$
证明:首先注意定义这些和没有问题,因为 $a_{i j}$ 都是非负的。如果总和发散,它只会发散到 $\infty$,因此 $\infty$ 是总和的值。接下来注意 $\sum_{jr}^{\infty} \sum_{1-r}^{\infty} a_{ij} \geq \sup {n} \sum{jr}^{\infty} \sum_ {1-r}^{n} a_{ij}$ 因为对于所有 $j,\sum_{1-r}^{\infty} a_{ij} \geq$ $\sum_{1-r}^{n } a_{1 j}$.因此,使用引理 5.5.2,
$$
\开始{对齐}
&\sum_{j=r}^{\infty} \sum_{i=r}^{\infty} a_{ij} \geq \sup {n} \sum{j=r}^{\infty} \ sum_{i=r}^{n} a_{ij}=\sup {n} \lim {m \rightarrow \infty} \sum_{j=r}^{m} \sum_{t=r}^ {n} a_{ij} \
&=\sup {n} \lim {m \rightarrow \infty} \sum_{i=r}^{n} \sum_{j=r}^{m} a_{ij}=\sup {n } \sum{i=r}^{n} \lim {m \rightarrow \infty} \sum{

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。